| [38] Sirpi | 2004-05-05 11:03:18 |
 A feladat kapcsán felmerült bennem, hogy általánosan mit lehet a problémáról mondani. Legyen adva n: az egy sorban levő mezők száma, valamint k: a felhasznált színek száma. Ekkor a kérdés az, hogy legalább hány sorra van szükség, hogy legyen olyan rácstéglalap, melynek csúcsai egyszinűek.
A feladatnak akkor van értelme, ha n legalább 3 és k legalább 2. Konkrét esetekre meg lehet oldani számítógéppel a feladatot, de pillanatnyilag csak lassú módszert tudok: csináljunk egy gráfot, melynek elemei a lehetséges sorok - ekkor a gráfnak kn pontja lesz - és kössünk össze két pontot, ha együtt nem alkot semelyik 4 pontjuk egyszínű téglalapot. Ebben a gráfban kell klikket keresni, azaz maximális teljes részgráfot (erre nem ismeretes gyors algoritmus). A maximális klikk méreténél eggyel több sort véve mindenképpen lesz téglalap.
Persze, amit leírtam, nem garantálja, hogy a feladat megoldhatatlan, ugyanis a gráf elég speciális szerkezetű, elképzelhető, hogy meg lehet adni explicite a maximális klikk méretét k és n függvényében (bár nem biztos, hogy ez megy, lehet, hogy csak kétoldali nagyságrendi becslélt lehet adni...)
Ha valaki jut valamire, ne tartsa vissza (bár még szívesen töröm a fejem a problémán)
Sirpi
|
|
|
|
|
|
| [33] enel | 2004-05-04 17:47:44 |
 Lanyom neveben, ket feladat, aminek "surgosen" kellene a megoldasa.
Kivalasztunk 300 racspontot ugy, hogy 1 <= x <= 10, 1 <= y <= 30. Mindegyiknek van szine,piros, kek vagy zold. Bizonyitando, hogy van olyan teglalap, amely a tengelyekkel parhuzamos es azonos szinu negy pont.
Egy tarsasagban mindenkinek van legalabb 9 ismerose, az ismeretseg kolcsonos. Bizonyitando, hogy kivalaszthato legalabb 10 ember ugy, hogy azok leultethetok egy asztal kore es mindenki ismeri a ket szomszedjat.
|
|
| [32] Csimby | 2004-04-30 15:36:09 |
 Bocsánat [28]-ban elszúrtam a példát. Helyesen:
Pl.: a=0,09191919...; b=0,019191919... a és b összefűzve: 0,0019191919...
Géza kérdésén gondolkodom...
|
| Előzmény: [28] Csimby, 2004-04-27 23:03:06 |
|
|
| [30] Csimby | 2004-04-29 22:37:29 |
 Valami olyasmit ami két valós számhoz egy-egyértelműen hozzárendel egy harmadikat (úgy, hogy így minden valós számot megkapjunk). Lehet, hogy nincs, de én nem látom, hogy miért. Amit [28]-ban írtam az ezt műveli az egészekkel (ott x,y egész).
|
| Előzmény: [29] Pach Péter Pál, 2004-04-27 23:27:06 |
|
|
| [28] Csimby | 2004-04-27 23:03:06 |
 Kedves Géza és Lajos!
Ez a módszer kijavítható a következő képpen: Ha 9-es jegy szerepel valamelyik számban, akkor a következő 9-esig alkossanak egy "egység"-et a jegyek és így "fűzzük" össze a két számot. Pl.: a=0,09191919...; b=0,019191919... a és b összefűzve: 0,019191919... Ekkor 0,909090... szétbontva: a=b=0,909090... Ha jól sejtem ez általánosítható sík és egyenes pontjai közötti megfeleltetésnek is(?).
De nincsen vmi olyasmi a valós számokra mint pl. ez az egész számokra: f(x,y)=(x+y-1)(x+y-2)/2+y
Feladat: Biz. be, hogy f(x,y) kölcsönösen egyértelmű és az egész számok teljes halmazára képez le.
|
|
|
| [26] Lóczi Lajos | 2004-04-27 01:31:03 |
 Kedves Csimby!
Természetesen egyszerűen is meg lehet adni bijekciót a sík és az egyenes pontjai között, pl. az ún. összefésülési eljárással. Lustaságból csak bemásolok ide valamit, amit a neten találtam, remélem, nem baj, hogy angolul van.
"...there is a bijection between R and RxR, which means that the real line and the plane "have the same number of points". Here is one such bijection: interleave the digits of the two real numbers that make up an element of RxR, and you will get a real number (an element of R). Conversely, given any real number in R, I can turn it into an element of RxR by pulling out alternating digits and constructing two real numbers from them. To every point in R there corresponds one and only one point of RxR using this interleaving, so there are the same "number" of elements in R as there are in RxR.
Example of interleaving:
Given the element (0.1532,0.5438) of RxR, I can convert it into the element 0.15543328 of R; given the element 0.2854325710 of R, I can convert it into the element (0.25351,0.84270) of RxR."
A fenti leírást azzal a finomítással egészíteném ki, hogy az "ismétlődő 9-esek problémáját" még ki kell küszöbölni benne; ismert, hogy a valós számok tizedestört-alakja bizonyos esetekben nem egyértelmű, pl. 0.99999...=1.00000... . Így pl. állapodjunk meg, hogy az összefésülésnél mindig a 2. alakot használjuk, azaz sosem írunk végtelen sok 9-est egymás mellé egy valós szám tizedestört-kifejtésében. Ha ezt nem tennénk, a fenti összefésülésben baj keletkezne: pl. a (0.9999...,0.000...)=(1.000...,0.000...) síkbeli pontnak a tizedestört-kifejtéstől függően két különböző képe lenne: (0.90909...) vagy (1,000...).
|
| Előzmény: [24] Csimby, 2004-04-23 19:41:31 |
|
| [25] lorantfy | 2004-04-23 23:48:09 |
 Kedves Levente és Fórumosok!
A "halálraitélt problémáját" az Érdmatfel. témában Gyuri adta fel a [133] hozzászólásban és a köv. hozzászólásokban foglalkoztunk még vele [143,153,157,158,159,170,172,175].
Annyi az eltérés az általad említetthez képest, hogy a büntetést a következő hét valamelyik napján reggel 8-kor hajtják végre és a halálraitélt legkorábban aznap reggel 6 órakor tudhatja meg, hogy kivégzik. Ha előbb megtudja, akkor nem végezhetik ki. Fontosak ezek a részletek, mert ettől lesz a probléma megoldhatatlan.
Ugyanis nem mondják meg neki 6-kor, hogy aznap 8-kor kivégzik, így aztán 8 óra előtt egy végtelen következtetési verembe esik, hiszen tudja, hogy ma fogják kivégezni, de nem jönnek kivégezni, mert tudják, hogy tudja, tehát nem is ma fogják kivégezni, akkor viszont rosszult tudja, ha viszont nem tudja biztosan, hogy ma fogják kivégezni, akkor akár ki is végezhetik a mai napon...
A hozzászólók szerint ez egy gödeli probléma. Én nem ismertem, igy rákerestem. A lényeget egy kis példával ide másolom:
A Gödel-tétel az első olyan felfedezés a logika történetében, amelyen Arisztotelész komolyan meglepődne, és kénytelen lenne egész gondolati rendszerét átszervezni. Az 1931-ben felfedezett tétel azt bizonyítja, hogy ha egy matematikai rendszerben minden igaz állítás bizonyítható, akkor a rendszer szükségszerűen ellentmondásos. Más szavakkal: ha egy formális rendszer ellentmondásmentes, akkor megfogalmazható olyan állítás, amely a rendszeren belül nem dönthető el, ehhez a vonatkoztatási rendszer megváltoztatása szükséges. A tétel többek közt azt is kifejezi, hogy ugyan a matematika az egyes természettudományok metaszintje, de mindegyiknek némileg más matematikára van szüksége. (Drótos László: Informatika Jegyzetek)
Kurt Gödel nevét nem sokan ismerik, pedig az ő életműve a matematikai logikában legalább olyan jelentős, mint Einsteiné a fizikában. Gödel, egy rendkívül tekintélyes matematikai logikus ugyanis a logika eszközeivel bizonyította be, hogy a logika valójában egy tökéletlen rendszer. Bár többnyire úgy emlegetik, mint egy tétel lefektetőjét, fontos megjegyeznünk, hogy valójában két tételt alkotott meg, de ebből az elsőt szokták gyakrabban idézni. Gödel első tétele így hangzik: “Egy deduktív következtetéseken alapuló rendszer, amiben lehetséges egyszerűbb aritmetikát létrehozni, vagy inkonzisztens, vagy nem teljes.” Ez a következtetés, paradox módon, pontosan a logikán belül lett bebizonyítva, amelyre (többek között) igaz ez a megállapítás. Ebből a megállapításból az következik, hogy hacsak egy rendszer nem tartalmaz ellentmondást, vagyis konzisztens, kell lennie benne egy olyan állításnak, amiről rendszeren belül nem lehet eldönteni, hogy igaz-e.
Na de vizsgáljuk csak meg, hogy mit is jelent az, hogy “nem lehet eldönteni”! Ez nem annyira egyértelmű, hiszen a mindennapi életben nem ehhez szoktunk hozzá. De nézzük csak a következő mondatot:
Ebben a mondatba harom hiba van.
Egy egyszerű, alig néhány bővítménnyel bíró mondattal állunk szemben itt. De nézzük csak meg jobban. A hibák itt vannak, ez világos! A “mondatba” szónál a helyhatározó ragot helytelenül használtuk, és a “harom” szónál hiányzik egy ékezet. Hoppá, de ez csak két hiba! Tehát ez a mondat nem igaz. Na de álljunk csak meg! Nem lehet-e, hogy ennek a mondatnak éppen az a harmadik hibája, hogy nem igaz? Akkor viszont a mondat igaz lesz! Most akkor, ha igaz, akkor mégsem lehet, hogy nem igaz, ha pedig nem igaz, akkor meg az sem lehet, hogy igaz az állítás. Belekerültünk egy gödeli csapdába. Merre tovább? Akkor most ez a mondat eldöntetlenül marad? De hát az nem lehet! Viszont ettől nem is kell félni. Hiszen csak azt mondtuk, hogy a gödeli állítás nem egyáltalán nem, hanem csak rendszeren belül nem eldönthető. Mi a megoldás? Rendszert kell váltani. Változtassuk csak meg úgy rendszert, hogy ez ne fordulhasson elő. Például mondjuk azt, hogy a mondatok igazságtartalma nem számít ebben a rendszerben hibának. Így az “Ebben a mondatba harom hiba van” mondatról könnyűszerrel kideríthető, hogy hamis állítás, hiszen a mondat csak két hibával bír. Most minden szép és jó, hiszen a rendszert felvérteztük ez ellen a csapda ellen. De ebben az új rendszerben is találhatunk olyan állítást, ami ugyanígy nem dönthető el rendszeren belül. (Kálecz Orsolya dolgozatából)
|
| Előzmény: [23] klevente, 2004-04-23 17:54:44 |
|
| [24] Csimby | 2004-04-23 19:41:31 |
 Kedves Lajos! Amit ismerek megfeleltetést az csak ilyen "okoskodás" (az egységnégyzetnek megfeleltethetjük a síkot, az egységnégyzetet megfeleltethetjük az egység hosszú szakasznak, az egység hosszú szakaszt pedig az egyenesnek). A kérdésem az lett volna, hogy tud-e valaki olyan függvényt mondani, ami szintén megfeleltet minden (x,y) valós számpárnak egy z valós számot (abból a megfeleltetésből amit ismerek és nagy vonalakban leírtam elég bonyolult lenne függvényt csinálni).
|
| Előzmény: [22] Lóczi Lajos, 2004-04-23 15:58:52 |
|
| [23] klevente | 2004-04-23 17:54:44 |
 Tiszteletem minden Fórum-lakónak. Egy januári cikk miatt keveredtem ide, ami sajnos a neten nincs fent. Dósa Tibor írt egy érdekeset néhány paradoxonról, talán sokan emlékeznek rá. Az írás néhány megállapításával szemben szeretnék ellenvetéseket tenni. Nem használnám a "cáfolni" kifejezést, hiszen ezekben a rafinált problémákban nem állíthatom, hogy magam teljesen tisztán látnék. Viszont nagyon piszkál a dolog, és igencsak szeretnék tisztán látni, s itt nálam bölcsebbektől remélek hozzászólásokat.
Emlékeztetőül: először a váratlan kivégzés paradoxonáról ír. A halálraítéltről elrendelik, hogy a következő hét valamelyik napján VÁRATLANUL kell végrehajtani rajta az ítéletet. Ügyvédje szerint így ha a hét utolsó napja előtti estén még életben van, akkor utolsó nap már nem végezhetik ki, mert akkor az már nem lenne váratlan. Ezek szerint legkésőbb utolsó előtti nap ki kell végezni. Stb... ezt a gondolatmenetet folytatva kapjuk, hogy egyáltalán nem végezhetik ki az illetőt.
Ha jól értem, ezt azzal oldja fel a cikkíró, hogy „a nap nem tudása” még nem jelent váratlanságot. Elismeri tehát, hogy az elítélt nem tudja a kivégzés napját. Ezzel máris feloldatlan marad a paradoxon, ha úgy kezdjük a történetet, hogy "a jövő héten valamikor kivégezzük, de Ön annyira nagy bűnt követett el, hogy - kínjait növelendő - előző este még nem tudhatja, ha másnap reggel kivégzik". Egyértelmű, hogy vasárnap nem végezhetik ki, ha ígéretüket betartják, hiszen akkor szombat este már tudná, hogy másnap kivégzik. Stb... Mégis, ha a hét közepe felé valamikor elviszik kivégezni, nem állíthatja, hogy előző este már tudta, hogy másnap hajnalban kivégzés vár rá.
Nézzünk egy másik érdekes játékot, ami mintha az előbbi paradoxonnal logikailag ekvivalens lenne. Közismert az ún. "Egyszámjáték". Most nem erről van szó, csak majdnem, kicsit ugyanis módosítsuk a szabályait. Tetszőleges nagyságú csoportban játszható. Mindenki gondol egy pozitív egész számot, maximum a 100-at. Az nyer, aki a második legnagyobbat gondolta (és nem kell, hogy ezzel egyedül legyen). Ha csupa tökéletesen gondolkodó játékost tételezünk fel, akkor a 100-ra senki nem gondol. De ha ez így van, akkor nyilván a 99-cel sem lehet nyerni, tehát arra sem gondol senki. Stb... Elvileg senkinek semmire nem szabadna gondolni. Gyakorlatban kipróbálva mi történik (ha szerencsénk van, és nincsenek játékrontók)? Kb. 92-95 közti számmal megnyeri valaki a játékot, amely problémamentesen működik. Ha több menetet játszunk egymás után, érdemes megfigyelni a győztes szám "mozgását".
Mindkét példában valamilyen értelemben a "másodikat" kerestük. Ha mindenki "második" akar lenni és "első" senki, akkor elvileg a játék (a kivégzés) nem működhet. Gyakorlatilag mégis működik, mégis kivégzik az elítéltet. MIÉRT?
Az én magyarázatom az, hogy a hibátlan logikus gondolkodás az emberi pszichén a 4-5. lépés körül egyszerűen megbicsaklik. A gyakorlatban már nem éljük át annak a súlyát, hogy "a 94-re ostobaság gondolni, hiszen 95-öt senki nem gondol" úgy, mint ahogy a 99-re valóban ostobaság, mert 100-at tényleg senki nem fog mondani. A gyakorlatban már nem éljük át annak a súlyát, hogy "ha szerda estig nem végeztek ki, akkor nyert ügyem van, hiszen csütörtökön már úgysem végezhetnek ki" úgy, mint ahogy szombat este valóban nyert ügye lenne, mert vasárnap nem végezhetnék ki.
Őszintén szólva érzem, nem biztos, hogy ezzel minden problémánk megoldódik, hiszen ha tudja, hogy vasárnap kivégzik, ezért nem végezhetik ki, akkor mégsem jól tudta, hogy kivégzik; ha pedig nem tudta, akkor mégis kivégezhetik. De a cikkben adott magyarázat sem megnyugtató.
Még egy hasonló jellegű probléma, amit 1-2 évvel ezelőtt egy Varga Tamás versenyen is kitűztek. 25 oroszlán ül egy darab hús körül. Ha bármelyik oroszlán megeszi a húst, elnehezül és maga válik a kör közepén a többiek potenciális áldozatává. Az oroszlánok jobban féltik az életüket, mint amilyen éhesek. Mi történik?
A hivatalos megoldás szerint ha csak 1 oroszlán lenne, az nyugodtan megehetné a húst. Két oroszlán esetén ha egyikük megenné a húst, akkor előállna az előző helyzet, amikor őt meg lehetne enni, tehát semmi nem történik. Három oroszlán esetén ha egyikük megenné a húst, előáll az előző helyzet... ezt folytatva kapjuk, hogy páratlan számú oroszlán esetén meg szabad enni a húst, mert páros számú oroszlánnal semmi nem történik - tehát mind a 25 ráront az élelemre. Szerintem ezzel is az a súlyos probléma, hogy míg 2-3-4 oroszlán esetén a megoldásként adott gondolatmenet teljesen rendben van, 25-nél már pszichésen annyira gyenge az érvelés, ami miatt nagyon sok vitát okozott annak idején a feladat, és végülis szerencsétlen volt a kitűzése.
Talán érdemes a felvetett kérdéseket még továbbgondolni, remélem, ezekkel a sorokkal hozzájárultam ehhez.
Koncz Levente (Bp., Árpád)
|
|
| [22] Lóczi Lajos | 2004-04-23 15:58:52 |
 Kedves Csimby, nem értem a kérdésed. Ha bijektív a megfeleltetés a sík és az egyenes pontjai között, akkor a függvény (amely tehát injektív is) eleve más értékeket kell felvegyen minden pontban.
Üdv, LL
|
| Előzmény: [21] Csimby, 2004-04-21 00:01:28 |
|
| [21] Csimby | 2004-04-21 00:01:28 |
 A sík pontjait mindenféle ügyeskedésekkel meg lehet bijektíven feleltetni egy egyenes pontjainak. Kérdesen az, hogy tud-e valaki olyan kétváltozós függvény(eke)t mondani, amely mindenütt más értéket vesz fel. (ugye ekkor a sík minden P(x,y) pontjához más értéket adna ez az f(x,y) függvény és ez felelhetne meg a számegyenesen P'-nek)
|
|
| [20] Pach Péter Pál | 2004-04-09 18:20:06 |
 Kérdésem a következő:
Mely (k,l) pozitív egész számpárokra teljesül, hogy végtelen sok olyan p pozitív prímszám van, amelyre q=kp+l is prím?
Ez persze elég nehéz, de engem már az is érdekelne, ha valaki mutatna ilyen (k,l) párt, és az is, ha olyan (k,l) párt találna, amelyre p és q egyszerre csak véges sokszor lehet prím. Természetesen kikötjük, hogy (k;l)=1 és k+l páratlan.
Előre is köszönöm.
|
|
|
| [18] Gubbubu | 2004-03-14 13:24:42 |
 Kedves László!
Én is köszönöm, hogy beírtad még egyszer a CS-egyenlőtlenséget, mert most látom, hogy amitől féltem, bekövetkezett, és tényleg elírtam. Pedig kétszer megnéztem, mielőtt elküldtem.
Feladat: keressük meg a hibát Gubbubu e topikbeli előző hozzászólásában.
Mivel ez nem először fordul elő, tényleg nagyon bánt a dolog. Úgy látszik, különös tehetségem van a TEX jelei és a Times New Roman típusú betűk közt való elkeveredésben. Csak azzal mentegethetem magam, hogy nagyon késő éjjel szoktam írogatni.
Elnézést kérek mindenkitől, nyugodtan javítsatok ki, ha máskor elírok valamit, sőt meg is köszönném.
Ami az 1)-2)-3) feltételeket illeti, azok összessége tényleg ekvivalens László feltételeivel. A különbség annyi, hogy az 1) feltételem tkp. fölösleges, bár könnyebbé teszi a formális feltétel szövegesbe való átkódolását.
Üdv mindenkinek: G.
|
| Előzmény: [17] lorantfy, 2004-03-14 11:29:56 |
|
| [17] lorantfy | 2004-03-14 11:29:56 |
 Kedves Suhanc!
Most látom, hogy Gubbubu már megadta a választ, de ha már beTEXteltem felteszem én is gyökös formában:
Cauchy-egyenlőtlenség: Legyen a1,a2,…,an és b1,b2,...,bn két, valós számokból álló sorozat, ekkor
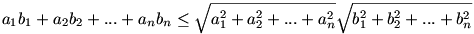
Egyenlőség csak akkor áll fenn, ha
aibj=ajbi 0 (i=1,2,...,n j=1,2,...,n) 0 (i=1,2,...,n j=1,2,...,n)
Ha bi 0(i=1,2,…,n) akkor szemléletesebben így is írható a feltétel: 0(i=1,2,…,n) akkor szemléletesebben így is írható a feltétel:
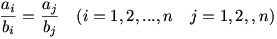
Gyakorlatilag a Gubbubu által adott 3 feltételt kapjuk.
|
| Előzmény: [13] Suhanc, 2004-03-13 19:40:58 |
|
| [16] Suhanc | 2004-03-14 10:09:29 |
 Kedves Gubbubu!
Köszönöm szépen a gyors segítséget! Igen, erre a tételre gondoltam. Én egyébként Reiman István: Matematika c. könyvében találkoztam vele... ami megtetszett, hogy közvetlenül utána a szerző e tétel segítségével vezeti le a számtani-négyzetes közép közötti egyenlőtlenséget... a suliban azt mondta a tanár, hogy ennek, illetve a szt-mértani, és mértani-harmonikus közepek közti egyenlőtlenségek általános alakjainak bizonyításai körülményesek, és rondák... (ő teljes indukciós bizonyítást említett) Ezzel pedig sokkal egyszerűbb, egyből megkapjuk az általános alakot!:)
|
|
| [15] Gubbubu | 2004-03-14 01:06:24 |
 Ja, és ha szokásomhoz híven elgépeltem volna valamit, abban az esetben, de egyébként is, érdemes átnézni Freud Róbert: Lineáris Algebra c. könyvét és/vagy Szőkefalvi-Nagy Béla: Valós függvények és függvénysorok c. könyvét, mindkettőben vannak bizonyítások is az egyenlőtlenségre. Egyébként mindkét könyv ettől függetlenül is nagyon jó.
|
| Előzmény: [14] Gubbubu, 2004-03-14 01:01:34 |
|
|
