|
|
| [3706] nadorp | 2013-04-11 16:05:24 |
 csak lusta voltam és ez már súrolja az egyetemi anyagot:-)
Ha 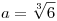 és (p,q,r) Q(a)-beli elem, akkor az inverzére és (p,q,r) Q(a)-beli elem, akkor az inverzére
(pa2+qa+r)(xa2+ya+z)=(rx+qy+pz)a2+(6px+ry+qz)a+6qx+6py+rz=1
Láthatóan egy lineáris egyenletrendszert kapunk, melynek mátrixa
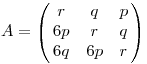 valamint jó jel, hogy |A|=36p3+6q3+r3-18pqr=1 valamint jó jel, hogy |A|=36p3+6q3+r3-18pqr=1
A szimmetria miatt ha (p,q,r) megoldása a diofantikus egyenletnek, akkor fenti egyenletrendszer x,y,z megoldása is az. Az előzőek alapján sejteni lehet, hogy ha (p,q,r) és (x,y,z) is megoldás, akkor 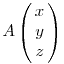 is megoldás lesz. Ez valóban így van, ezért innen indukcióval következik, hogy ha p,q,r megoldás, akkor is megoldás lesz. Ez valóban így van, ezért innen indukcióval következik, hogy ha p,q,r megoldás, akkor 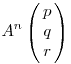 is megoldás tetszőleges n egészre ( negatív kitevő is megengedett, hiszen az A mátrix invertálható ). Innen az egyenlet megoldásai: is megoldás tetszőleges n egészre ( negatív kitevő is megengedett, hiszen az A mátrix invertálható ). Innen az egyenlet megoldásai:
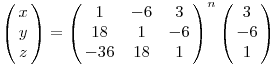
Ezt még "szebbé" lehet tenni, ha a mátrixot diagonizáljuk. Azt még nem láttam be, hogy több megoldás nincs. Ha pld. tudnánk, hogy z=1 esetén csak egy megoldás van és a rekurzió z-ben monoton, akkor ezzel is kész vagyunk.
|
| Előzmény: [3705] gyula60, 2013-04-11 13:27:06 |
|
|
|
| [3703] nadorp | 2013-04-07 10:28:50 |
 Igen, van összefüggés. Könnyű ellenőrizni, hogy tetszőleges p,q,r számokra
| (1) | p3+q3+r3-3pqr=(p+q+r)(p2+q2+r2-pq-pr-qr) |
Ezt alkalmazva a diofantikus egyenletedre, bevezetve az 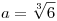 jelölést kapjuk jelölést kapjuk
36x3+6y3+z3-18xyz=(xa2+ya+z)((y2-xz)a2+(6x2-yz)a+z2-6xy)=1
Tehát, ha az egyenletnek az x,y,z számok megoldásai, akkor ez azt jelenti, hogy gyöktelenítéskor az y2-xz,6x2-yz,z2-6xy együtthatókat kell kapnunk. Esetünkben a 3,-6,1 számok kielégítik (1)-et, ezért gyöktelenítéskor a 33,60,109 együtthatókat kell, hogy kapjuk.
|
| Előzmény: [3700] gyula60, 2013-04-06 22:05:08 |
|
| [3702] w | 2013-04-07 09:18:45 |
 Próbáld meg faktorizálni. Ha k páros, a kifejezés is páros lesz, úgyhogy a páratlan k számok esete számít.
45(2k+1)+(5(2k+1))4=410k+5+(10k+5)4=...
(Már kiírtak megoldást a korábbi hozzászólásokban.)
|
| Előzmény: [3701] gyula60, 2013-04-06 23:09:43 |
|
| [3701] gyula60 | 2013-04-06 23:09:43 |
 Ha segít valamit az, hogy a számítógépem megnézte az összes 45k+(5k)4, (k=1,2,...,109) alakú számokat és false választ adott. Ebből talán felállítható egy sejtés, de a válasz nálam is meghaladja jelenlegi tudásomat.
|
| Előzmény: [3646] w, 2012-12-08 20:48:35 |
|
| [3700] gyula60 | 2013-04-06 22:05:08 |
 Szeretnék egy számelméleti problémát ismertetni:
Van-e kapcsolat a következő 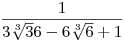 tört nevezőjének gyöktelenítése és a 36x3+6y(y2-3xz)+z3=1 háromismeretlenes diofantoszi egyenlet megoldása között, ha tudjuk, hogy a tört nevezőjének együtthatói adják az egyenlet egyik megoldását? tört nevezőjének gyöktelenítése és a 36x3+6y(y2-3xz)+z3=1 háromismeretlenes diofantoszi egyenlet megoldása között, ha tudjuk, hogy a tört nevezőjének együtthatói adják az egyenlet egyik megoldását?
|
|
|
| [3697] w | 2013-02-28 20:48:10 |
 Kicsit elbonyolítottad*: az
16(((s-b)(s-c))2+((s-c)(s-a))2+((s-a)(s-b))2) a4+b4+c4 a4+b4+c4
egyenlőtlenség AM-GM miatt nyilván igaz: pl.
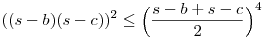 , ahol s-b+s-c=a. Innen egyenlőség esete is adódik. , ahol s-b+s-c=a. Innen egyenlőség esete is adódik.
-
*Persze ízlés kérdése, hogy teljes négyzetes alakra hozod-e.
|
| Előzmény: [3696] sakkmath, 2013-02-28 14:45:49 |
|
| [3696] sakkmath | 2013-02-28 14:45:49 |
 Használjuk fel Kiss György: Amit jó tudni a háromszögekről című cikkének eredményeit:
először az rra = (s-b)(s-c), rrb = (s-c)(s-a), rrc = (s-a)(s-b) összefüggéseket, később pedig a jól ismert, következő helyettesítéseket: s-a = x, s-b = y, s-c = z, illetve: a = y+z, b = z+x, c = x+y .
|
 |
| Előzmény: [3695] w, 2013-02-23 16:53:45 |
|
|
|
|
| [3692] w | 2013-02-21 22:08:17 |
 Köszönöm a hozzászólást, a Pedoe-egyenlőtlenséget nem ismertem, csak a Weitzenböck-öt és a Hadwiger-Finsler-t.
Egyetértek, a háromváltozós egyenlőtlenségek nem túl izgalmasak, leginkább a (még) több változós egyenlőtlenségekre való gyakorlásra vagy módszerek megismerésére. (Manapság még a KöMaL A-ban néha szerepel ilyen, pl. A.571, de mint láttuk, azt is végig lehet tolni akár AM-GM-mel is :-). )
Ha már egyenlőtlenségeknél tartunk, mutatok sajátot is (szokásos jelölésekkel):
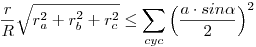 . .
Nem valami szép, sok minden bele van erőltetve, de azért van benne némi gondolkodás is.
Ezenkívül kitűznék egy nehezebb feladatot is, aki tud, mondjon megoldást.
|
| Előzmény: [3698] Fálesz Mihály, 2013-02-21 18:45:00 |
|
| [3698] Fálesz Mihály | 2013-02-21 18:45:00 |
 Bocs, a [3686]-ra akartam regálni, a [3688] elkerülte a figyelmemet.
A [3688]/a esetében valóban az a legegyszerűbb, ha új változókat vezetünk be, és ettől kezdve nincs háromszög, csak nemnegatív számok. (Btw, lehet egy lépéssel rövidebben, nincs szükség az xyz-vel való osztásra.)
A [3688]/b a (Neuberg-)Pedoe egyenlőtlenség egy változata, ami a KöMaL-ban is szerepelt (A. 468.). Ha két háromszög oldalai a,b,c, illetve A,B,C, a területük t, illetve T, akkor
a2(B2+C2-A2)+b2(C2+A2-B2)+c2(A2+B2-C2) 16tT. 16tT.
Egyenlőség akkor van, ha a két háromszög hasonló.
Abban a háromszögben, aminek az oldalai 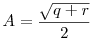 , , 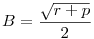 és és 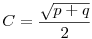 , azaz B2+C2-A2=p, C2+A2-B2=q és A2+B2-C2=r, a terület éppen , azaz B2+C2-A2=p, C2+A2-B2=q és A2+B2-C2=r, a terület éppen 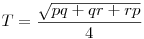 . .
(Mivel nem csak triviális esetekben van egyenlőség, ez elég nehézzé teszi a feladatot.)
* * *
Az érdekesség kérdéséről annyit, hogy sokezer háromváltozós szimmetrikus vagy ciklikus egyenlőtlenséget lehet találni az interneten, és ezeknek lényegében semmi üzenete vagy értelme nincsen. Egy időben voltak ilyenek az olimpián is, de miután egy csomó diák ráállt arra, hogy ilyeneket gyakoroljon tömegével, a háromváltozós egyenlőtlenségek háttérbe szorultak.
|
| Előzmény: [3691] w, 2013-02-21 15:26:54 |
|
| [3691] w | 2013-02-21 15:26:54 |
 "Hát, alaposan túlbonyolítottátok." - Ízlés kérdése, pl. szerintem a módszerem hasznosabb (a tiéd valóban szebb megoldás). Ezt mutatja, hogy a Te becslésed csak az eredeti egyenlőtlenségre jó (illetve egy csekély általánosításra), az (a) állításnál nem válik be.
"Csak tudnám, hogy ez az egyenlőtlenség miért "érdekes"..." - Az egyenlőtlenség (és főként az eredeti feladat) nem érdekes, ami érdekes, az az, hogy legalább 10-féle bizonyítása és 3-féle általánosítása van. A megoldási módszerek az érdekesek és tanulságosak.
Amúgy pedig a (b) változatra is gondolkodás nélkül alkalmazhatnánk az új változók bevezetését, csak bonyolult lenne.
|
| Előzmény: [3690] Fálesz Mihály, 2013-02-20 18:56:28 |
|
| [3690] Fálesz Mihály | 2013-02-20 18:56:28 |
 Hát, alaposan túlbonyolítottátok.
Jól ismert, hogy a terület és a (fél)kerület(négyzet) összehasonlításához az (s-a), (s-b) és (s-c) számok számtani és mértani közepeit érdemes venni:
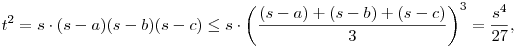
tehát 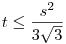 , egyenlőség csak s-a=s-b=s-c, vagyis szabályos háromszögre. , egyenlőség csak s-a=s-b=s-c, vagyis szabályos háromszögre.
Ha az oldalak négyzetösszege kell, akkor ezután jöhet a számtani-négyzetes az oldalakra.
(Csak tudnám, hogy ez az egyenlőtlenség miért "érdekes"...)
|
| Előzmény: [3689] w, 2013-02-20 10:54:27 |
|
| [3689] w | 2013-02-20 10:54:27 |
 Nem lövök le túl sokat, ha elmondom: az (a) részt a Róbert Gida által mondott módszerrel könnyebben meg lehet oldani, mint az eredetit, ujjgyakorlat. Átrendezve:
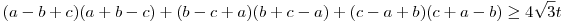 . .
Legyen x=-a+b+c, y=a-b+c, z=a+b-c, a Hérón-képlet miatt:
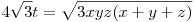 . Átírva az egyenlőtlenséget: . Átírva az egyenlőtlenséget:
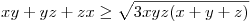
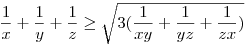
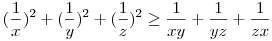 ismert, ekv. átalakítások miatt az eredeti is igaz. ismert, ekv. átalakítások miatt az eredeti is igaz.
|
| Előzmény: [3688] w, 2013-02-20 07:52:28 |
|
|
| [3687] Róbert Gida | 2013-02-19 21:46:12 |
 Nagyon ismerősnek tűnik. Gondolkodás nélkül: ha a,b,c egy háromszög oldalai, akkor a=y+z,b=x+z,c=x+y, ahol x=s-a,y=s-b,z=s-c és x,y,z>0 és ez visszafelé is igaz, ez nagyon hasznos az összes ilyen tipusú feladatnál, a háromszög kilőve. Héron képlettel: 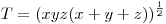 . Ezt beírva és négyzetre emelve a két oldalt és rendezve a bizonyítandó: . Ezt beírva és négyzetre emelve a két oldalt és rendezve a bizonyítandó: 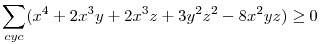 , ez pedig a számtani-mértani miatt igaz, az is látszik, hogy egyenlőség pontosan akkor van, ha x=y=z, azaz szabályos háromszögnél. , ez pedig a számtani-mértani miatt igaz, az is látszik, hogy egyenlőség pontosan akkor van, ha x=y=z, azaz szabályos háromszögnél.
|
| Előzmény: [3686] w, 2013-02-19 19:37:40 |
|
| [3686] w | 2013-02-19 19:37:40 |
 Adott egy háromszög, oldalai: a, b, c; területe t. Igazoljuk:
 . .
|
|
| [3685] jenei.attila | 2013-02-19 12:10:49 |
 Megnéztem a megoldást, szerintem a két konstrukció hasonló elvű, csak az enyém egyszerűbb. Egyébként először én is ezt a "hivatalos" megoldást adtam meg, és azután egyszerűsítettem.
|
| Előzmény: [3684] m2mm, 2013-02-19 00:26:45 |
|
| [3684] m2mm | 2013-02-19 00:26:45 |
 1 megoldásra emlékszem, az a hivatalos, megtalálható a 3681 hozzászólás linkjében. És igen, RMM a mostani hiv. név, régen volt ez RMMS, nekünk RMMC(C for competition) néven volt ismert.
|
| Előzmény: [3683] jenei.attila, 2013-02-16 08:42:56 |
|





 a4+b4+c4
a4+b4+c4 


 16tT.
16tT.