| [1336] vogel | 2010-09-19 21:27:52 |
 Először vizsgáld meg 1 kútra, 2 kútra... 2 kút esetén el lehet indulni egy kútból úgy, hogy tovább mehess egy másik kúthoz? Stb. Ha semmiképp sem megy, inkább konzultálj/gondolkodj a társaiddal az fmx (:-P) házikról, mert mindenre nem fogsz itt választ kapni.
|
| Előzmény: [1335] Fannka, 2010-09-19 21:06:18 |
|
| [1335] Fannka | 2010-09-19 21:06:18 |
 Egy kör alakú autópálya mentén benzinkutak vannak, bennük különböző mennyiségű benzin. Tudjuk, hogy összesen pont annyi benzin van szétosztva a kutak közt, amennyi egy kör megtételére elég. Bizonyítsuk be, hogy van olyan pontja a pályának, ahonnan egy autó üres tankkal elindulva végig tud menni a kutakban található benzin segítségével.
|
 |
|
|
| [1333] Fannka | 2010-09-19 20:43:13 |
 J És B felváltva írnak a tizedesvessző után számjegyeket végtelen sokáig. J nyer, ha a kapott szám racionális, B ha irracionális. Kinek van nyerő stratégiája? (ui: és köszi az előző megoldásokat:)
|
 |
|
|
| [1331] tamas553 | 2010-09-19 12:14:42 |
 Van két kitérő egyenesünk a térben:
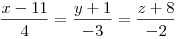

Mekkora a két egyenes távolsága?
|
|
| [1330] Kristóf Miklós 2 | 2010-09-18 16:33:47 |
 Kedves Jonas, köszönöm kedves válaszod, végre láttam egy egyszerűbb megoldást. Nekem ennél bonyolultabb jött ki. Bizonyára azért olyan népszerű, mert egyszerűen megfogalmazható, mégse egyszerű a megoldás.
|
| Előzmény: [1329] jonas, 2010-09-17 11:26:31 |
|
|
| [1328] Kristóf Miklós 2 | 2010-09-17 09:51:37 |
 Kedves Mindenki! Van egy aranyos feladatom, amit szeretnék megosztani veletek.
Van egy r sugarú legelő, és az egyik széléhez ki van kötve egy kecske. A kötél hossza R. A kecske mindent lelegel, amit elér. Milyen hosszú a kötél, ha a kecske a legelőnek épp a felét legeli le?
Adjuk meg 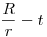 10 jegy pontosan! 10 jegy pontosan!
|
|
| [1327] jonas | 2010-09-16 17:09:58 |
 Én meg tudom csinálni n+1 lakattal is, bármi legyen is a k.
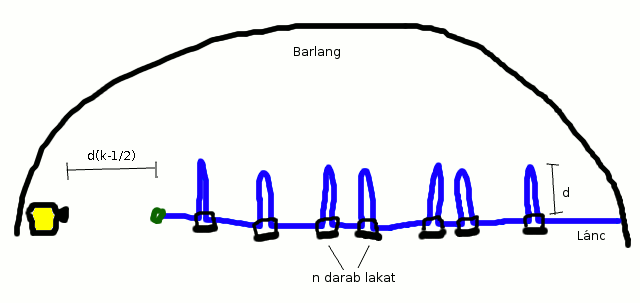
Rögzítsük a barlang egyik oldalához a kincsesládát, ezen legyen egy lakat. A lakat kulcsát rögzítsük egy hosszú láncra a barlang másik végéhez. A láncot n darab lakattal rövidebbre vesszük úgy, hogy minden rablóhoz pontosan egy lakatja van, és ehhez csak neki van kulcsa. Minden lakat két, egymástól d távolságra lévő láncszembe van beakasztva, és a lefogott d hosszú darabok nem fedik át egymást. A lánc hossza úgy van beállítva, hogy ha k lakatot kinyitnak, akkor már a végén lévő kulcs eléri a kincsesláda lakatját, de ha csak k-1-et nyitnak ki, akkor nem.
|
 |
| Előzmény: [1326] Róbert Gida, 2010-09-16 15:54:30 |
|
| [1326] Róbert Gida | 2010-09-16 15:54:30 |
 Még ennél is van jobb, ha nem egy szimplán leüthető lakatról van szó, hanem egy elektronikusról. Legyen N egy nagy pozitiv egész szám, a kulcs ami a széfet nyitja pedig egy random [N/2,N) intervallumba eső R egész. Az i-edik alkalmazott kulcsa az Rmod pi szám, ahol 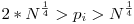 és pi prím (különbözőek). Bármely 4 összeáll, akkor ki tudják nyitni a zárat a kínai maradéktétel miatt (az elektronikus zár kiszámolja R-et a kínaiból), de bármely 3 még nem. és pi prím (különbözőek). Bármely 4 összeáll, akkor ki tudják nyitni a zárat a kínai maradéktétel miatt (az elektronikus zár kiszámolja R-et a kínaiból), de bármely 3 még nem.
|
| Előzmény: [1325] jonas, 2010-09-16 13:30:35 |
|
| [1325] jonas | 2010-09-16 13:30:35 |
 Az a feladat ide csak alsó becslést ad. A felső becslése csak arra az esetre vonatkozik, amikor minden zár közvetlenül az egy páncélszekrény ajtaján van.
Bizonyos n,k értékekre jobb konstrukciót lehet adni, ha használhatsz plusz ládákat. (Lehet, hogy az is segíthet, ha csak egy ládád van, de sorba köthetsz lakatokat esetleg láncot is használva, nem tudom.)
Mondok egy példa konstrukciót. Minden (t,v) számpárhoz, ahol 0 t t w w n egészek, vegyünk fel egy L(t,w) ládát, amibe majd néhány kulcsot rejtünk. Azt szeretnénk, hogy L(t,w)-t pontosan akkor lehessen kinyitni, ha együttműködik az R(0),R(1),...,R(w-1) rablók közül legalább t fő, meg még az R(w) rabló. Ezt az általános esetben úgy érjük el, hogy az L(t,w) ládán két lakat van, az elsőhöz csak az R(w) rablónak van kulcsa, a másikhoz viszont az L(t-1,t-1),L(t-1,t),...,L(t-1,w-1) ládák mindegyikébe rakunk egy kulcsot. Speciálisan azonban ha 0=t, akkor csak az első lakat legyen a ládán. Végük a kincset rakjuk egy külön ládába, és az ezen lévő egy lakathoz az L(k-1,k-1),L(k-1,k),...,L(k-1,n) ládába rejtsük. n egészek, vegyünk fel egy L(t,w) ládát, amibe majd néhány kulcsot rejtünk. Azt szeretnénk, hogy L(t,w)-t pontosan akkor lehessen kinyitni, ha együttműködik az R(0),R(1),...,R(w-1) rablók közül legalább t fő, meg még az R(w) rabló. Ezt az általános esetben úgy érjük el, hogy az L(t,w) ládán két lakat van, az elsőhöz csak az R(w) rablónak van kulcsa, a másikhoz viszont az L(t-1,t-1),L(t-1,t),...,L(t-1,w-1) ládák mindegyikébe rakunk egy kulcsot. Speciálisan azonban ha 0=t, akkor csak az első lakat legyen a ládán. Végük a kincset rakjuk egy külön ládába, és az ezen lévő egy lakathoz az L(k-1,k-1),L(k-1,k),...,L(k-1,n) ládába rejtsük.
Ezzel a megoldással elég összesen O(n2) láda, O(n2) lakat és O(n3) kulcs. Ez megfelelő n,k esetén olcsóbb lehet, mint a megoldásban leírt 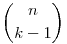 lakat. lakat.
(Arra vigyázni kell, hogy a ládák elég nehezek legyenek ahhoz, hogy ne lehessen ellopni őket. Vegyük viszont észre, hogy a megadott séma robosztus abban az értelemben, hogy k-nál kevesebb rabló nem tudja kulcsok ellopásával megakadályozni azt, hogy rablóknak másik, az előbbitől diszjunkt halmaza kinyithassa a ládát, így a kulcsokat nem szükséges a ládák belsejéhez láncolni.)
|
| Előzmény: [1324] Maga Péter, 2010-09-16 10:10:38 |
|
|
| [1323] Fannka | 2010-09-15 22:35:24 |
 ez matek: Van 10 rabló, akik egy végtelen sok lakattal lezárható kincsesládát akarnak lelakatolni úgy, hogy semelyik 3 ne tudja kinyitni, de bármely 4 igen. Legalább hány lakat kell ehhez, ha egy rabló több kulcsot is kaphat? Légyszi segítsetek!!!
|
 |
|
| [1322] Janosov Milán | 2010-09-14 18:01:04 |
 üdv, az elektronikus munkafüzetbe nem tudok bejelentkezni - azért, mert tavaly végeztem? ez esetben, a régebben texben beküldött megoldásaimat sem tudom már megnézni (törölve lettek)?
|
|
| [1321] SmallPotato | 2010-09-13 17:34:18 |
 A "súrlódási energia" számomra nem tűnik igazán kezelhető fogalomnak.
Ha jól értem, a gond ott van, hogy igazából a kerületi erő állandóságára lenne szükség, ami - a csökkenő sugár miatt - csökkenő fékezőnyomatékot igényelne. Ezt képletszerűen elég macerás lenne felírni, bár időben egyenletes sugárcsökkenéssel tán nem lőnénk nagyon mellé. A fő gond inkább az, hogy hogyan állítasz elő időben változó fékezőnyomatékot.
A pneumatikus féked tápnyomását kellene (tudni) változtatni a huzalerő függvényében. Amennyire tudom, ezt nagyban úgy oldják meg, hogy a huzal egy görgőn van eltérítve, a görgő pedig egy nyomásszabályzó szelep karjának végén van (vagyis épp a huzalerő szabályozza a tápnyomást).
|
| Előzmény: [1320] Abi8211, 2010-09-13 11:33:47 |
|
| [1320] Abi8211 | 2010-09-13 11:33:47 |
 Sziasztok!
Egy első ránézésre nagyon egyszerű kis problémával találom magam szemben. Van 1 forgó dobom, amiről folyamatosan tekercselem le a rá feltekercselt huzalt, megközelítőleg állandó sebességgel. Mivel a folyamatos letekercselés során csökken az átmérője a dobnak, és a tömege is, így a tehetetlenségi energiája folyamatosan csökken. A kérdésem az, hogy hogyan tudnám ezt legideálisabban fékezni, hogyan tudom meghatározni a súrlódási energiát ennek a rendszernek. Most jelenleg levegő működtetésű tárcsafék fékezi a rendszert, állandó nyomással, de letekercselés végén megnyújtja a huzalt, a túlzott fékhatás miatt szerintem. Segítségeteket előre is köszönöm! üdv:Robi
|
|
|
| [1318] bily71 | 2010-09-12 19:36:38 |
 Nézzük a jobboldalt tagonként:
a5=a1q4
a6=a1q5=a2q4
a7=a1q6=a2q5=a3q4
(itt azt használtuk fel, hogy an=amqn-m )
behelyettesítés után:
a5+a6+a7=a1q4+a2q4+a3q4
ebből a q4 tényezőt kiemelve kapjuk, hogy:
a5+a6+a7=q4(a1+a2+a3)
és innen már tudni fogod.
|
| Előzmény: [1317] gerpet, 2010-09-12 19:05:19 |
|
| [1317] gerpet | 2010-09-12 19:05:19 |
 Sziasztok! Lenne egy feladat, aminek a megoldását nem értem. Előre is elnézést kérek a rutinosabbaktól, hogy ilyen "egyszerű" (a feladatgyűjteményben, mint könnyű feladat szerepel) feladattal zargatlak benneteket. A feladat: "Egy mértani sorozat első hét tagjából az első három elem összege 26, a három utolsó elem összege pedig 2106. Mennyi a hét tag összege?" Az lenne a kérdésem, hogy az alábbi megoldásban az első egyenlőség hogyan jön ki?:
|
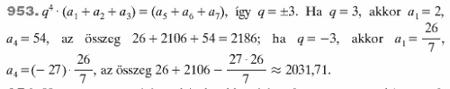 |
|
|
|
|
|
|









 t
t