|
|
|
|
| [1396] vogel | 2010-10-06 18:03:02 |
 Ez a sor miért divergens? 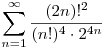 . Nem sikerült sehogy sem alulról becsülnöm. Biztos könnyű. Köszönöm. . Nem sikerült sehogy sem alulról becsülnöm. Biztos könnyű. Köszönöm.
|
|
| [1395] David820607 | 2010-10-06 16:46:06 |
 Létezik (nem csupa azonos tagból álló) tetszőlegesen hosszú számtani sorozat csupa teljes hatványból?
|
|
| [1394] Szekér István | 2010-10-06 15:44:39 |
 Helló, ez most nem matekos kérdés lesz:
Amikor regisztráltam, majd beléptem, ezt kérdezte: hanyadik osztályba jársz 2009/2010 tanévben (ami a tavalyi tanév volt) kiválasztom, hogy 9. osztály (most 10.-es vagyok), aztán jöttem rá, hogy ez nem jeó. Hogy tudom megváltoztatni az évfolyamom? Regisztráljak újra?
|
|
|
| [1392] Khesteg | 2010-10-02 22:09:22 |
 Eh...tényleg. Nem vettem észre hogy lehet egyszerűsíteni. Köszi szépen a segítséget :)
|
|
|
| [1390] Khesteg | 2010-10-02 18:27:18 |
 Hát ebből nekem nem jön ki mert a határérték végig 0/0 alakú marad, mert nem tűnik el a nevezőből az x.
|
|
|
| [1388] Khesteg | 2010-10-02 17:11:55 |
 Valaki le tudná nekem vezetni a lim(x tart 0-hoz) x(az x-ediken) megoldását plz? Nem igazán tudom összehozni olyan alakra hogy alkalmazhassam a L'Hospital szabályt...vagy az nem is kell?
|
|
| [1387] Maga Péter | 2010-09-23 11:33:26 |
 Nem egészen. A wikipedia azt mondja, hogy  (2)-ről Euler 1735-ben mutatta meg, hogy (2)-ről Euler 1735-ben mutatta meg, hogy 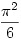 , de a , de a  2-ről csak 1794-ben bizonyította be Legendre, hogy irracionális. Euler pedig 1783-ban meghalt. 2-ről csak 1794-ben bizonyította be Legendre, hogy irracionális. Euler pedig 1783-ban meghalt.
Valójában Euler bizonyítása (arra, hogy végtelen sok prím van) úgy nézett ki, hogy a
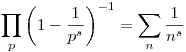
s>1 feltétel mellett fennálló azonosságban tartott s-sel 1-hez. Ha pedig indirekte véges sok prím lenne, akkor a szorzat egy véges számhoz, az összeg pedig a végtelenbe tartana.
|
| Előzmény: [1386] bily71, 2010-09-23 09:27:08 |
|
|
|
|
| [1383] Maga Péter | 2010-09-22 22:23:31 |
 Azt mondod [1372]-ben, hogy ,,Én nem azt mondom, hogy közelebb kerülnénk a Brun-konstans problémájának megoldásához (...)''
Vesd már ezt össze a [1367]-es hozzászólásoddal: ,,"Az ikerprímsejtés bebizonyításával semmivel nem jutsz közelebb Brunhoz..."'' (ezt RG [1366]-osából idézed)
,,De igen!''
Most akkor mi van???
|
| Előzmény: [1372] bily71, 2010-09-21 17:21:48 |
|
|
|
|
|
|
| [1377] bily71 | 2010-09-22 12:38:37 |
 Tehát mégegyszer:
(i) a fában ugyanannyi elágazás (csúcs) van, mint valós szám,
(ii) a szintek száma megszámlálhatóan végtelen,
(iii) minden szinten véges sok elágazás van, (az n-edik szinten 10n darab),
(iv) alkossanak az egy szinten lévő elágazások halmazokat,
(v) megszámlálhatóan végtelen sok véges elemszámú halmaz uniója megszámlálhatóan végtelen sok elemü halmazt eredményez.
Hol a hiba?
|
| Előzmény: [1373] bily71, 2010-09-21 17:47:53 |
|
|






 esetén
esetén 
 (2)-ről Euler 1735-ben mutatta meg, hogy
(2)-ről Euler 1735-ben mutatta meg, hogy  2-ről csak 1794-ben bizonyította be Legendre, hogy irracionális. Euler pedig 1783-ban meghalt.
2-ről csak 1794-ben bizonyította be Legendre, hogy irracionális. Euler pedig 1783-ban meghalt. 
