| [1453] Fálesz Mihály | 2011-01-25 17:31:12 |
 (Komplex) sajátértékből mindig annyi van, mint a mátrix mérete.
A különböző sajátértékekhez tartozó sajátvektorok mindig lineárisan függetlenek, de ha vannak többszörös sajátértékek, akkor lehetséges, hogy kevesebb független sajátvektor van, mint a mátrix mérete.
A 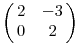 mátrix karakterisztikus polinomja az (x-2)2, tehát a 2 kétszeres sajátérték. A sajátvektorok az mátrix karakterisztikus polinomja az (x-2)2, tehát a 2 kétszeres sajátérték. A sajátvektorok az 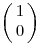 többszörösei, a (2 sajátértékhez tartozó) sajátaltér csak egydimenziós. többszörösei, a (2 sajátértékhez tartozó) sajátaltér csak egydimenziós.
|
| Előzmény: [1452] ga.bakonyi, 2011-01-25 17:04:25 |
|
| [1452] ga.bakonyi | 2011-01-25 17:04:25 |
 Szép napot mindenkinek!
Azt szeretném kérdezni, hogy elképzelhető-e, hogy 2x2-es kvadratikus mátrixnak egyetlen sajátértéke van?
A következő feladattal kapcsolatban merült fel a probléma:
Határozza meg A mátrix inverzének sajátértékeit!
a11=2 ; a12=-3 ; a21=0 a22=2
Erre invertálás után, a sajátértékegyenletből azt kaptam, hogy A inverzének egy sajátértéke van, és az 1/2.
Olyan másodfokú egyenletetet persze már láttam, aminek csak egy gyöke van, de olyan kvadratikus mátrixot még nem, aminek csak egy sajátértéke. Ezért gyanús, hogy elrontottam valamit, vagy az invertálásnál vagy a sajátérték meghatározásánál.
Köszönöm a segítséget!
|
|
|
| [1450] Maga Péter | 2011-01-20 11:37:49 |
 Ennél egyszerűbbet?:)
Kicsivel kevesebbet kell számolni, ha először végzed el a parciális törtekre bontást (egész együtthatósak a faktorok), és utána a polinomosztást, mint ha fordított sorrendben csinálod. Én legalábbis gyorsabban osztok első-, mint másodfokú polinommal.
|
| Előzmény: [1449] Hölder, 2011-01-20 10:23:08 |
|
| [1449] Hölder | 2011-01-20 10:23:08 |
 Sziasztok! Ti hogyan integrálnátk a következő fv-t? x10/(x2+x-2) Azaz x 10 hatványon és x a 2 hatványon van. Én polinomosztással, de lehet, hogy van egyszerűbb is, erre volnék kiváncsi.
|
|
| [1448] Valvehead | 2011-01-13 13:11:58 |
 hm.. szerintem nem lehet megúszni differenciál egyenlet nélkül, mert a kezdősebesség végtelen nagy (azaz az induló sebessége a bolytól). v pillanatnyi*s=állandó=0.02[m négyzet/sec] (ds/dt)*s(t)=0.02 Ezt kell megoldani és s(t1)=2-ből kifejezni a megoldást.
|
| Előzmény: [1447] csyabi, 2011-01-13 08:21:38 |
|
| [1447] csyabi | 2011-01-13 08:21:38 |
 Kedves Segítőkész Fórumozók!
Az alábbi feladathoz szeretnék megoldási ötleteket kérni:
"Egy hangya a bolytól egyenes vonal mentén távolodik, úgy, hogy sebessége fordítottan arányos a bolytól mért távolságával. Amikor a hangya a bolytól 1 m-re van, sebessége 2 cm/s. Mennyi idő múlva ér a hangya 2 m távolságra a bolytól?"
A válaszokat előre is köszönöm!
|
|
| [1446] R.R King | 2011-01-03 18:23:25 |
 Az egyik matematikai folyóiratban van kitűzve egy feladat, ami erre az összegzésre vezet. Biz be, hogy 2n-1 pontosan akkor osztója n!-nak, ha n kettőhatvány és n pozitív egész.
|
| Előzmény: [1445] epsilon, 2011-01-03 17:52:28 |
|
|
|
| [1443] epsilon | 2011-01-03 16:40:00 |
 Üdv Mindenkinek, és BÚÉK! Lenne egy kérdésem: Melyek azok a pozitív egész m értékek, amelyekre teljesül az alábbi egyenlőség? ([a] az a valós szám egész része). Ahogy sejtem, az m muszáj 2-nek egy hatványa legyen (akár nulladik is), de nem tudom bizonyítani. Valaki tudna-e segíteni? Előre is köszönöm, üdv: epsilon
|
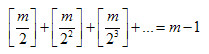 |
|
| [1442] SmallPotato | 2010-12-28 17:03:21 |
 Az előbbi hozzászólás magyar fordítása:
Legközelebb légy szíves körülnézni, nincs-e már olyan futó topik, amelybe a problémád illik, és
- ha van (és itt most bizony lett volna, nem is egy), akkor abban tedd közzé a gondodat,
- ha pedig netán nincs, akkor olyan új topikot nyiss, amelynek címéből minél konkrétabban kiderül annak célja, tartalma.
|
| Előzmény: [1439] LK, 2010-12-28 14:01:54 |
|
| [1441] Róbert Gida | 2010-12-28 16:11:22 |
 Az ilyen topikokat gondolkodás nélkül törtlik jobb helyeken. Már csak a cím választása miatt.
|
|
|
| [1439] LK | 2010-12-28 14:01:54 |
 sinx-ctgx=0 Oldja meg valós számok halmazán!
|
|
| [1437] R.R King | 2010-12-04 13:12:08 |
 Talán teljes függvényvizsgálatot kellett végezni. Emelt szinten csinálnak ilyeneket. Bár nem tudom, de ha nem specmatos osztályról van szó, akkor a fenti témában pl. simán el tudom képzelni.
|
| Előzmény: [1436] HoA, 2010-12-04 13:04:24 |
|
| [1436] HoA | 2010-12-04 13:04:24 |
 Kár, hogy leszedtétek innen az arcát kezébe temető ember képét. Szerintem is elgondolkodtató a feladat, kedves matematika-kedvelők és -oktatók. Nem annyira matematikai, mimt okatatás-pszihológiai és valószínűségszámítási. Feltételezett ismeret a középiskolai matemetika tematika. Fel is adom:
Mi a legvalószínűbb, mi lehetett annak a feladata, aki annyit tud róla, hogy a feladat az f(x)=e-1/x függvény ?
|
| Előzmény: [1429] Sirpi, 2010-12-02 14:41:49 |
|
|
|
|
|
|
| [1427] PAL | 2010-11-03 00:12:19 |
 Én igen. Pont van itthon egy olyanom, méghozzá a perpetuator nevű csoda is megvan hozzá, bár azt épp szervizelni kéne...
Film róla itt: http://www.youtube.com/watch?v=YOQyn6c1Kc4
(alatta érdemes elolvasni a hozzászólásokat, az enyim pl. a /a Lenz-törvényes megközelítés, nna7yk-tól / sajnos hamar rámutatott fizikai ismereteim hiányosságára...
Egyébként, ha érdekel téged (vagy bárki mást!), és megoldható, én szívesen megmutatom az eszközt. Itt akár meg is szervezhetünk egy találkozót, ahol láthatod működés közben, merthát szerintem roppant érdekes élőben látni a szerkentyűt /én Budapest XVI. kerületéhez közel lakom / Nem véletlenül láttam például valami ehhez hasonlót kiállítva anno a Csodák Palotájában is, bár annak már vagy jó 10 éve...
Régebben többet foglalkoztam ezzel, bár addig nem jutottam el, hogy fizikus szemmel nézve megértsem a működését, mivel csupán a főiskolai matematika eszköztára és a középiskola fizika ismeretanyaga állt rendelkezésemre és azzal sajnos nem jutottam sokra a Levitron fizikájával szemben.
Pedig például nagyon érdekelt volna (sőt egy kicsit ma is érdekel), hogy 1) mit 2) és miért, azt mutatja a precíziós mérleg, amit akkor láttam, amikor rátettem és megmértem a lebegő pörgettyűvel együtt a mágnes tömegét…? (a poént nem lövöm le, de sejthető persze, hogy a Newton-törvények ilyenkor is nyilván érvényesek, vagyis a pörgettyű közvetve nyomja az alátámasztást, csakhát ez a "közvetve" ebben az esetben némi fizikai magyarázatra szorul... ) 3)... nem világos számomra ugyanis, hogy ilyenkor hogyan kell értelmezni a test súlyát és tömegét? (úgy értem hogyan kell például egy tankönyvekben is látható sematikus ábrába berajzolni a lebegő test által a mérlegre közvetve ható G súlyerőt (vagyis az azt szimbolizáló erővektor támadáspontját), úgy hogy, ha teszem azt, még egy vizes edényt is a két mágnes, tehát a mágnesgyűrű és a lebegő levitron közé helyezek (ezt ugyanis a gyakorlatban megtettem méréskor)
Esetleg egy ilyen számítást, mint feladat megnéznék, akár itt a fórumon is... A cél tehát legyen az előbbi feladat megoldása, középiskolai fizika ismereteket felhasználva teljesértékű (=ábra+számítás+magyarázat) választ adni arra, hogy:
Mit mutat a mérleg, ha ráhelyezzük a mágnes-talpat, majd fölötte egy poharat tartunk mondjuk a kezünkben, amelyben víz van, és a lebegő pörgettyű ezen víz felett lebeg, benne a pohárban (természetesen nincs érintkezés a pörgettyű és a víz között ) ? A szükséges kiinduló számadatok ismeretlenek, (feltételezhető hogy adott m(lev),H(neodínium-mágnes), stb.) mindezek megtalálhatók az angol nyelvű dokumentumokban (kicsit lentebb) vagy igény esetén én is megmérhetem a meglévő eszközeim paramétereit.
(sajnos tudom, ez így kicsit pongyola megfogalmazása volt egy fizika-feladatnak, de ez az álatalam végzett kísérlet vázlatos leírása, fizikában járatosak nézzék el ezt nekem)
Tehát, akit érdekel az eszköz elméleti fizikába illesztett részletes vizsgálata tanulmány formájában, akkor katt ide:
1. változat http://www.physics.ucla.edu/marty/levitron/spinstab.pdf
2. változat http://physik.uibk.ac.at/hephy/maturanten/levitron/Jones/jones.pdf
(magyar szakfordítást nem találtam, így fizikához minimum fősikolai, de inkább egyetemi szinten értő lelkes amatőrök esetleg elkészíthetik valamelyiknek a tükörfordítását is, csak hogy olyanunk is legyen!)
|
| Előzmény: [1426] futlac, 2010-11-02 17:51:34 |
|
| [1426] futlac | 2010-11-02 17:51:34 |
 Valaki meg tudná nekem élőben mutatni a mágneses pörgettyűt amint a másik mágnes fölött lebeg?(Levitron.) Előre is köszönöm: futlac
|
|
| [1425] epsilon | 2010-11-01 11:14:52 |
 Jó, akkor részletezem: Az f(x)-et válasszuk szét így: f(x)=p+x.g(x), tehát f(p)=p(1+g(p))=p.r Az r=1 azt jelentené, hogy g(p)=0, de akkor sorra számolnánk f(p.p), f(p.p.p)...értékeket, ezek is ugyanoda vezetnek, és valamelyik esetben az r csak nem lesz 1 mert ellenkező esetben a g polinomnak végtelen sok gyöke lesz, a p, p.p, p.p.p,....alakú számok közül. Gondolom, így már jó.
|
| Előzmény: [1424] Sirpi, 2010-11-01 10:42:55 |
|






 m<2n+1. Ekkor a bal oldalon az utolsó nem 0 tag az
m<2n+1. Ekkor a bal oldalon az utolsó nem 0 tag az