| [1467] lorantfy | 2011-01-29 14:11:45 |
 Az akinek van olyan gépe, amivel numerikusan ki tudja integrálni, akár ki is dobhatja ezeket a táblázatokat, feltéve, hogy a gépe nem 3V-os gombbelemmel működik, ami ha esetleg lemerülne nem kapható a közelben lévő éjjel nappal nyitva tartó FICKO áruházban. Ilyenkor aztán lehetséges, hogy arra fog kényszerülni, hogy a szemétből előkeresse a kidobott táblázatokat, ha véletlenül nem környezetvédő és nem vitte el már korábban a legközelebbi szelektív hulladékgyűjtőbe. Ekkor persze letölthetné a Netről, de ha javaslatodnak megfelelően onnan is kidobták ezeket, akkor arra kényszerül, hogy elmenjen és kihalássza a szelektív gyűjtőből, azt remélve, hogy azóta nem ürítették ki a tartályt. Ha véletlenül kiürítették, akkor még mindig bízhat abban, hogy van a Földön olyan ember, aki csupán heccből betanulta az egész Fi(z) táblázatot. Gondolva arra, hogy a Föld mágneses terének csökkenésével egy esetleges nagyobb napkitörés az egész földi számítógépes rendszert tönkre teszi.
|
| Előzmény: [1466] Róbert Gida, 2011-01-29 12:28:26 |
|
|
| [1465] Jhony | 2011-01-29 12:23:34 |
 Bocsánat ! ... igen valóban ,... a kérdés pedig az lenne HOGY bizonyítjuk be , hogy ebben az esetben n bármely értékére létezik egy k és egy p ,,különböző" szám mire az egyenlet igaz !
|
| Előzmény: [1463] SmallPotato, 2011-01-29 11:24:24 |
|
|
| [1463] SmallPotato | 2011-01-29 11:24:24 |
 Nem, ez elméletileg sem igaz. Egy azonosság bizonyítása azt jelenti, hogy kimutatjuk: a felírt egyenlőség a benne szereplő változók bármely megengedett értéke mellett teljesül. A szóban forgó egyenlőség pl n=2, p=0 és k=0 esetben nem igaz, tehát van ellenpélda. Persze végtelen sok ellenpélda van ... de ha csak egyetlen is akad, akkor már nincs mit bizonyítani.
|
| Előzmény: [1461] Jhony, 2011-01-29 10:23:55 |
|
|
| [1461] Jhony | 2011-01-29 10:23:55 |
 Köszönöm ! ...,de így akadtam rá ! ... és elméletileg ez igaz is ,mert ,ha n=2,p=0,k=1 ebben az esetben az ,,állítás" igaz ... és így tovább. szóval csak egy bizonyítás levezetését lehet-e erre ,,csinálni" ??? KÖSZÖNÖM SZÉPEN !
|
| Előzmény: [1460] SmallPotato, 2011-01-29 01:35:14 |
|
|
| [1459] Jhony | 2011-01-28 23:46:00 |
 Tisztelt Fórumozók ! SEGÍTSETEK !!! KÖSZÖNÖM !
Ha n=2,3,4,5,...,+végtelenig, p=0,1,2,...,+végtelenig és k=0,1,2,...,+végtelenig akkor az n=k+p+1 bizonyítása mi lenne ?
|
|
| [1458] ga.bakonyi | 2011-01-26 22:40:28 |
 Fogalmam sincs, előttem volt a feladatlap, onnan másoltam szó szerint, és ott 144cm volt. (lehet, hogy csak sajthiba) De gyakorlatilag azt hiszem úgyis a variancia négyzetgyökével kell majd számolni... Csak nem áll össze a feladat koncepcionálisan a fejemben.
|
| Előzmény: [1457] jonas, 2011-01-26 21:49:05 |
|
|
| [1456] ga.bakonyi | 2011-01-26 21:35:05 |
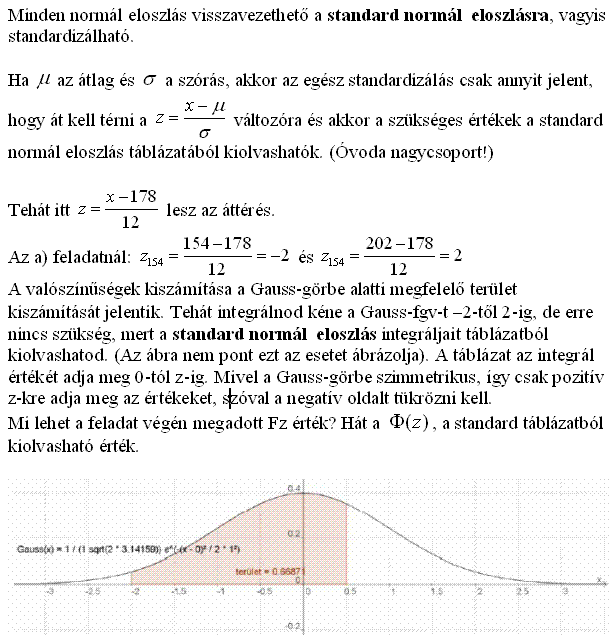
 Szép estét mindenkinek! Most egy szép normális eloszlásos feladatot hoztam a valószínűség-számítás témaköréből. Lövésem sincs, hogyan kell megoldani, ezért kérek segítséget. Íme:
"Egy felmérés során megállapították, hogy a vizsgált csoportban a férfiak magassága normális eloszlást követ. Az átlagos magasság 178 cm, a variancia 144 cm.
a) Mekkora a valószínűsége, hogy egy véletlenszerűen kiválasztott férfi magassága 154 cm és 202 cm közé esik?
b) Mekkora a valószínűsége, hogy három véletlenszerűen kiválasztott férfi közül mindhárom 166 cm-nél alacsonyabb?
c) Mekkora a valószínűsége, hogy egy véletlenszerűen kiválasztott férf testmagassága nagyobb lesz 178 cm-nél?
d) Milyen valószínűséggel lesz egy véletlenszerűen kiválasztott férfi testmagassága a várható értéknél kétszeres szórással kevesebb?
(Fz(2)=0,9772, Fz(1)=1, 8413 "
Hát, eddig a feladat. Elvileg holnapra kéne, de bármikor kíváncsi vagyok a megoldásra. Nagyon szépen köszönöm a segítséget.
|
|
| [1455] ga.bakonyi | 2011-01-25 20:35:42 |
 Köszönöm a gyors válaszokat! Csak annyi, hogy én ennek a mátrixnak az inverzének a sajátértékeire gondoltam (pontosabban a feladat "arra gondolt") de azt hiszem így is választ kaptam a kérdésemre. Még egyszer köszönöm.
|
|
|
| [1453] Fálesz Mihály | 2011-01-25 17:31:12 |
 (Komplex) sajátértékből mindig annyi van, mint a mátrix mérete.
A különböző sajátértékekhez tartozó sajátvektorok mindig lineárisan függetlenek, de ha vannak többszörös sajátértékek, akkor lehetséges, hogy kevesebb független sajátvektor van, mint a mátrix mérete.
A 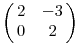 mátrix karakterisztikus polinomja az (x-2)2, tehát a 2 kétszeres sajátérték. A sajátvektorok az mátrix karakterisztikus polinomja az (x-2)2, tehát a 2 kétszeres sajátérték. A sajátvektorok az 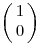 többszörösei, a (2 sajátértékhez tartozó) sajátaltér csak egydimenziós. többszörösei, a (2 sajátértékhez tartozó) sajátaltér csak egydimenziós.
|
| Előzmény: [1452] ga.bakonyi, 2011-01-25 17:04:25 |
|
| [1452] ga.bakonyi | 2011-01-25 17:04:25 |
 Szép napot mindenkinek!
Azt szeretném kérdezni, hogy elképzelhető-e, hogy 2x2-es kvadratikus mátrixnak egyetlen sajátértéke van?
A következő feladattal kapcsolatban merült fel a probléma:
Határozza meg A mátrix inverzének sajátértékeit!
a11=2 ; a12=-3 ; a21=0 a22=2
Erre invertálás után, a sajátértékegyenletből azt kaptam, hogy A inverzének egy sajátértéke van, és az 1/2.
Olyan másodfokú egyenletetet persze már láttam, aminek csak egy gyöke van, de olyan kvadratikus mátrixot még nem, aminek csak egy sajátértéke. Ezért gyanús, hogy elrontottam valamit, vagy az invertálásnál vagy a sajátérték meghatározásánál.
Köszönöm a segítséget!
|
|
|
| [1450] Maga Péter | 2011-01-20 11:37:49 |
 Ennél egyszerűbbet?:)
Kicsivel kevesebbet kell számolni, ha először végzed el a parciális törtekre bontást (egész együtthatósak a faktorok), és utána a polinomosztást, mint ha fordított sorrendben csinálod. Én legalábbis gyorsabban osztok első-, mint másodfokú polinommal.
|
| Előzmény: [1449] Hölder, 2011-01-20 10:23:08 |
|
| [1449] Hölder | 2011-01-20 10:23:08 |
 Sziasztok! Ti hogyan integrálnátk a következő fv-t? x10/(x2+x-2) Azaz x 10 hatványon és x a 2 hatványon van. Én polinomosztással, de lehet, hogy van egyszerűbb is, erre volnék kiváncsi.
|
|
| [1448] Valvehead | 2011-01-13 13:11:58 |
 hm.. szerintem nem lehet megúszni differenciál egyenlet nélkül, mert a kezdősebesség végtelen nagy (azaz az induló sebessége a bolytól). v pillanatnyi*s=állandó=0.02[m négyzet/sec] (ds/dt)*s(t)=0.02 Ezt kell megoldani és s(t1)=2-ből kifejezni a megoldást.
|
| Előzmény: [1447] csyabi, 2011-01-13 08:21:38 |
|
| [1447] csyabi | 2011-01-13 08:21:38 |
 Kedves Segítőkész Fórumozók!
Az alábbi feladathoz szeretnék megoldási ötleteket kérni:
"Egy hangya a bolytól egyenes vonal mentén távolodik, úgy, hogy sebessége fordítottan arányos a bolytól mért távolságával. Amikor a hangya a bolytól 1 m-re van, sebessége 2 cm/s. Mennyi idő múlva ér a hangya 2 m távolságra a bolytól?"
A válaszokat előre is köszönöm!
|
|
| [1446] R.R King | 2011-01-03 18:23:25 |
 Az egyik matematikai folyóiratban van kitűzve egy feladat, ami erre az összegzésre vezet. Biz be, hogy 2n-1 pontosan akkor osztója n!-nak, ha n kettőhatvány és n pozitív egész.
|
| Előzmény: [1445] epsilon, 2011-01-03 17:52:28 |
|
|
|
| [1443] epsilon | 2011-01-03 16:40:00 |
 Üdv Mindenkinek, és BÚÉK! Lenne egy kérdésem: Melyek azok a pozitív egész m értékek, amelyekre teljesül az alábbi egyenlőség? ([a] az a valós szám egész része). Ahogy sejtem, az m muszáj 2-nek egy hatványa legyen (akár nulladik is), de nem tudom bizonyítani. Valaki tudna-e segíteni? Előre is köszönöm, üdv: epsilon
|
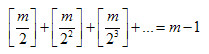 |
|











 m<2n+1. Ekkor a bal oldalon az utolsó nem 0 tag az
m<2n+1. Ekkor a bal oldalon az utolsó nem 0 tag az