| [1691] TLevi | 2012-03-14 13:30:41 |
 Sziasztok!...variacio egy temara:
Segitseget szeretnek egy egyenlet megoldasahoz! Az egyenletet mellekelem "*.jpg" formatumban. Nem tudom, hogyan kell kifejeznem a "lambdat" a tobbi ertek fuggvenyeben. (csak a lambda ismeretlen) Elore is koszonom a segitseget!
|
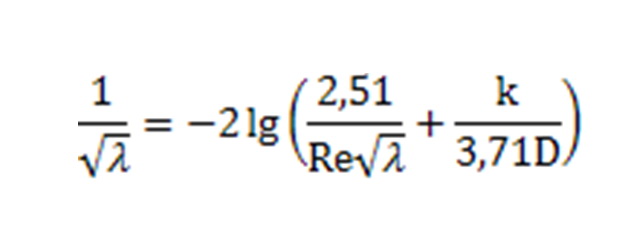 |
|
| [1690] TLevi | 2012-03-14 13:28:54 |
 Sziasztok!
Segitseget szeretnek egy egyenlet megoldasahoz! Az egyenletet mellekelem "*.jpg" formatumban. Nem tudom, hogyan kell kifejeznem a "lambdat" a tobbi ertek fuggvenyeben. (csak a lambda ismeretlen) Elore is koszonom a segitseget!
Udv, TLevi
|
 |
|
| [1689] Lóczi Lajos | 2012-03-14 09:31:59 |
 Először is pontosítanod kell a feladatot.
Pl. x a változó? Valós?
 egy paraméter? Valós? Pozitív? 1-nél nagyobb? egy paraméter? Valós? Pozitív? 1-nél nagyobb?
Az aszimptotikus egyenlőséget hol érted? Ha x  ? (Különben a függvény nem is invertálható mindenhol.) ? (Különben a függvény nem is invertálható mindenhol.)
Milyen tételre hivatkoznak?
Próbáld az aszimptotikus egyenlőség két oldalán szereplő kifejezések hányadosának limeszét vizsgálni úgy, hogy "új változót" vezetsz be és így az inverzfüggvény kiküszöbölhető.
|
| Előzmény: [1688] Zine, 2012-03-13 21:38:16 |
|
| [1688] Zine | 2012-03-13 21:38:16 |
 Nem szeretnék megoldást kapni, csak ötletet szeretnék kérni, hogyan lehetne belátni a következőt:
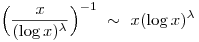
ahol a baloldal a -1-edik hatvány az inverzfüggvényt jelöli. Egy tétel felhasználásával ki tudom hozni, azonban magát a tételt nem teljesen értem, így ettől különböző megoldást szeretnék találni. Előre is köszönöm!
|
|
|
|
| [1685] Moderátor | 2012-03-06 15:43:09 |
 Jhony több hozzászólását és az ezekre érkezett válaszokat töröltem.
|
|
| [1677] jenei.attila | 2012-02-20 11:38:14 |
 Az "érdekes kérdést" tekintsétek semmisnek, mert butaság. Egybevágóságnak az alakzatot önmagába vivő egybevágósági transzformációt nevezünk, amik definíció szerint tükrözés forgatás, eltolás és csúsztatva tükrözés lehetnek. Korlátos alakzatra csak a tükrözés és a forgatás jön szóba, amiknek van fixpontjuk. Egy korlátos alakzatnak csak egy forgásszimmetria középpontja lehet (viszont több különböző szögű forgásszimmetriája lehet ugyanazon pont körül), és az összes szimmetria tengely ezen a ponton halad át (vagy csak egy tengelyes szimmetriája van). Ez igaz?
|
| Előzmény: [1676] jenei.attila, 2012-02-20 11:13:05 |
|
| [1676] jenei.attila | 2012-02-20 11:13:05 |
 Igazad lehet. Hirtelen ez jutott eszembe, de valóban egyszerűbb és talán általánosabb a csúsztatva tükrözésekkel operálni. A lényeg az, hogy a három nem egy ponton átmenő tengelyre való egymás utáni tükrözések által meghatározott csúsztatva tükrözést páros sokszor alkalmazva egy kiválasztott pontra, a kép pontok mindig egy adott (jó esetben nem nullvektorú) eltolással kerülnek arrébb. Ezek a pontok szintén az alakzat pontjai, ami ellentmond annak, hogy az alakzat korlátos. Szerintem ez lesz a jó megoldás. Most már viszont érdekes kérdés, hogy vajon van-e olyan (korlátos) alakzat, amelyre nem alkalmazható a Brouwer tétel, és létezik fixpont mentes egybevágósága. Vagy az egybevágóságnak mindig van fixpontja, ha az alakzat korlátos? A Brouwer tételhez talán nem kell a konvexitás, elég lehet a zárt körlemezzel való homeomorfia, vagy rosszul gondolom?
|
| Előzmény: [1675] Fálesz Mihály, 2012-02-20 09:45:52 |
|
| [1675] Fálesz Mihály | 2012-02-20 09:45:52 |
 Szia Attila,
Egy egybevágóság fixpontjainak keresésére a Brouwer-tételt kicsit nagy ágyúnak éreztem, ezért kotyogtam bele. (Közben elolvastam alaposabban, amit írtál. :-) )
Ha a Brouwer-tétellel akarjuk az állítást lebombázni, akkor ki kell találnunk egy konvex (esetleg csak a körlemezzel homeomorf), kompakt, és nem üres halmazt, amit az illető egybevágóság önmagába képez. Ez a halmaz lehet például az L konvex burkának lezártja, mert ez az operáció felcserélhető az egybevágóságokkal.
A csúsztatva tükrözést én kétszer hajtanám végre, hogy egy sima eltolás legyen belőle. (Bármelyik megoldásról is legyen szó, meg kell dolgozni azért, hogy véletlenül ne a nullvektorral toljunk el.)
Üdv.
F.M.
|
| Előzmény: [1673] jenei.attila, 2012-02-20 09:03:20 |
|
| [1673] jenei.attila | 2012-02-20 09:03:20 |
 Lehet, hogy igazad van, és nem kell bevetni a fixpontokat. Három nem egy ponton átmenő egyenesre történő egymás utáni tükrözés egy csúsztatva tükrözés. Ha kiválasztjuk az alakzat egy pontját és erre alkalmazzuk többször a csúsztatva tükrözést (az eredmény szintén az alakzat pontja kell hogy legyen), akkor az eredetitől egyre távolodó pontokat kapunk, ami ellentmond annak, hogy az alakzat korlátos. Elképzelhető, hogy létezik olyan korlátos alakzat (pl. nyílt körlemez?)amelyre nem alkalmazható a Brouwer tétel (persze ettől még lehetséges, hogy bármely egybevágóságának van fixpontja), viszont igaz rá az eredeti állítás.
|
| Előzmény: [1674] Fálesz Mihály, 2012-02-19 14:04:27 |
|
| [1672] jenei.attila | 2012-02-19 23:08:24 |
 Azt hiszem félre értetted, vagy én nem fogalmaztam elég világosan. Én azt írtam, hogy az alfa szögű forgásszimmetriából csak akkor következik a középpontos szimmetria, ha igaz az a feltétel amit írtam. Tehát ha csak annyit tudunk, hogy az alakzatnak van egy alfa szögű forgásszimmetriája, abból csak a mondott feltétel mellet következik a középpontos szimmetria. Te fordítva értelmezted: abból, hogy az alakzat középpontosan szimmetrikus, nyilván nem következik hogy csak a feltételnek megfelelő egyéb alfa szögű forgásszimetriája van csak (vagy ami ugyanez: ha létezik a feltételnek nem megfelelő forgásszimmetria akkor nem igaz az, hogy nem lehet középpontosan szimmetrikus), és ezt nem is állítottam. A körlap nyilván középpontosan szimmetrikus, de nem is csak a feltételnek megfelelő egyéb forgásszimmetriája van. Továbbra is fenntartom, hogy pl. a 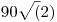 fok forgásszimmetriából nem következik a középpontos szimmetria, de létezik olyan alakzat, aminek mindkét szimmetriája megvan (pl. a körlap). Remélem így már érthető. fok forgásszimmetriából nem következik a középpontos szimmetria, de létezik olyan alakzat, aminek mindkét szimmetriája megvan (pl. a körlap). Remélem így már érthető.
|
| Előzmény: [1671] Róbert Gida, 2012-02-19 22:17:31 |
|
|
| [1670] jenei.attila | 2012-02-19 17:49:47 |
 A 2. kérdésedre válaszolva: Egyik sem igaz. Ha pl. egy nem egyenlő szárú háromszöget a legkisebb szögű csúcsa körül 120, illetve 240 fokkal elforgatunk, akkor egy olyan alakzatot kapunk ami se középpontosan, se tengelyesen nem szimmetrikus. Középpontosan akkor lenne szimmetrikus egy alfa szögű elforgatásra nézve szimmetrikus alakzat (feltéve hogy az alakzat nem egyetlen pont), ha léteznének n és m természetes számok, hogy n/m*alfa=180 fok, ahol m páratlan (tehát nem kell, hogy alfa osztója legyen 180-nak, mint ahogy Lórántfy áll1totta).
|
| Előzmény: [1652] Matroz, 2012-02-12 11:31:06 |
|
|
| [1668] jenei.attila | 2012-02-19 14:27:02 |
 Szerintem teljesen jó a fixpontok bevetése, sőt ezen múlik az állítás igazsága. Az egybevágóság önmagára való folytonos leképezés, ezért van fixpontja (megfelelő alakzat esetén, mint pl. hogy korlátos), és ez a lényeg. Három nem egy ponton átmenő egyenesre való egymás utáni tükrözés pedig nem eltolás, hanem csúsztatva tükrözés, aminek nincs fixpontja. Az eltolás felé pedig azért akarsz elmenni, mert annak sincs fixpontja, következésképpen nem viheti az alakzatot (folytonos módon) önmagába.
|
| Előzmény: [1674] Fálesz Mihály, 2012-02-19 14:04:27 |
|
| [1674] Fálesz Mihály | 2012-02-19 14:04:27 |
 Szerintem nem a fixpontok bevetése a jó irány, hanem a további szimmetriák keresése.
Ha van három olyan tengelyes tükrözés, aminek a tengelye nem megy át egy ponton, akkor ezekből összerakhatunk egy eltolást.
|
| Előzmény: [1667] jenei.attila, 2012-02-19 11:49:47 |
|
| [1667] jenei.attila | 2012-02-19 11:49:47 |
 "most már csak azt kell belátnod, hogy ha van több szimmetriatengelye is az alakzatnak, akkor azoknak is át kell haladniuk az M ponton. "
Szerintem ezzel nem sokat segítettél, ez mindössze egy triviális átfogalmazás. Mivel a síkbeli egybevágóság "megfelelő" alakzatok önmagára való folytonos transzformációja, ezért alkalmazható rá a Brouwer féle fixponttétel. Megfelelő alakzaton korlátos, zárt (kompakt) és egyéb jó tulajdonsággal bíró (mik ezek? segítsetek) síkbeli ponthalmazt értünk. Tehát egy megfelelő alakzat egybevágóságának mindig van fixpontja. Most indirekt tegyük fel, hogy az alakzatnak van három nem egy ponton átmenő, és páronként nem párhuzamos szimmetria tengelye. Ezen tengelyekre vett egymásutáni tükrözés az alakzatnak szintén egybevágósága lenne, de ennek nincs fixpontja (csúsztatva tükrözés, ami egy irányításváltó fixpont nélküli e.v. transzformáció, mint ez közismert), vagyis ellentmond a Brouwer fixponttételnek.
|
| Előzmény: [1653] lorantfy, 2012-02-12 18:52:46 |
|
|
|
| [1664] Jhony | 2012-02-18 22:09:03 |
 - nem igazán talál amit írtál ,mert ez csak az előző angol nyelvű bizonyításnak lenne a folytatása ,vagyis inkább az arra megírt véleményre amit ,,HoA" írt,hogy az n=a+b+1 egyenlet esetében említett a és b természetes számokat nem lehet összekeveni a prímekből kapott a=(p-1)/2 és b=(k-1)/2 esetében ,na igen ,ha p és k ,2 -nél nagyobb prímeket használunk . - remélhetőleg érthetőbb lesz - ... egyébként meg nem értem mi vagy inkább miért nem érthető ?
- azért köszönöm a hozzászólásokat és még számítok rájuk a továbbiakban is - remélhetőleg számíthatok - köszönöm
|
| Előzmény: [1662] Róbert Gida, 2012-02-18 20:59:08 |
|
| [1663] Maga Péter | 2012-02-18 21:06:53 |
 A Goldbach-topikbéli kérésednek eleget téve megpróbáltam elolvasni ezt az új bizonyítást, de nem sikerült. Sajnos egy hangot sem értek belőle. Nem értem, mit szeretnél kihozni, mi az, amit már tudunk, mi mit jelöl...:S
|
| Előzmény: [1657] Jhony, 2012-02-18 16:13:05 |
|
| [1662] Róbert Gida | 2012-02-18 20:59:08 |
 Kihámoztam a bizonyításodat, és az állításodat. Persze a Goldbach sejtést szeretnéd bizonyítani, ezzel nincs is baj, nézve, hogy az aktív fórumozók fele itt ezt szeretné bizonyítani. De a 7 soros teljes indukciós bizonyítás kicsit pofátlan, nos nem minden 1-nél nagyobb páratlan szám prím, hogy mondjak egy ilyet például a 9. Itt bukik meg a bizonyításod.
|
| Előzmény: [1661] Jhony, 2012-02-18 20:09:11 |
|
| [1661] Jhony | 2012-02-18 20:09:11 |
 - bármelyik n-re létezik egy a = (x - 1)/2 és egy b = (y - 1)/2" - igen értem,csak,hhogy ez előőtt ,ha megnézed van még az,hogy ,,bizonyítsuk be ... " - nos , így is egyértelmű lenne,hogy minden n -re létezik egy a és egy b ,mire az n=a+b+1 igaz ?
- válaszodért köszönet !
|
| Előzmény: [1658] Róbert Gida, 2012-02-18 17:17:45 |
|
|



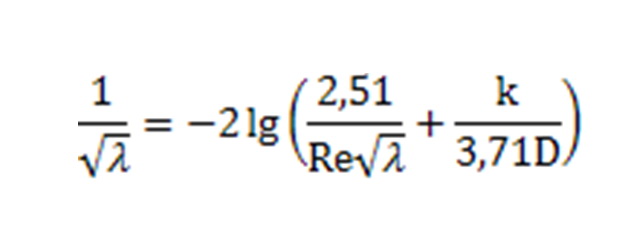


 egy paraméter? Valós? Pozitív? 1-nél nagyobb?
egy paraméter? Valós? Pozitív? 1-nél nagyobb? 
 ? (Különben a függvény nem is invertálható mindenhol.)
? (Különben a függvény nem is invertálható mindenhol.) 





