| [1898] Inverz | 2013-10-11 11:37:18 |
 Egy feladat megoldásában szeretnék segítséget kérni. Az 1976-os matematika OKTV 2. fordulójában az 1. feladat volt a 3. kategóriás diákoknak: Adott egy háromszög. Határozzuk meg a belsejében - esetleg valamelyik oldalán - azt a pontot, amelynek az oldalakra vonatkozó tükörképei által meghatározott háromszög területe maximális!
|
|
|
|
|
| [1894] w | 2013-10-05 22:43:17 |
 Ha valaki talál hibát, szóljon, még kezdő vagyok ebben a műfajban.
Nézzük először racionális számok esetén.
Legyenek a számok (bővített nevezővel): 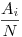 i=1,2,...,n. Ezekhez egy olyan d-t fogunk megadni, melyre i=1,2,...,n. Ezekhez egy olyan d-t fogunk megadni, melyre 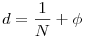 . A . A  >0 számot később fogjuk megadni. >0 számot később fogjuk megadni.
Ugyanis ekkor 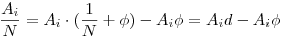 . Azt szeretnénk, hogy . Azt szeretnénk, hogy 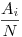 mod d, azaz d-Ai mod d, azaz d-Ai akármilyen közel legyen a d-hez, vagyis akármilyen közel legyen a d-hez, vagyis
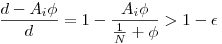
akármilyen kicsi  >0 esetén fennállhasson, alkalmas >0 esetén fennállhasson, alkalmas  esetén. Azaz minden pici esetén. Azaz minden pici  -hoz létezik olyan -hoz létezik olyan  , hogy ... Kifejezzük , hogy ... Kifejezzük  -t: -t:
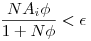
NAi < < + + N N
N (Ai- (Ai- )< )<
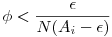
Tehát ekv. egyenlőtl. miatt minden  -hoz van olyan -hoz van olyan  , hogy. Ugyanis véges sok egyenlőtlenséget vezettünk le, i=1,2,...,n-re. , hogy. Ugyanis véges sok egyenlőtlenséget vezettünk le, i=1,2,...,n-re.
Például, ha kapom, hogy 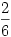 , , 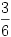 , , 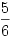 , , 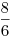 , akkor mondjuk , akkor mondjuk  =0.1-hez =0.1-hez  =0,002 jó választás lesz. =0,002 jó választás lesz.
Amikor irracionális számokkal dolgoztam, akkor iszonyatos pontossággal közelítek. Azaz, veszek akármilyen nagy pontosságot minden ai esetén --> pi/qi rac. számok, de ezek pedig a nevezőket bővítve Ai/(lkkt(qi)) alakúak lesznek, amire lezúzom a fenti számolást. Mivel nagyon pontos vagyok, ezért ez a közelítés elhanyagolható  és és  -hez képest. -hez képest.
|
| Előzmény: [1891] Sinobi, 2013-10-05 20:46:03 |
|
|
| [1892] Róbert Gida | 2013-10-05 20:54:21 |
 Amit te írsz az egy x-re működik. Több x-nél, már lehetséges, hogy a nagyon jól közelítő nevezők teljesen mások, nincs egy nagyon jól közelítő azonos nevező.
Szimultán approximációnak nevezik a problémát, lásd http://www.shunjiito.com/paper/49109yasutomi1030.pdf (introduction első 5 sora).
ezzel (az egyébként trivi) állítással úgy nézem, hogy 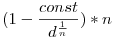 jön ki jobb oldalra az eredeti (n-1) helyett.. (itt a konstans már csak n-től függ). Amiben kell még szórakozni az eredeti bizonyításnál, hogy neked az kell, hogy jön ki jobb oldalra az eredeti (n-1) helyett.. (itt a konstans már csak n-től függ). Amiben kell még szórakozni az eredeti bizonyításnál, hogy neked az kell, hogy  i=d*xi-pi nem csak, hogy kicsi, hanem még negatív is (itt pi egész). i=d*xi-pi nem csak, hogy kicsi, hanem még negatív is (itt pi egész).
|
| Előzmény: [1890] w, 2013-10-05 14:30:26 |
|
|
| [1890] w | 2013-10-05 14:30:26 |
 Szerintem igaz lesz. Tehát az a kérdés, hogyha a1,a2,...,an>0 valós számok, létezik-e olyan d>0 valós, mellyel
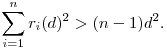
Itt ri(d) [0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d) [0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d)  i=1,2,...,n. i=1,2,...,n.
Most ezt először átrendezzük, hogy átlássuk a szerkezetét:
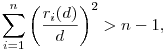
azaz nekünk jó közel kell hoznunk a 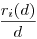 hányadosokat az 1-hez, de úgy, hogy az 1-et még ne érjük el. hányadosokat az 1-hez, de úgy, hogy az 1-et még ne érjük el.
A megoldási ötletem az volna, hogy tfh. 0<a1 a2 a2 ... ... an, és csináljunk racionális approximációt: an, és csináljunk racionális approximációt: 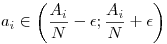 legyen legyen  i, ahol N, Ai egészek. Vegyük i, ahol N, Ai egészek. Vegyük 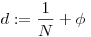 -t, ekkor ai<Aid, ai/d<Ai kellene nekünk, ahol ai/d nagyon közel van Ai-hez. De -t, ekkor ai<Aid, ai/d<Ai kellene nekünk, ahol ai/d nagyon közel van Ai-hez. De 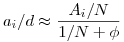 , így ez talán jó lesz, hisz , így ez talán jó lesz, hisz  , , >0 akármilyen kicsi, de egymáshoz képest akármilyen nagy. (Rendesen le kellene tisztítani határértékügyileg, ez még elvi hibás is lehet.) >0 akármilyen kicsi, de egymáshoz képest akármilyen nagy. (Rendesen le kellene tisztítani határértékügyileg, ez még elvi hibás is lehet.)
|
| Előzmény: [1888] Sinobi, 2013-10-05 13:15:24 |
|
|
| [1888] Sinobi | 2013-10-05 13:15:24 |
 Igaz-e, hogy minden nemnegatív a1, a2, ... an valós számok esetén létezik olyan d valós szám, hogy 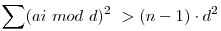 ? (a modulo pozitív értéket ad vissza). Ebből már következne egy másik állítás, amiből egy megint másik, amiből a feladat, de ez ehhez hozzá se tudok nyúlni, nem is látszik igaznak :( Van valakinek ötlete? Másik becslése, ellenpéldája, stb? ? (a modulo pozitív értéket ad vissza). Ebből már következne egy másik állítás, amiből egy megint másik, amiből a feladat, de ez ehhez hozzá se tudok nyúlni, nem is látszik igaznak :( Van valakinek ötlete? Másik becslése, ellenpéldája, stb?
|
|
| [1887] koma | 2013-10-03 22:47:30 |
 köszi mindenkinek a hozzászólását, tényleg nem volt egy "nehéz" feladat, de valahogyan nem jöttem mégsem rá... sebaj, most már okosabb lettem, köszönöm:)
|
|
| [1886] w | 2013-10-03 20:04:50 |
 Ez igazából ugyanaz a megoldás: a3-3ab=35, ab=30 után a3=(x+y)3=125, x+y=5. Köszi viszont, hogy leírtad. (Direkt azért úgy mutattam be, mert kicsit általánosabb, pl. alkalmas az x+y=3, x4+y4=17 egyenletrendszer megoldására is.)
Fálesz Mihálynak is köszönöm a megoldási ötletét/módszerét, nagyon érdekes volt.
|
| Előzmény: [1884] Alekszandrov, 2013-10-03 11:20:52 |
|
|
| [1884] Alekszandrov | 2013-10-03 11:20:52 |
 Van másik megoldás is, nem kell ehhez a és b! :-)
A második egyenletet szorozd meg hárommal, majd add össze az elsővel, így x+y köbe egyenlő 125-tel, tehát x+y=5. Majd a második egyenletet szorzattá alakítva, az x+y helyébe beírva az 5-öt, kapjuk: xy=6 Ez a két egyenlet már ránézésre is megoldható!
|
| Előzmény: [1883] koma, 2013-09-30 10:02:34 |
|
|
| [1882] w | 2013-09-29 22:42:37 |
 Szia Koma!
Az 1) feladatod klasszikus példa az ún. elemi szimmetrikus polinomok alkalmazására. Tehát az ilyen szimmetrikus kifejezéseket ki lehet fejezni a:=x+y és b:=xy segítségével: 35=x3+y3=(x+y)(x2-xy+y2)=(x+y)[(x+y)2-3xy]=(x+y)3-3xy(x+y)=a3-3ab és 30=x2y+xy2=xy(x+y)=ab. Innen már nem olyan nehéz befejezni.
2) 3) Vedd észre, hogy a2 0 és |a| 0 és |a| 0, ahol egyenlőség épp akkor áll fenn, ha a=0. 0, ahol egyenlőség épp akkor áll fenn, ha a=0.
|
| Előzmény: [1881] koma, 2013-09-29 20:13:57 |
|
| [1881] koma | 2013-09-29 20:13:57 |
 Az alábbi feladatok megoldásában kérném a segítségeteket:
1,Oldjuk meg az alábbi egyenletrendszert! x3+y3=35, b, x2y+y2x=30
ugyebár a= (x+y)(x2-xy+y2) b= xy(x+y), de hogyan tovább?
2, (x2-1)2+(x4-1)2=0 látom, hogy másodfokú egyenletre vezet, de nem látom a megoldását
3, abs (x+y-13) + abs (y-z-5) abs (y-z-2) =0
nagyon szépen köszönöm előre is a segítséget, és további szép estét kívánok!
|
|
|
|
| [1878] koma | 2013-09-28 18:59:33 |
 Sziasztok, akadt két problémám, nagyon megköszönném, ha valaki kisegítene.:)
1, Határozza meg az a1=1,an+1=2an (n term szám) rekurzív sorozat képletét.
2,Mutassuk meg, hogy az alábbi rekurzív sorozat monoton csökkenő: a1=2,a2=1,an+1=5an-6an-1,(n 2) 2)
köszönöm szépen a segítséget.
|
|
| [1877] bianka | 2013-09-28 10:25:42 |
 szia!
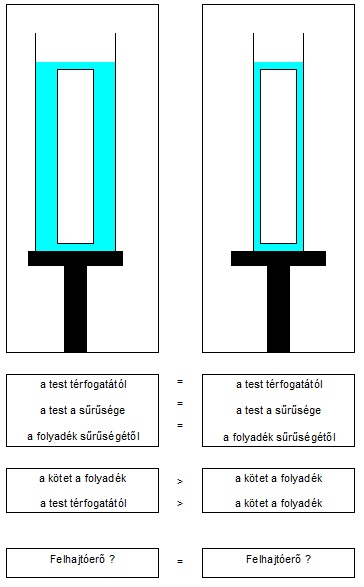
egy gyors kérdés (skicc)
köszi! ...bianka
|
 |
|
| [1876] gyula60 | 2013-09-17 20:11:06 |
 Javaslom az 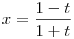 helyettesítés alkalmazását, amely után a kanonikus alakra hozás jobban megvalósítható. helyettesítés alkalmazását, amely után a kanonikus alakra hozás jobban megvalósítható.
A keresett primitív fügvényt a következő két f1(x) és f2(x) függvény összege állítja elő:
![f_1(x)=-\frac{1}{\sqrt2}arc\tg\bigg[\frac{\root\of{x^2+x+1}}{\sqrt2(x-1)}\bigg]](keplet.cgi?k=7F83EA544685A758) , ,
![f_2(x)=-\frac{1}{\sqrt6}\ln\bigg[\frac{\sqrt2(x+1)-\root\of{3(x^2+x+1)}}{\root\of{(x^2-x+1)}}\bigg]](keplet.cgi?k=B1C572E2B7464A7A) . .
|
| Előzmény: [1874] juantheron, 2013-09-02 21:12:42 |
|
|
|





 >0 számot később fogjuk megadni.
>0 számot később fogjuk megadni.  >0 esetén fennállhasson, alkalmas
>0 esetén fennállhasson, alkalmas 
 i=q*xi-pi akart lenni, és persze nálam is d alakja speciális
i=q*xi-pi akart lenni, és persze nálam is d alakja speciális  [0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d)
[0;d) az a valós szám, melyhez létezik k egész szám, mellyel ai=kd+ri(d)  i=1,2,...,n.
i=1,2,...,n.  a2
a2

 0 és |a|
0 és |a|
