| [2189] marcius8 | 2018-10-23 14:57:32 |
 Az könnyen látható, hogy a \(\displaystyle q_1\) és \(\displaystyle q_2\) kvaterniókhoz létezik olyan \(\displaystyle q\) kvaternió, amelyre teljesül, hogy a \(\displaystyle q_1\) kavternió a \(\displaystyle q\) kvaterniónak valamilyen (egész) kitevőjű hatványa, és a \(\displaystyle q_2\) kvaternió a \(\displaystyle q\) kvaterniónak valamilyen (egész) kitevőjű hatványa, akkor \(\displaystyle q_1*q_2=q_2*q_1\) egyenlet teljesül. Igaz-e ennek az állításnak a megfordítása?
|
|
| [2188] marcius8 | 2018-07-21 16:55:42 |
 \(\displaystyle n\) darab egymással szabályos ötszöget feldarabolunk az átlói mentén. Így keletkezik \(\displaystyle 5n\) darab egyenlő szárú háromszög, melyeknek szögei 36°, 36°, 108°, keletkezik \(\displaystyle 5n\) darab egyenlő szárú háromszög, melyeknek szögei 72°, 72°, 36°, és keletkezik \(\displaystyle n\) darab kisebb, egymással egybevágó szabályos ötszög. Milyen \(\displaystyle n\) esetén rakható össze a keletkezett síkidomokból mindegyiket pontosan egyszer felhasználva egy nagyobb szabályos ötszög?
|
|
|
|
| [2185] marcius8 | 2018-07-02 10:55:54 |
 Végül is a primnégyzetek reciprokösszege csak egy másik végtelen összeggel lett felírva, amelynek értéke el lett nevezve. Ez nagyjából annak a beismerése, hogy igazából semmit sem tudunk erről az összegről. De a [2183] kérdés nagyon jó!!!! A [2184] válasz meg érdekes. A [2183] kérdés annyira tetszett nekem, hogy ezzel kapcsolatban nekem is eszembe jutottak a következő kérdések:
Mit tudunk a \(\displaystyle 4k+1\) alakú pozitív prímek reciprokösszegéről? Mit tudunk a \(\displaystyle 4k-1\) alakú pozitív prímek reciprokösszegéről?
Mit tudunk a \(\displaystyle 6k+1\) alakú pozitív prímek reciprokösszegéről? Mit tudunk a \(\displaystyle 6k-1\) alakú pozitív prímek reciprokösszegéről?
|
| Előzmény: [2184] Lóczi Lajos, 2018-07-01 09:45:07 |
|
|
| [2183] Bátki Zsolt | 2018-06-30 15:55:57 |
 Mint tudjuk a természetes számok reciprokának az összege végtelen (divergens a sor) A prímszámokra is végtelen: azaz sum (1/p) nagyon soknál is több. Sum (1/i*i) Négyzetszámok reciprok összege (pi*pi/6, Euler alapján) véges.
De mennyi sum (1/(p*p)) azaz:prímek négyzetének reciprok összege mennyi? nem találtam erre az interneten. Próbáltam számolni de nem sokra jutottam a sejtésben, hogy mennyi. Írok rá programot, de az nem hozza ki a formulát, ha van egyáltalán. Köszi a segítségetek. 1/(2*2)+1/(3*3)+1/(5*5)+1/(7*7)+1/(11*11)+1/(13*13)+1/(17*17) =0.439...
|
|
| [2182] Erben Péter | 2018-06-30 14:00:50 |
 Jobban átgondolva a hivatkozott elemibb megoldást, látok benne egy hiányosságot (abban az esetben, amikor a legkisebb háromszög valamelyik szélen van), és nem vagyok biztos benne, hogy ez (egyszerűen) javítható.
|
| Előzmény: [2181] Erben Péter, 2018-06-30 11:08:13 |
|
| [2181] Erben Péter | 2018-06-30 11:08:13 |
 Ha jól értem, háromszögekre először W. T. Tutte bizonyította, hogy nem lehetséges ilyen felbontást csinálni. (Dissections into Equilateral Triangles, in. The Mathematical Gardner (1981))
Itt van egy elemibb megoldás, ami analóg azzal, ahogy kockákra szokás bizonyítani a lehetetlenséget.
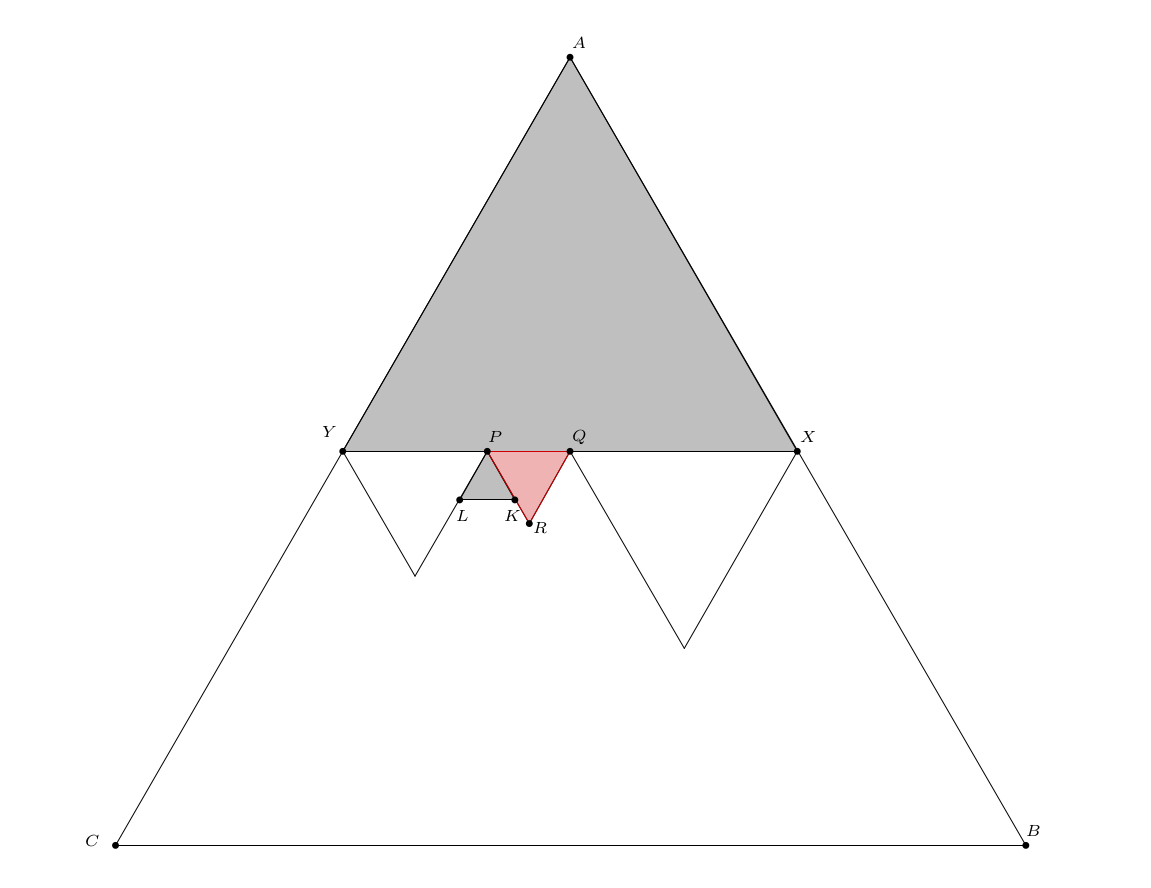
Legyen az \(\displaystyle ABC\) szabályos háromszög \(\displaystyle A\) csúcsát lefedő háromszög \(\displaystyle AXY\). Az \(\displaystyle XY\) oldalt különböző hosszú háromszög oldalak fedik, ezek közül a legrövidebb \(\displaystyle PQ\) (\(\displaystyle P\) vagy \(\displaystyle Q\) eshet az eredeti háromszög oldalára is), és a szabályos háromszög \(\displaystyle PQR\).
A \(\displaystyle P\) és \(\displaystyle Q\) csúcsú ,,felfelé álló'' háromszögek közül legalább az egyik kisebb, mint \(\displaystyle PQR\), különben ezek \(\displaystyle R\)-nél egymásba csúsznának.
Legyen mondjuk \(\displaystyle PKL\) a kisebb. Most a \(\displaystyle PKL\) háromszög átveszi \(\displaystyle AXY\) szerepét, és megint fogunk találni egy \(\displaystyle PKL\)-nél kisebb ,,felfelé álló'' szürke háromszöget a felbontásban.
Mivel a leírt logika tetszőlegesen sokáig folytatható, nem állhat véges sok háromszögből a felbontás.
|
 |
| Előzmény: [2180] marcius8, 2018-06-23 20:14:32 |
|
| [2180] marcius8 | 2018-06-23 20:14:32 |
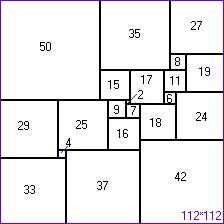
 Arie Duijvestijn (remélem, jól írom a nevet) holland matematikus egy négyzetet felbontott különböző méretű négyzetekre. (Lásd: ábra). Vajon egy szabályos háromszöget is fel lehet bontani különböző méretű szabályos háromszögekre?
|
 |
|
| [2179] marcius8 | 2018-02-23 11:18:54 |
 Középiskolában tanítják (tanítom) a visszatevés nélküli mintavételt és a visszatevéses mintavételt. A visszatevés nélküli mintavétel azt jelenti, hogy egy alapsokaságból egyszerre kiveszek valamennyi elemet, és a kivett elemeket tekintem egy mintának. A visszatevéses mintavétel azt jelenti, hogy az alapsokaságból valamennyiszer véletlenszerűen kiveszek egy elemet, és a kivett elemet mindig visszateszem. És azt is tudjuk, hogy a reprezentatív minta valószínűsége a legnagyobb, mint a visszatevéses mintavétel esetében, mind a visszatevés nélküli mintavétel esetében. DE!!! Tekintsük a következő példát:
Van 10 darab fehér golyó, 20 darab világosszürke golyó, 30 darab sötétszürke golyó, 40 darab fekete golyót. Most úgy készítek egy 50 elemű mintát, hogy kiveszek 5 darab golyót, megnézem ezt az 5 golyót, visszateszem az alapsokaságba, elkeverem az alapsokaságot, megint kiveszek 5 darab golyót,.... ezt 10-szer csinálom meg. Tulajdonképpen ez is visszatevéses mintavétel, csak a mintavétel 5-ösével történik. Ilyenkor milyen összetételű minta a legvalószínűbb, és mennyi ennek a valószínűsége?
|
|
|
| [2177] marcius8 | 2018-02-13 13:18:31 |
 Keresem az \(\displaystyle a_{n+1}=\sqrt{2a_n+3}\), \(\displaystyle a_1=4\) sorozat explicit alakját. Minden segítséget előre is köszönök! Amit tudok, az hogy a sorozat határértéke 3, és szigorúan monoton csökkenő. Tisztelettel: Bertalan Zoltán.
|
|
| [2174] Fálesz Mihály | 2018-02-02 10:07:26 |
 A két példád között különbség van, és a lényeg a kiválasztási axióma szerepe.
A transzcendens számok halmaza egy konkrét, a kiválasztási axióma használata nélkül is jól megadható halmaz. Az \(\displaystyle \mathbb{R}\)-rel való megfelelést sem nehéz kitalálni, ehhez elég az algebrai számok egy felsorolása, de még felsorolás nélkül sem nehéz.
A bázis esetében a nehézség nem a bijekcióval kezdődik, hanem azzal, hogy melyik bázisról van szó a \(\displaystyle 2^{2^{\aleph_0}}\) lehetőség közül. Azt, hogy egyáltalán létezik bázis, a Zorn-lemmából, vagy a kiválasztási axióma valamelyik más ekvivalens formájából szoktuk bizonyítani. Ha mondasz egy konkrét bázist, én majd mondok hozzá egy konkrét bijekciót az \(\displaystyle \mathbb{R}\)-rel... :-)
|
| Előzmény: [2173] marcius8, 2018-02-01 08:25:51 |
|
| [2173] marcius8 | 2018-02-01 08:25:51 |
 Nem is ezzel van a problémám, hogy oda-vissza létezik kölcsönösen egyértelmű megfeleltetés a valós számok halmaza és egy adott kontinuum-számosságú halmaz között. Hanem azzal, hogy egy adott kontinuum-számosságú halmaz és a valós számok halmaza között nem tudok egy konkrét megfeleltetést létesíteni.
Pl. A transzcendens számok kontinuum-számosságú halmazt alkotnak. Adjunk meg konkrétan egy kölcsönösen egyértelmű megfeleltetést a transzcendens számok és a valós számok között.
Pl. Tekintsük a valós számokat mint a racionális számok feletti vektorteret. Ekkor ennek a vektortérnek van bázisrendszere, és ennek a bázisrendszernek az elemszáma kontinuum-számosságú. Adjunk meg egy kölcsönösen egyértelmű megfeleltetést ezen bázisrendszer és a valós számok között.
|
| Előzmény: [2172] Fálesz Mihály, 2018-01-30 22:30:14 |
|
| [2172] Fálesz Mihály | 2018-01-30 22:30:14 |
 Tehát, ha van egy kontinuum számosságú \(\displaystyle K\) halmazunk, akkor van \(\displaystyle f:\mathbb{R}\to K\) bijekció is.
Az \(\displaystyle \mathbb{R}\)-et \(\displaystyle n\) kontinuum számosságú részre osztjuk — mondjuk \(\displaystyle n\) diszjunkt intervallumra: \(\displaystyle \mathbb{R}=R_1\cup\dots\cup R_n\). Ezután részhalmazokat visszaképezzük az eredeti halmazba:
\(\displaystyle K = f(R_1) \cup \ldots \cup f(R_n). \)
|
| Előzmény: [2171] marcius8, 2018-01-30 08:28:08 |
|
|
|
| [2169] marcius8 | 2018-01-29 09:24:39 |
 Nekem elég, ha egy ellenség által megadott kontinuumszámosságú halmazt egy konkrét algoritmussal két kontinuumszámosságú részre osztjuk. (Nyilván a két rész metszete üres halmaz, és a két rész uniója az ellenség által megadott kontinuumszámosságú halmaz.)
|
| Előzmény: [2165] Fálesz Mihály, 2018-01-10 07:59:00 |
|
| [2168] marcius8 | 2018-01-21 08:41:51 |
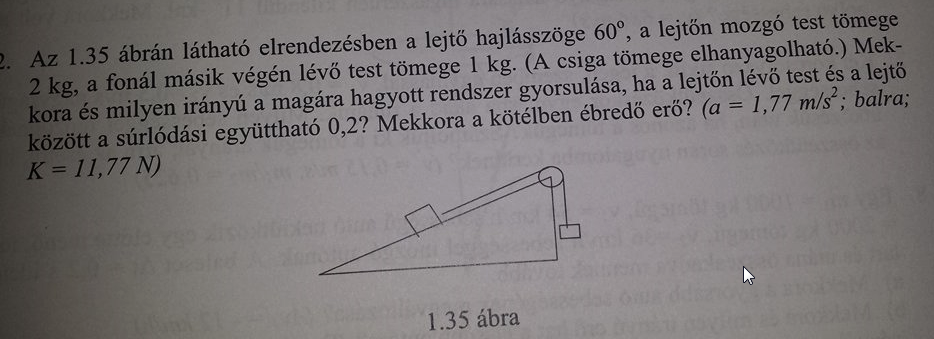
 \(\displaystyle m_1=2\rm{kg}\), \(\displaystyle m_2=1\rm{kg}\), \(\displaystyle g=10\rm{méter/sec^2}\), \(\displaystyle \alpha=60°\), \(\displaystyle \mu=0,2\).
Legyen \(\displaystyle F_{tartó}\) a lejtő által kifejtett, az \(\displaystyle m_1\) testre ható tartóerő, ez az erő a lejtő felületére merőleges, és az ábra szerint ferdén balra és felfelé mutat. Az \(\displaystyle m_1\) testre hat az \(\displaystyle G_1=m_1g\) súlyerő, ennek az iránya függőlegesen lefelé mutat. Ezt az erőt érdemes a lejtővel párhuzamos \(\displaystyle G_{1párh}=m_1g*\sin(\alpha)\) és \(\displaystyle G_{1mer}=m_1g*\cos(\alpha)\) erőkre bontani. Az \(\displaystyle m_1\) testre hat még a \(\displaystyle K\) kötélerő, ennek iránya a lejtővel párhuzamos, és az ábra szerint jobbra és felfelé mutat a csiga irányába. Az \(\displaystyle m_1\) testre hat még az \(\displaystyle S\) súrlódási erő, amelynek iránya a lejtővel párhuzamos, az \(\displaystyle m_1\) test mozgásával ellentétes. Az \(\displaystyle m_2\) testre hat a \(\displaystyle G_2=m_2g\) súlyerő, ennek iránya függőlegesen lefelé mutat. Az \(\displaystyle m_2\) tömegű testre hat a \(\displaystyle K\) kötélerő, ennek iránya függőlegesen felfelé mutat.
Az \(\displaystyle m_1\) tömegű test a lejtőre merőlegesen nem mozog, ezért a rá ható és a lejtőre merőleges erők kiegyenlítik egymást, azaz \(\displaystyle F_{tartó}=G_{1mer}\) azaz \(\displaystyle F_{tartó}=m_1g*\cos(\alpha)\). A súrlódási erő definíciója miatt \(\displaystyle S=\mu*F_{tartó}=\mu*m_1g*\cos(\alpha)\) Tegyük fel, hogy az \(\displaystyle m_1\) test a lejtőn felfelé az \(\displaystyle m_2\) test függőlegesen lefelé gyorsul. Ekkor az \(\displaystyle m_1\) testre ható \(\displaystyle S\) súrlódási erő iránya a lejtőn lefelé mutat. A két test gyorsulásának nagysága egyenlő, legyen \(\displaystyle a\) a két test gyorsulásának nagysága.
Alkalmazva Newton II. törvényét a két testre:
\(\displaystyle m_1a=K-G_{1párh}-S=K-m_1g*\sin(\alpha)-\mu*m_1g*\cos(\alpha)\)
\(\displaystyle m_2a=G_2-K=m_2g-K\)
Ekkor \(\displaystyle a=-3,1068\rm{méter/sec^2}\) és \(\displaystyle K=13,1068\rm{Newton}\) adódik. Mivel \(\displaystyle a\) értéke negatív, ezért hibás volt az a feltételezés, hogy az \(\displaystyle m_1\) test a lejtőn felfelé, az \(\displaystyle m_2\) test a lejtőn lefelé gyorsul.
Most tegyük fel, hogy az \(\displaystyle m_1\) test a lejtőn lefelé az \(\displaystyle m_2\) test függőlegesen felfelé gyorsul. Ekkor az \(\displaystyle m_1\) testre ható \(\displaystyle S\) súrlódási erő iránya a lejtőn felfelé mutat. A két test gyorsulásának nagysága egyenlő, legyen \(\displaystyle a\) a két test gyorsulásának nagysága.
Alkalmazva Newton II. törvényét a két testre:
\(\displaystyle m_1a=K-G_{1párh}-S=m_1g*\sin(\alpha)-K-\mu*m_1g*\cos(\alpha)\)
\(\displaystyle m_2a=G_2-K=K-m_2g\)
Ekkor \(\displaystyle a=1,7735\rm{méter/sec^2}\) és \(\displaystyle K=11,7735\rm{Newton}\) adódik.
|
| Előzmény: [2167] shadow, 2018-01-18 22:06:00 |
|
| [2167] shadow | 2018-01-18 22:06:00 |
 Sziasztok!
Már nagyon régen volt, és a gyakorlatvezetőim sem a legjobbak voltak. Az rémlik, hogy két komponensre kellene bontanom az erőket de már nem tudom hogyan induljak neki. Esetleg valaki tud segíteni?
|
 |
|
| [2165] Fálesz Mihály | 2018-01-10 07:59:00 |
 Csatlakozva jonashoz, a kérdésed úgy kezdődött, hogy "hogyan lehet egy kontinuum számosságú halmazt..."
Tehát a játékban kapunk az ellenségünktől egy halmazt, amiről tudni véli, de inkább be tudja bizonyítani, hogy "kontinuum számosságú", és egy \(\displaystyle n\) pozitív egészt. Nekünk az a feladatunk, hogy a halmazt valami algoritmussal \(\displaystyle n\) részre osszuk.
A kérdés: annak bizonyítása, hogy a halmaz kontinuum számosságú, nem biztosít automatikusan (például a Cantor-Schröder-Bernstein tétel segítségével) egy bijekciót valamilyen ismert, kontinuum számosságú halmazzal?
|
| Előzmény: [2162] marcius8, 2018-01-09 20:02:28 |
|
| [2164] Fálesz Mihály | 2018-01-10 07:43:04 |
 Megfelelteted a (legyen mondjuk \(\displaystyle H\)) halmazt az \(\displaystyle [0,n)\) intervallumnak vagyis veszel egy \(\displaystyle f:[0,n)\to H\) bijekciót. A \(\displaystyle [0,n)\) intervallum a szintén kontinuum számosságú \(\displaystyle [0,1),\ldots,[n-1,1)\) intervallumok uniója; ezeket külön-külön is képezheted a \(\displaystyle H\) halmazba:
\(\displaystyle
H =
f\big([0,n)\big) =
f\big([0,1)\big) \cup\ldots\cup f\big([n-1,n)\big).
\)
Véges sok helyett kontinuum sok résszel is megy: a kontinuum számosságú sík felbontható kontinuum sok párhuzamos egyenes uniójára.
|
| Előzmény: [2158] marcius8, 2018-01-06 18:23:36 |
|
| [2163] jonas | 2018-01-10 01:01:48 |
 Azt, hogy egy halmaz kontinuum számosságú, többé-kevésbé úgy definiáljuk, hogy van egy bijekció valamilyen rögzített kontinuum számosságú halmazra, mondjuk a természetes számok halmazának a hatványhalmazára. Ha be szeretnéd bizonyued tani egy konkrét halmazról, hogy tényleg kontinuum számosságú, akkor többnyire a Schröder-Bernstein tételt a legkönnyebb fölhasználni. Ez gyakran kikerülhető lenne, de könnyebb egyszer bebizonyítani azt a tételt, mint minden példához újabb konstrukciókat keresni.
|
| Előzmény: [2162] marcius8, 2018-01-09 20:02:28 |
|
| [2162] marcius8 | 2018-01-09 20:02:28 |
 Bármilyen meglepő, én is pont egy ilyen módszerre gondoltam. DE! konkrétan egy ilyen "univerzális" megfeleltetést még nem tudtam találni, ami bármilyen adott kontinuum-számosságú halmaz esetén működne.
|
| Előzmény: [2160] Sirpi, 2018-01-09 09:23:30 |
|











