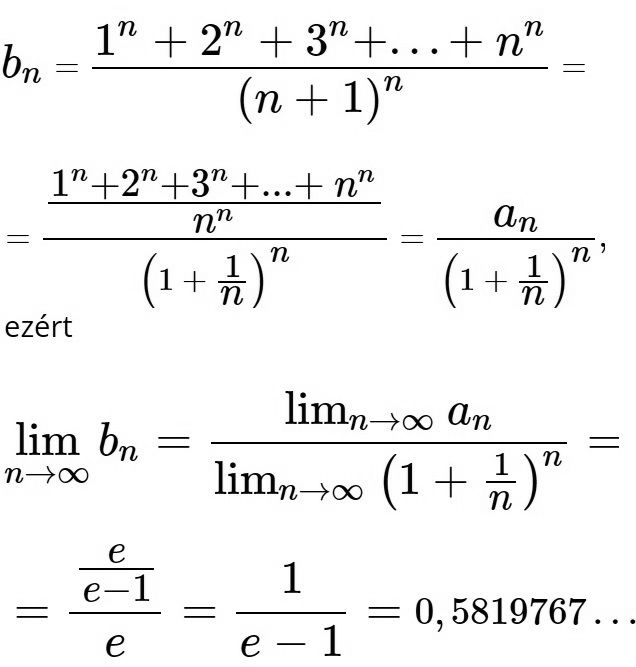| [2306] hanyforint | 2023-08-16 19:11:59 |
 Találtam egy angol nyelvű pdf-et erről, ami több oldalon keresztül elmagyarázza ezt, itt: "https://web.northeastern.edu/seigen/11Magic/StebbinsStack/Si Stebbins Stack - from Numericana dot com.pdf"
|
| Előzmény: [2303] marcius8, 2023-07-19 18:45:26 |
|
| [2305] nadorp | 2023-08-09 15:15:34 |
 Írjuk fel a kör kerületére az 1,2...,52 számokat és tegyük a számok mellé a kártyákat a sor definíciója szerint úgy, hogy az 1 mellett legyen a pikk ász.
Ha \(\displaystyle 1\leq i\leq j\leq52\), akkor az \(\displaystyle i\)-dik és \(\displaystyle j\)-dik lap távolsága legyen \(\displaystyle d=\min(j-i,52+i-j)\) ( a nem hosszabb íven levő intervallumot vesszük)
Minden lapot egyértelműen meghatároz egy \(\displaystyle (a,b)\) számpár (\(\displaystyle 0\leq a\leq3,0\leq b\leq12\)), ahol a="szín", b="érték-1" (Most a színekre pikk=0,kőr=1,treff=2,káró=3)
Ekkor a pikk ász a \(\displaystyle (0,0)\) és ha az \(\displaystyle n\)-dik lap az \(\displaystyle (a,b)\), akkor:
\(\displaystyle n-1\equiv a\mod(4)\)
\(\displaystyle 3(n-1)\equiv b\mod(13)\)
Ismert, hogy adott \(\displaystyle (a,b)\) esetén a fenti kongruencia rendszernek egyértelmű megoldása van \(\displaystyle n\)-re \(\displaystyle \mod(52)\), és különböző \(\displaystyle (a,b)\) számpárra - melyek megfelelnek a fenti feltételnek - különböző \(\displaystyle n\)-et kapunk.
Ha most adott két lap \(\displaystyle (a_1,a_2)\) és \(\displaystyle (b_1,b_2)\), melyek az \(\displaystyle n_1\)-dik illetve \(\displaystyle n_2\)-dik helyen vannak, akkor a fentiek szerint
\(\displaystyle n_1-n_2\equiv a_1-a_2\mod(4)\)
\(\displaystyle 3(n_1-n_2)\equiv b_1-b_2\mod(13)\)
——
\(\displaystyle 13(n_1-n_2)\equiv 13(a_1-a_2)\mod(52)\)
\(\displaystyle 12(n_1-n_2)\equiv 4(b_1-b_2)\mod(52)\)
——
\(\displaystyle n_1-n_2\equiv 13(a_1-a_2)-4(b_1-b_2)\mod(52)\)
Innen már látszik a módszer a távolság kiszámítására:
Kiszámoljuk \(\displaystyle 13(a_1-a_2)-4(b_1-b_2)\) értékét és vesszük az 52-es nemnegatív maradékát. Ha ez \(\displaystyle d\) , akkor a távolság \(\displaystyle \min(d,52-d)\)
|
| Előzmény: [2303] marcius8, 2023-07-19 18:45:26 |
|
| [2304] marcius8 | 2023-07-19 18:49:50 |
 az előző hozzászólásomhoz ábrát csatolok, hátha így érthetőbb lesz a Si Stebbins sorrend
|
 |
|
| [2303] marcius8 | 2023-07-19 18:45:26 |
 Egy matekos kérdésem lenne, de nem boldogulok vele. A römi kártyák (52 lapból álló jokerek nélküli francia kártya) egy speciális sorrendjéről van szó, ezt a sorrendet SI STEBBINS sornak nevezik. Lényege: az ábrán látható körben óramutató járásával megegyező irányban a lapok színei periodikusan követik egymást (most pl. pikk, kőr, treff, káró), és bármelyik lap értéke mindig 3-mal több mod 13, mint az előtte levő lap értéke. Előnye ennek a sorrendnek, hogy valójában nincs vége, azaz a kártyacsomag utolsó lapja után következik a kártyacsomag első lapja... A probléma a következő: Két lap színének és értékének ismeretében hogyan lehet gyorsan és könnyen kiszámolni a két lap távolságát. Egyszerű képletet keresek. Mindenki segítségét előre is köszönöm.
|
|
|
| [2301] marcius8 | 2023-06-26 20:14:02 |
 Van 20 darab egymástól nem feltétlenül különböző szám. A 20 darab számot tetszőlegesen szétválasztjuk két 10 elemű halmazra. Ezután egy 2 sorból és 10 oszlopból álló táblázat felső sorába beírjuk az egyik 10 elemű halmaz elemeit növekvő (nem csökkenő) sorrendben, a táblázat alsó sorába beírjuk a másik 10 elemű halmaz elemeit csökkenő (nem növekvő) sorrendben Ezután a táblázat minden oszlopában kiszámoljuk az oszlopban levő két szám különbségét (különbség = nagyobb szám - kisebb szám), majd az így kapott különbségeket összeadjuk, így egy eredmény adódik. Bizonyítsuk be, hogy bárhogy is választjuk szét a 20 darab számot két 10 elemű halmazra, a kapott eredmény mindig kiszámolható úgy is, hogy a 10 legnagyobb szám összegéből kivonjuk a 10 legkisebb szám összegét. Mindenki segítségét előre is köszönöm: BZ.
|
|
| [2300] nadorp | 2023-04-30 07:58:43 |
 Szerintem a 1. feladatra a Sylvester-Gallai tétel túl erős, csak akkor kéne, ha azt a gyengébb feltételt vesszük, hogy bármely 3 pont által kifeszített síkra illeszkedik egy tőlük különböző negyedik pont.
Az 1. feladatban válasszunk tetszőleges A,B,C pontokat. Ezek nem kollineárisak, tehát egyértelműen meghatároznak egy S síkot. Ha most veszünk egy, az előző pontoktól különböző P pontot, akkor a feltétel szerint A,B,C és P egy síkon helyezkednek el, de ez a sík tartalmazza az A,B,C pontokat is, tehát meg kell hogy egyezzen S-sel. Tehát a pontok egy síkon vannak.
|
| Előzmény: [2298] Lpont, 2023-04-28 13:26:55 |
|
| [2299] nadorp | 2023-04-29 14:06:04 |
 Bizonyítás teljes indukcióval.
Ha n=3, akkor igaz az állítás, mert ekkor n-3=0 és a háromszögnek nincs átlója.
Ha n=4, igaz az állítás, mert ekkor n-3=1 és mivel egy konvex négyszög 2 átlója metszi egymást, ezért csak egy átlót húzhatunk be.
Legyen \(\displaystyle n\geq5\), \(\displaystyle K_n\) egy n oldalú konvex sokszög és tegyük fel, hogy n-nél kisebb oldalszámú konvex sokszögre igaz az állítás.
Húzzunk be egy tetszőleges \(\displaystyle f\) átlót \(\displaystyle K_n\)-ben. Ekkor a sokszöget egy i oldalú \(\displaystyle K_i\) és egy n+2-i oldalú \(\displaystyle K_{n+2-i}\) konvex sokszögre bontottuk fel \(\displaystyle (3\leq i\leq n-1\)). Nyilvánvaló, hogy ezek után csak olyan átlót húzhatunk be \(\displaystyle K_n\)-ben, mely vagy csak \(\displaystyle K_i\) vagy csak \(\displaystyle K_{n+2-i}\) belsejében halad, ugyanis ellenkező esetben a behúzott átló metszené \(\displaystyle f\)-et. Az indukciós feltevés miatt így legfeljebb összesen
\(\displaystyle i-3+n+2-i-3=n-4\) átlót húzhattunk be.
Ezekhez hozzávéve a \(\displaystyle f\) átlót, kapjuk, hogy \(\displaystyle K_n\)-be is legfeljebb n-3 egymást nem metsző átló húzható be,mely tartalmazza \(\displaystyle f\)-et. A kapott felső érték nem függ i-től (így \(\displaystyle f\)-től sem), tehát \(\displaystyle K_n\)-be is legfeljebb n-3 darab egymást nem metsző átló húzható be.
A kapott felső korlát mindig elérhető, ha egy kijelölt fix csúcsból húzzuk be az összes átlót.
|
| Előzmény: [2297] marcius8, 2023-04-28 09:20:57 |
|
| [2298] Lpont | 2023-04-28 13:26:55 |
 Az 1. feladatra az alábbi - síkbeli - Sylvester-Gallai tétel bizonyításának gondolatmenetét lehet felhasználni a térben is.
Sylvester-Gallai tétel: Adott n>=3 pont a síkon. Ekkor vagy az összes adott pont illeszkedik egy egyenesre, vagy van egy olyan egyenes, amire közülük pontosan kettő illeszkedik!
A tétel bizonyítása az interneten is elérhető több oldalon is.
|
| Előzmény: [2297] marcius8, 2023-04-28 09:20:57 |
|
| [2297] marcius8 | 2023-04-28 09:20:57 |
 Köszönöm a szép megfogalmazásokat. Ilyenkor látom, hogy bár ha tudom a feladat megoldását, vagy legalábbis azt hiszem, hogy tudom a feladat megoldását, még nem biztos, hogy jól le tudom írni. Találkoztam további két feladattal, amelyet tudom, hogy igaz, azt is tudom, hogy miért, de nem tudom szépen megfogalmazni:
1. Adott térben véges sok pont úgy, hogy semelyik három nincs egy egyenesen. Igaz-e, hogy ha bármelyik négy pont illeszkedik egy síkra, akkor az összes pont egy síkon van? Mi a helyzet végtelen sok pont esetén.
2. Igaz-e, hogy egy \(\displaystyle n\) oldalú konvex sokszögbe maximum \(\displaystyle n-3\) átlót lehet behúzni, úgy hogy az átlóknak ne legyen metszéspontjuk?
|
|
| [2296] BerkoErzsebet | 2023-04-28 05:57:12 |
 Egy könyvemből (Matematikai versenytételek) másolok.
II. megoldás: Ha a derékszögű háromszög átfogóját a kisebbik (pontosabban: a másiknál nem nagyobb) befogóval elosztjuk, gyök2-nél nem kisebb hányadoshoz jutunk. Ez abból következik, hogy a<= b esetén c*c=a*a+b*b>=2*a*a, tehát c/a>=gyök2.
Ha a háromszög két oldalát változatlanul hagyjuk, de az általuk közrefogott szöget növeljük, akkor a harmadik oldal is növekszik. Ezért tompaszögű háromszögre, sőt (egy egyenesen elhelyezkedő, csatlakozó szakaszokká) elfajuló háromszögre is kimondhatjuk, hogy legnagyobb oldala a legkisebbel osztva legalább gyök2 értékű hányadost ad.
Elég ezért azt bizonyítanunk, hogy a sík bármely négy pontja között van három olyan, amely derékszögű, tompaszögű vagy elfajuló háromszöget határoz meg. Induljunk ki a sík négy pontjából. Feltehetjük, hogy nincs közöttük három egy egyenesen elhelyezkedő. Tekintsük a négy pont konvex burkát, azaz azt az idomot, amelyet úgy kapunk, hogy a pontok köré fonalat feszítünk. Minthogy a pontok nincsenek mindannyian egy egyenesen, konvex burkuk vagy háromszög, vagy négyszög. Ha a P1P2P3 háromszöghöz jutunk, akkor P4 ennek belsejében van, hiszen három pont nem lehet egy egyenesen. A P4P1, P4P2, P4P3 szakaszok háromszögünket három háromszögre vágják fel. Ezeknek P4-nél elhelyezkedő három szöge együttesen 360 fok, s ezért közöttük tompaszög is van (sőt közülük legalább kettő tompa.) Egy ilyen tompaszög a pontjainkból alakított tompaszögű háromszög szöge. Ha a konvex burok négyszög, akkor ennek szögeiről elmondhatjuk, hogy nem lehet mindegyik hegyes, hiszen összegük 360 fok. A legnagyobb szög tehát derékszög vagy tompaszög, s ez egy a pontjainkból alakított derékszögű vagy tompaszögű háromszög szöge.
|
|
|
|
| [2293] sakkmath | 2023-04-27 15:48:51 |
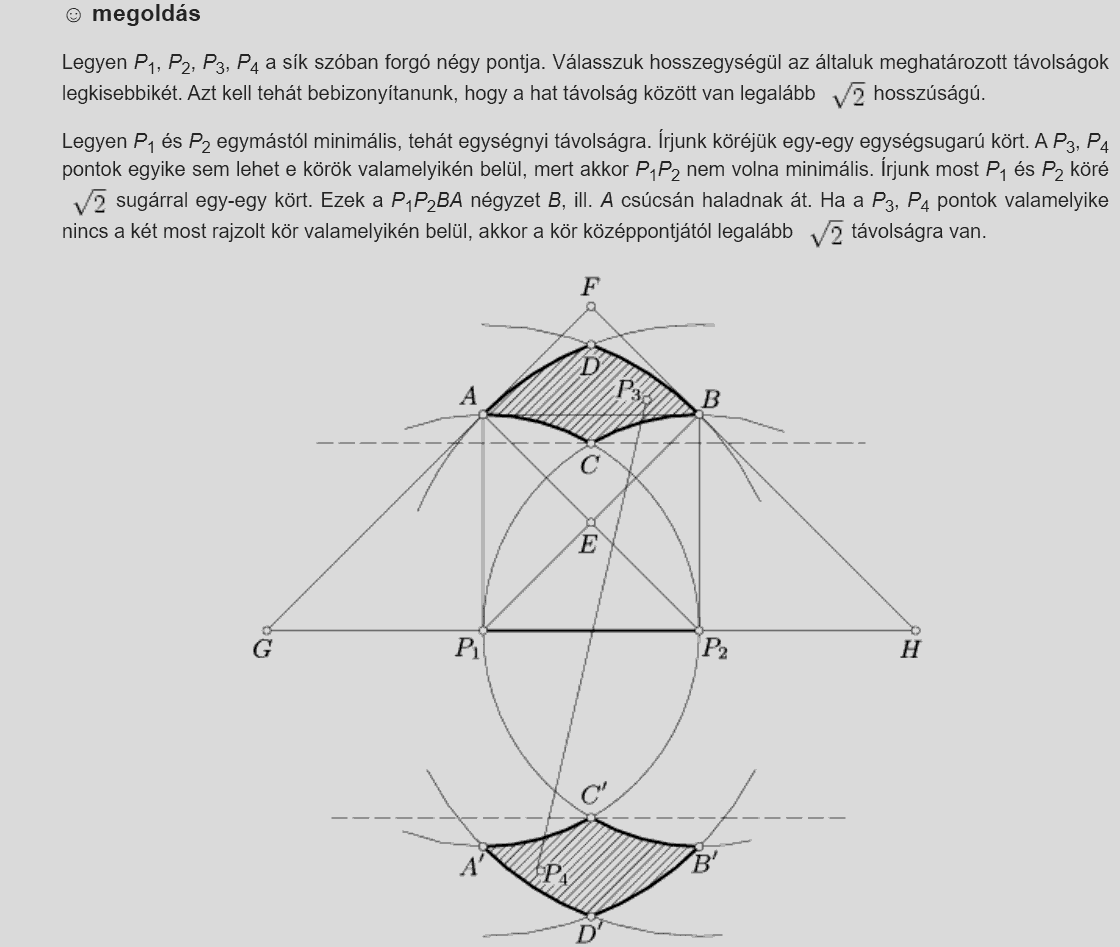
 A bolyai.hu honlapról könnyű eljutni a [Kürschák József Matematikai Tanulóverseny 1961 1. kateg. 1. ford. 9-13. évfolyam] mappáig. Innen másolom be két részletben Hajós György (!) 1. feladatra adott megoldását. E feladat eredeti kitűzési szövege:
A sík négy pontja hat távolságot határoz meg. Bizonyítsuk be, hogy e távolságok legnagyobbika a legkisebbel osztva nem adhat \(\displaystyle \sqrt2\) -nél kisebb hányadost.
A megoldás első része:
|
 |
| Előzmény: [2292] marcius8, 2023-04-26 21:17:36 |
|
| [2292] marcius8 | 2023-04-26 21:17:36 |
 Megint találkoztam egy feladattal: Bizonyítandó, hogy a síkon bárhogy is választunk ki négy pontot, a köztük előforduló hat távlság maximumának és minimumának hányadosa legalább \(\displaystyle 2^{1/2}\). Inkább arról van szó, hogy hogyan kell szépen és egyszerűen bizonyítani, mert körülményesen össze tudom hozni a bizonyítást. Minden segítséget előre is köszönök.
|
|
|
| [2290] nadorp | 2023-02-17 16:59:29 |
 Elnézést kérek, de az előző hozzászólásban alábbi mondat nem igaz:
Az még elmondható, hogy \(\displaystyle b_n\) egy felső korlátja a mértani sor - bár már ehhez is hozzá kéne tenni , hogy ez a fenti limesz monotonitása miatt van
A \(\displaystyle b_{n,k}\) sorozat ui. csak elég nagy n-re kisebb a határértéknél, de ez nem nyilvánvaló állítás. Ezért is szerencsésebb a megoldásban tekintett másik sorozat, \(\displaystyle a_{n,k}\) vizsgálata, mert az monoton nő.
|
| Előzmény: [2289] nadorp, 2023-02-17 14:37:55 |
|
| [2289] nadorp | 2023-02-17 14:37:55 |
 Az alábbi rész kérdőjeles:
\(\displaystyle \lim_{n\to\infty}\Bigg(\frac{n}{n+1}\Bigg)^n+\Bigg(\frac{n-1}{n+1}\Bigg)^n+\Bigg(\frac{n-2}{n+1}\Bigg)^n+\Bigg(\frac{n-3}{n+1}\Bigg)^n+\dots ?= e^{-1}+e^{-2}+e^{-3}+e^{-4}+\dots\)
Ha \(\displaystyle b_n=\Bigg(\frac{n}{n+1}\Bigg)^n+\Bigg(\frac{n-1}{n+1}\Bigg)^n+\dots+ \Bigg(\frac{1}{n+1}\Bigg)^n\)
akkor attól még, hogy a tagok "függőlegesen" konvergálnak, tehát hogy fix k-ra
\(\displaystyle \lim_{n\to\infty}\Bigg(\frac{n-k}{n+1}\Bigg)^n=e^{-k-1}\)
még nem következik, hogy az \(\displaystyle e^{-k-1}\) határértékek összege megegyezik \(\displaystyle b_n\) határértékével. Az még elmondható, hogy \(\displaystyle b_n\) egy felső korlátja a mértani sor - bár már ehhez is hozzá kéne tenni , hogy ez a fenti limesz monotonitása miatt van - de hogy oda konvergál-e, az nem következik az általad leírtakból.
Ha \(\displaystyle b_{n,k}=\Bigg(\frac{n-k}{n+1}\Bigg)^n\) ha \(\displaystyle 0\leq k \leq n\) és \(\displaystyle b_{n,k}=0\) ha \(\displaystyle k>n\), akkor azt állítod, hogy
\(\displaystyle \lim_{n\to\infty}\sum_{k=0}^nb_{n,k}=\lim_{n\to\infty}\sum_{k=0}^\infty b_{n,k}=\sum_{k=0}^\infty(\lim_{n\to\infty}b_{n,k})\)
Viszont a fenti határátmenet csere nem nyilvánvaló.
A "szabályos" eljárás az, ami sakkmath 2. megoldásában van (Tannery-tétel). A képletek (indexek) egyszerűbbek lesznek, ha sakkmath megoldását követve a \(\displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}\left(\frac{k}{n}\right)^n=\lim_{n\to\infty}S_n\) határértékét számoljuk először ki, aztán osztjuk e-vel.
Minden \(\displaystyle n\geq1\) esetén legyen:
\(\displaystyle a_{n,k}=\Bigg\{\begin{matrix}\bigg(\frac{n-k}{n}\bigg)^n & 0\leq k\leq n \\ 0 & k> n \\ \end{matrix}\).
Ez egy végtelen mátrix, aminek a főátlójában - kivéve az \(\displaystyle a_{1,0}\) -és felette minden elem 0, a nulladik (azaz az első) oszlop csupa 1-es.
Bármely fix k-ra ismert, hogy az \(\displaystyle a_{n,k}\) sorozat monoton növekvő és határértékére
\(\displaystyle \lim_{n\to\infty}a_{n,k}=e^{-k} \tag{1}\)
Legyen \(\displaystyle \varepsilon>0\) rögzített. Mivel \(\displaystyle \sum_{k=0}^{\infty}e^{-k}=\frac{e}{e-1}=S\), ezért létezik K, hogy
\(\displaystyle \sum_{k=0}^{K}e^{-k}>S-\varepsilon \tag{2}\)
Másrészt (1)-ben a monotonitás miatt
létezik \(\displaystyle N_0\), hogy \(\displaystyle n>N_0\) esetén \(\displaystyle 1-a_{n,0}<\frac\varepsilon {K+1}\)
létezik \(\displaystyle N_1\), hogy \(\displaystyle n>N_1\) esetén \(\displaystyle \frac1{e}-a_{n,1}<\frac\varepsilon {K+1}\)
...
létezik \(\displaystyle N_K\), hogy \(\displaystyle n>N_K\) esetén \(\displaystyle \frac1{e^K}-a_{n,K}<\frac\varepsilon {K+1}\)
Így, ha \(\displaystyle N:=\max(K,N_0,...,N_K)\), akkor összeadva a fenti K+1 darab egyenlőtlenséget, \(\displaystyle n>N\) esetén teljesül
\(\displaystyle \sum_{k=0}^{K}e^{-k}-\sum_{k=0}^{K}a_{n,k}<\varepsilon\)
Felhasználva (2)-t is:
\(\displaystyle \varepsilon>\sum_{k=0}^{K}e^{-k}-\sum_{k=0}^{K}a_{n,k}>
S-\varepsilon-\left(\sum_{k=0}^{n}a_{n,k}-\sum_{k=K+1}^{n}a_{n,k}\right)>S-\varepsilon-\sum_{k=0}^{n}a_{n,k}=S-S_n-\varepsilon\)
Azaz \(\displaystyle S-S_n<2\varepsilon\)
|
| Előzmény: [2288] marcius8, 2023-02-16 22:28:25 |
|
| [2288] marcius8 | 2023-02-16 22:28:25 |
 Nekem így lett meg a határérték. Mondjuk nem túl precíz.....
\(\displaystyle \lim_{n\to\infty}\frac{1^n+2^n+3^n+\dots"
+(n-2)^n+(n-1)^n+n^n}{(n+1)^n}=\)
\(\displaystyle \lim_{n\to\infty}\frac{n^n+(n-1)^n+(n-2)^n+(n-3)^n+\dots"
+3^n+2^n+1^n}{(n+1)^n}=\)
\(\displaystyle \lim_{n\to\infty}\Bigg(\Bigg(\frac{n}{n+1}\Bigg)^n+\Bigg(\frac{n-1}{n+1}\Bigg)^n+\Bigg(\frac{n-2}{n+1}\Bigg)^n+\Bigg(\frac{n-3}{n+1}\Bigg)^n+\dots\Bigg)=\)
\(\displaystyle e^{-1}+e^{-2}+e^{-3}+e^{-4}+\dots\)=végtelen mértani sor=
\(\displaystyle \frac{e^{-1}}{1-e^{-1}}\)=\(\displaystyle \frac{1}{e-1}\)
Menet közben felhasználtam a következő határértéket:
\(\displaystyle \lim_{n\to\infty}\Bigg(\Bigg(\frac{n+a}{n+b}\Bigg)^n\Bigg)=e^{a-b}\)
|
|
| [2287] marcius8 | 2023-02-16 21:59:33 |
 Először is köszönöm Johnny 10 és Sakkhmath alapvetően segítő jellegű válaszait.
Én csak egy egyszerű határértékre kérdeztem, ami nem volt sürgős, március közepéig ráért. Persze azóta kaptam máshonnan segítséget, Johnny 10 hivatkozott egy Kömal-feladatra. Megnéztem én is az említett feladatot. Ott egy diofantoszi egyenletet kellett megoldani. Ha az egyenletet elosztom a jobb oldallal, akkor a jobb oldalon 1 van, a bal oldalon egy az, általam kérdezett sorozathoz hasonló jellegű sorozat van. Ha erről a hasonló jellegű sorozatról megmutatom, hogy konvergens, van határértréke, azzal még nem oldom meg a diofantoszi egyenletet. Ugyanis bármennyire is konvergens az a hasonló jellegű sorozat, még lehet nagyon sok (nem végtelen) olyan "kiugró" tagja, amelynek értéke mondjuk pl 1. Hogy tudjam használni a hasonló jellegű sorozat konvergenciáját, ahhoz az kell, hogy minden \(\displaystyle \epsilon>0\) értékhez találjak egy \(\displaystyle n\) értéket, ahonnan kezdve a sorozat minden tagjának a határértéktől vett eltérése \(\displaystyle \epsilon\)-nál kisebb legyen. Ez viszont egy újabb feladat, amit most nagy hirtelen nem tudnék megcsinálni. Akkor már jobb, ha azt mutatom meg a hasonló jellegű sorozatról, hogy szigorúan monoton csökkenő.
Mindenfajta személyeskedést elkerülve nem volt szándékom az említett versenyfeladat megoldására vagy annak egy részére rákérdezni, ezúton is bocsánatot kérek a szerkesztőségtől, a versenyzőktől és a versenybizottságtól. Tisztelettel: BZ.
|
| Előzmény: [2282] Johnny 10, 2023-02-14 19:17:19 |
|
| [2286] sakkmath | 2023-02-16 00:01:05 |
 Lemma:
Az \(\displaystyle {\Large a_n}=\frac{\large 1^n+2^n+3^n+...+n^n}{\large n^n}\), n=1, 2, 3, … sorozat határértéke: \(\displaystyle \Large \lim_{n\to\infty}{\Large a_n}=\frac{\large e}{\large {e-1}}\).
A lemma első bizonyítása itt, a 2. pedig emitt található. (Az utóbbi webhelyen a Tannery-tételt és több alkalmazását tanulmányozhatjuk.)
Jelöljük \(\displaystyle {\Large b_n}\)-nel a \(\displaystyle {\large \bf [2275]}\)-ben megadott sorozat \(\displaystyle {\large n}\)-edik tagját; \(\displaystyle {\large n= 1, 2, 3, …}\)
Ekkor
|
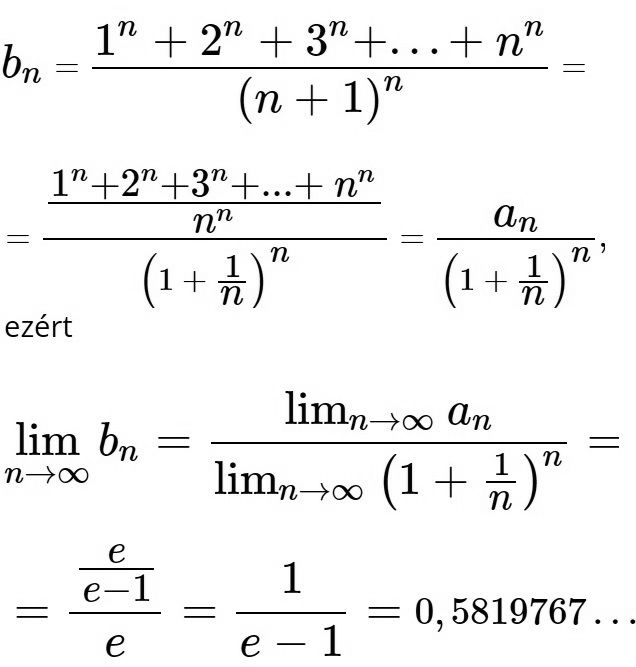 |
| Előzmény: [2275] marcius8, 2023-02-01 16:30:17 |
|
| [2285] Johnny 10 | 2023-02-15 16:49:23 |
 Akkor föloldom :) (Egyébként az előző hsz.e-mben elég hülyeség az egyenlet, ha valaki nézte (persze ez csak egy morzsája volt amúgy is a feladat megoldásának), valójában eredetileg természetesen a \(\displaystyle \bigg(\frac{3}{n+3}\bigg)^n+\bigg(\frac{4}{n+3}\bigg)^n+...+\bigg(\frac{n+2}{n+3}\bigg)^n\) kifejezést kell felülről becsülni, és ehelyett kell a csel.)
|
|
|
|
| [2282] Johnny 10 | 2023-02-14 19:17:19 |
 Még azzal tartozom, hogy leírjam, miért nem akartam, hogy valaki korábban feltegyen rá megoldást. A válasz egyszerű: a múlt hónapban lejárt B.5290. feladat. Ugyanis a határértékes feladatból elég sok mindent ki lehet találni a bizonyításhoz, igaz persze még így is nagy ötlet az általam ismert ilyen megoldásban (sajátom), hogy nem \(\displaystyle \bigg(\frac{3}{n}\bigg)^n+\bigg(\frac{4}{n}\bigg)+...+\bigg(\frac{n+3}{n}\bigg)^n\)-t kell felülről becsülni, hanem \(\displaystyle \bigg(\frac{1}{n}\bigg)^n+\bigg(\frac{2}{n}\bigg)^n+...+\bigg(\frac{n-1}{n}\bigg)^n,\) és utána a maradék tagokra egy újabb felső becslést kell bevetni, de egy ilyen megoldás megtalálásában sokat segíthetne ennek a felvetett kérdés megoldása. Mivel azonban nem akartam túl egyértelműen utalni arra, hogy ez releváns info a feladathoz, ezért lett belőle ez a talányos hozzászólás. (Az viszont érdekes, hogy én ezt úgy írtam, hogy biztos voltam benne, hogy aki követi a KöMaL-t, annak egyértelmű, hogy miért írtam a hozzászólást, mert nem hittem, hogy létezik az én megoldásomon kívül másfajta megközelítés. Pedig a hivatalos megoldást elnézve teljes indukció is elég, így valószínűleg senkinek nem esett le...)
|
| Előzmény: [2279] marcius8, 2023-02-02 08:25:07 |
|