| [253] epsilon | 2007-12-04 18:15:45 |
 Helló! Köszi, nem ez, lehet, hogy nem voltam elég világos az alábbi egyenletrendszerről van szó, teljesen elemi módon, mikor hány megoldás van:
|
 |
|
|
| [251] epsilon | 2007-12-04 12:08:09 |
 Tisztelt Fórumtagok! megint Én jelentkezem kérdéssel, régóta nézelődöm ezen a téren, de segítségre lenne szükségem: Tudna-e Valaki mondani neten elérhető forrásanyagot (magyar, angol vagy francia, de más latin nyelvcsaládban sem rossz) arról, hogy miként lehet megoldani modulo n-ben 2 ismeretlenes 2 egyenletből álló egyenletrendszert. Mert van amikor megy a kifejezési módszerrel, van amikor megy a kiküszöüblés módszer, van amikor megy a Cramer-szabálal, de van amikor csak "okoskodással" lehet megoldani. A megoldhatósági feltételek, esetek rendszerezését szeretném tudni, hogy miként lehet tárgyalni. Ugyanakkor érdekelne mindez 3 ismeretlenes, 3 egyenletből álló modulo n egyenletrendszerre is, természetesen mindenesetben csak lineáris egyenletrendszerre gondoltam Bárminemű segítséget előre is köszönök! Üdvözlettel: epsilon
|
|
| [250] epsilon | 2007-11-25 10:24:55 |
 Kedves Lajos! Köszi szépen, mert azt hittem, tévúton járok, ugyanis mielőtt ide kiírtam volna a feladatot, azelőtt az [f(y)-f(x)]/(y-x) arányt vizsgálva, pontosan idáig jutottam el mint amit Te írsz (persze y-x nélkül), és azt hittem, hogy zsákutca. De mivel Te is ezt követted, innen kihámoztam, hogy végűl keresztbe szorozva, TAGPÁRONKÉNT összehasonlítva elegendő ha x és y-ra teljesüljön ilyen feltétel: a-t>=t-b ami éppen a szóban forgó intervallumba való tartozást jelenti. Üdv: epsilon
|
|
|
| [248] epsilon | 2007-11-24 15:54:37 |
 Helló! Valaki tudna-e segíteni abban, hogy a következő feladatot NE a matematikai analízis módszerével oldja meg! Előre is köszönöm a segítséget!
|
 |
|
| [247] Bubóka | 2007-11-02 13:08:11 |
 Üdv Mindenkinek!
Segítséget szeretnék kérni a következő feladathoz. Aki esetleg tud, megköszönném!!
Bizonyítsuk be, hogy az alábbi háromszögszerkesztési feladatok nem szerkeszthetők euklidészi értelemben! A harmadfokú problémáknál vizsgáljuk, hogy megoldható-e szögharmadoló eszközzel.
1. (a, ha, wb ) = ( p/2, 1, 2 )
2. (a, ha, wb ) = ( 1, 1, 1 )
Nem tudom mennyire egyezményesek ezek a jelek, a w - a szögfelezőt, h- a magasságot jelentené.
|
|
| [246] Róbert Gida | 2007-11-01 23:16:08 |
 Nem. Csak megnéztem néhány speciális esetet és be is tudtam bizonyítani. Ezek szerint, ha p=4*k+1 alakú prím, akkor
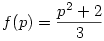
, ahol f(p) az a feladatban definiált összeg. Kis számelmélet kell hozzá.
|
| Előzmény: [245] jonas, 2007-11-01 22:47:51 |
|
|
|
| [243] jonas | 2007-11-01 21:27:22 |
 Az ilyenre a standard procedúra a következő. Kiszámolod kis n-ekre. Nekem ez jött ki:
0,1,2,4,7,9,13,18,24,29,34,42,51,57,67,78,90,97,110,122,137,149,163,180,198,211,226,246,265,281
Ezt megkeresed a Sloane-ben (vesszővel elválasztva kell beírni).
Az eredményekből kiválasztod a megfelelő sorozatot, és megsejted, hogy az az eredmény. Utána bebizonyítod.
Ebben az esetben elég sok tagunk van, hogy csak egy sorozatot találjunk: A014817, és annak a definíciója nagyon hasonlít a képletedhez (csak még a 0-t is hozzáveszi).
Sajnos explicit képletet nem ad. Ezért azt lehet sejteni, hogy vagy nincs explicit képlet, vagy nehéz megtalálni.
|
| Előzmény: [242] SÁkos, 2007-11-01 18:39:08 |
|
|
| [241] SÁkos | 2007-11-01 18:11:32 |
 Üdv mindenkinek!
A következőt szeretném kérdezni:
Létezik explicit alakja 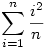 -nek? és ha igen, mi az? -nek? és ha igen, mi az?
|
|
| [240] Daniel | 2007-10-30 22:49:37 |
 Sziasztok! Az lenne a kérdésem, hogy a KöMaL CD-n található 1735-ös feladat megoldásában (1972. október, 72. oldal) mit jelent a Ptolemaiosz-Dürer-féle eljárás?
|
|
|
| [238] arnoldino | 2007-10-23 22:26:36 |
 udv mindenkinek
van valaki aki tudna nekem segiteni dualis kvaterniokkal kapcsolatban?
|
|
| [237] Lengyel_Ferenc1 | 2007-10-14 10:48:48 |
 Üdvözletem!
Eszembe jutott egy feladat az úgynevezett Levi-sejtés kapcsán, és az 5-ös szám vizsgálata közben. A Levi-sejtés azt mondja ki, hogy minden páratlan szám felosztható olyan három prímszámra, amelyek közül kettő egyenlő, egy pedig nagyobb a másik kettőnél. Vegyük azokat a prímeket, amelyeknek, ha a páros felét elosztjuk kettővel szintén prímet kapunk. Ilyen számok például:
(7 = 3+4) (4/2 = 2), (11 = 5+6) (6/2 = 3)
Most adjuk hozzá ezekhez a számokhoz saját páros felüket.
7+4 = 11, 11+6 = 17
Láthatjuk, hogy szintén prímeket kaptunk. Ilyen prímek még a 19, 29 vagy a 43 is. Vagyis olyan prímek, amelyeknél van olyan kisebb prím, amelyiknek ha a páros felét elosztjuk kettővel szintén prímet kapunk, és ha ezt a páros felet hozzáadjuk saját magához, akkor megkapjuk ezeket a prímeket. A feladat tehát az lenne, hogy bizonyítsuk be: végtelen sok ilyen prím van. Én sajnos nem tudom bebizonyítani. Ha az interneten megvan valahol a bizonyítás és megmutatnátok annak is örülnék. Segítséget előre is köszönöm.
|
|
| [236] Daisy | 2007-10-13 16:11:27 |
 Nagyon köszönöm a segítséget :) A feladat az volt, hogy azt kellett "bebizonyítani" hogy az égés oxigént használ, és ha az oxigén elfogy, azt ki kell valaminek töltenie. Véletlenül 13:2-t írtam, de a lapon jó volt, csak már fáradt voltam.
|
| Előzmény: [235] SmallPotato, 2007-10-12 14:44:59 |
|
| [235] SmallPotato | 2007-10-12 14:44:59 |
 "Nincsenek ovis kísérletek, csak érdeklődő emberek vannak." (idézet tőlem :-) )
Szóval szerintem lehet jó ... de alapvetően az lenne a kérdés(em), hogy mi volt a feladat? "Eredményt" kaptál, írod. Minek az eredményét?
Ha a gyertya ég, ehhez oxigént használ el (ezzel az üvegben a gáz nyomását csökkenti), és valamiféle (főként gáznemű) égésterméket állít elő (ezzel a gáz nyomását növeli). Emellett a láng csökkenésével, majd kialvásával az üveg alatti gázkeverék hőmérséklete csökken, ez a gáz nyomását megint csak csökkenti.
A három folyamat eredőjeként az üveg alatt a nyomás végülis csökkenni fog; ezért a külső légnyomás valamennyi vizet benyom az egyensúlyt tartani nem képes belső nyomással szemben. A benyomott víz"oszlop" magasságából (és nem a térfogatarányból) származó hidrosztatikai nyomás lesz az, ami a nyomáskülönbséggel egyensúlyt tart. Ilyenformán a 13/2 (inkább 2/13-ot mondanék) mint arány lehet jó is, de szerintem szinte semmire sem válasz.
|
| Előzmény: [234] Daisy, 2007-10-11 20:19:12 |
|
| [234] Daisy | 2007-10-11 20:19:12 |
 Sziasztok! Van egy kérdésem, hogy jól okoskodtam-e a (Nektek biztosan) ovis kísérletemben. 7.-es vagyok... Vízben (parafadugóra) gyertyát tettem és meggyújtottam. Befőttesüveget tettem rá, és amikor elaludt a gyertya, a levegő helyére bement a víz. Az eredményt úgy kaptam, hogy a vízszint növekedést elosztottam az üveg teljes magasságával. Igy 13:2 arány jött ki. EZ LEHET JÓ???? Előre is köszönöm.
|
|
| [233] jonas | 2007-07-26 19:36:17 |
 Nekem ezek nem tűnnek valami meglepőnek.
Nézzük először azt, milyen (pozitív) páratlan számnak lehet a fele körül a prímosztóinak az összege. Egy nagy prímszámnak nyilván nem. Magy összetett páratlan számnak pedig minden prímosztója legalább 3, ezért minden prímosztó legfeljebb az egy harmada a számnak, ezért ha ezeknek az összege majdnem feleannyi, mint maga a szám, akkor a szám prímosztóinak száma majdnem egy hatoda a számnak, ami nagy számoknál nyilván abszurd. Kis számoknál számítógéppel könnyen ellenőrizhető, hogy csak az 1, a 15 és a 21 teljesíti a feltételt. (Hasonló igaz egyébként a páros számokra is, ezek közül csak a 4-nek és a 12-nek a fele egyenlő a prímosztóinak összegének.)
Teljesen hasonló a helyzet, amikor olyan (pozitív) számot keresünk, aminek a fele egyenlő (legfeljebb 1/2 eltéréssel) a számjegyeinek összegével: egy nagy szám sokszor nagyobb, mint a számjegyeinek összege, ezért csak a 0, 1, 17, 18, 19 megoldások.
A számjegyek szorzata már egy kicsit nehezebb kérdés, mert nem lehet olyan élesen becsülni. Egy n jegyű szám számjegyeinek a szorzata legfeljebb m.9n-1, ha m az első számjegy, a szám maga pedig legalább m.10n-1, tehát csak akkor zárhatjuk ki az egyenlőséget, ha 1+2m.9n-1<10n-1m, ami igaz, ha 2<(10/9)n-1, ami pedig 7<n esetén teljesül. Tehát csak 107-ig kell ellenőrizni a számokat, ami szerencsére még könnyű számítógéppel.
Eredménynek azt kapjuk, hogy csak a következő számoknak van meg ez a tulajdonságuk (ha el nem rontottam valamit): 0 1 19 27 36 289 379.
|
| Előzmény: [232] Lengyel_Ferenc1, 2007-07-25 23:21:13 |
|
| [232] Lengyel_Ferenc1 | 2007-07-25 23:21:13 |
 Üdvözletem!
A kérdésem a 15-ös és a 21-es számokkal lenne kapcsolatos. Minden páratlan számnak van egy nagyobbik fele és egy kisebbik fele. A nagyobbik fele egyel nagyobb, mint a kisebbik fele. Így például: 5 = 3 + 2, 7 = 4 + 3, 9 = 5 + 4 És vannak olyan páratlan számok, amelyeknek prímosztóinak összege egyenlő a kisebbik vagy nagyobbik felükkel. Így például: 15-nek az osztói: 1, 3, 5, 15. Ebből 5 és 3 prímek. 15 pedig 8 + 7-el egyenlő, tehát 8 a nagyobbik fele. És 5 + 3 = 8. 21 osztói: 1, 3, 7, 21. Ebből 3 és 7 prímek. 21 pedig 10 + 11-el egyenlő, tehát 10 a kisebbik fele, és 7 + 3 = 10. Most nézzük meg azokat a számokat, amelyeknek számjegyeiknek összege egyenlő saját kisebbik illetve nagyobbik felükkel. Egy ilyen párt találtam a 17-et és a 19-et. Hiszen 17 számjegyeinek összege: 1+7 = 8. És 8+9 = 17. Vagyis számjegyeinek összege egyenlő a kisebbik felével. 19 számjegyeinek összege: 1+9 = 10. És 10+9 = 19. Vagy számjegyeinek egyenlő a nagyobbik felével. És érdekes módon 17 és 19 pontosan a 15 és a 21 között elhelyezkedő két legközelebbi (a 15-höz és a 21-hez is legközelebbi) szomszédos páratlan szám. És még egy érdekes összefüggés a két számmal kapcsolatban: 1+2+3+4+5+6=21, 1+2+3+4+5=15. Vagyis, ha a természetes számok első 6 tagját egymáshoz adjuk pont 21-et kapunk, ha az első ötöt, akkor pont 15-öt. Vajon minek köszönhető, hogy ennyi összefüggés van a két szám között? A 19 viszont nem csak olyan páratlan szám, amelynek számjegyeinek összege egyenlő saját nagyobbik felével, hanem egyben az első olyan páratlan szám is egyben, amelynek számjegyeinek szorzata egyenlő saját kisebbik felével, hiszen 1 * 9 = 9 és 19 = 10 + 9. Az első olyan páratlan szám, amelynek számjegyeinek szorzata egyenlő saját nagyobbik felével viszont nem más, mint a 27. Hiszen 2 * 7 = 14 és 14 + 13 = 27. Az lenne a kérdésem tehát, hogy mi az oka a 15-ös és a 21-es szám ezen érdekes tulajdonságainak és, hogy tud e valaki még ilyen számpárokról.
|
|
|
|
|





 x
x