| [299] epsilon | 2008-03-01 19:03:57 |
 Sziasztok! Egy harmadik feladat ([a] az a szám egészrésze):
|
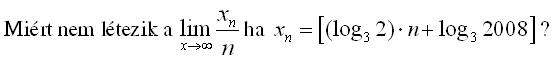 |
|
| [298] epsilon | 2008-03-01 18:58:05 |
 Sziasztok! Egy második szép feladat:
|
 |
|
| [297] epsilon | 2008-03-01 18:48:18 |
 Sziasztok! Megint jelentkezem egy számomra nem egyértelmű feladattal. A következő feladatban azon "a" paraméterek számát kérdik, amelyekre az f(x) függvény konvex a [0,1]-en. A válasz az, hogy 2 ilyen érték van, Én meg vagy 1-et, vagy 0-át találok, aszerint, hogy azt vizsgálom, hogy a függvény folytonos kell legyen, meg a deriváltja is.Nektek mi a véleményetek? Előre is kösz! Üdv: epsilon
|
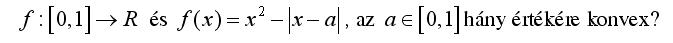 |
|
| [296] Sirpi | 2008-02-19 20:52:46 |
 Na, kigyötörtem. És amilyen egyszerű, olyan sokáig tartott. Az a (teljes indukciós) állítás, hogy n ember esetén mindig ki lehet megfelelően n-1 kérdést választani, hogy ezen a részhalmazon mindenki különböző választ adjon.
Kezdőlépés: n=1: nem kell kiválasztani egyik kérdést sem
n=2: Ilyenkor nyilván van olyan kérdés, aminél eltér a válasz, válasszuk azt.
Indukciós lépés (n n+1): válasszunk egy olyan kérdést, amire nem adta mindenki ugyanazt a választ (ilyen van, különben mindenkinek minden kérdésre azonos választ kellett adnia, ami lehetetlen). A válaszok szerint bontsuk csoportokra az embereket - az azonos választ adók kerülnek egy csoportba. Nem kell feltenni, hogy csak kétféle (pl. igen-nem) válasz adható. Az előző megjegyzés szerint legalább két csoport lesz. Álljanak a csoportok a1,a2,...,ak emberből. A csoportokra alkalmazzuk az indukciós feltevést, és ilyenkor (létszám-1) tesztkérdés kiválasztható az adott csoporthoz, ezeket összeadva kijön, hogy összességében elég 1+(a1-1)+...+(ak-1) tesztkérdés, ami k n+1): válasszunk egy olyan kérdést, amire nem adta mindenki ugyanazt a választ (ilyen van, különben mindenkinek minden kérdésre azonos választ kellett adnia, ami lehetetlen). A válaszok szerint bontsuk csoportokra az embereket - az azonos választ adók kerülnek egy csoportba. Nem kell feltenni, hogy csak kétféle (pl. igen-nem) válasz adható. Az előző megjegyzés szerint legalább két csoport lesz. Álljanak a csoportok a1,a2,...,ak emberből. A csoportokra alkalmazzuk az indukciós feltevést, és ilyenkor (létszám-1) tesztkérdés kiválasztható az adott csoporthoz, ezeket összeadva kijön, hogy összességében elég 1+(a1-1)+...+(ak-1) tesztkérdés, ami k 2 miatt legfeljebb n-1. Ha legalább 3 csoport van, akkor ennél kevesebb is elég. 2 miatt legfeljebb n-1. Ha legalább 3 csoport van, akkor ennél kevesebb is elég.
----
Van olyan elrendezés, amihez kell is ennyi kérdés, pl. ha a k. ember csak a k. kérdést rontja el. Ilyenkor az első 20 kérdésből muszáj 19-et kiválasztanunk, hogy azok alapján különbözzenek a tanulók.
(Bocs, ha nem teljesen érthető minden, kicsit gyorsan írtam.)
|
| Előzmény: [295] komalboy, 2008-02-18 16:38:17 |
|
| [295] komalboy | 2008-02-18 16:38:17 |
 Egy kis verseny-feladat... : Egy vállalat a hozzá jelentkezőket egy 25 pontból álló teszttel vizsgálja. A legfrissebben meghiretett állásra 20 fő jelentkezett, kinek a teszteredményei mind különbözőek, semelyik kettő sem azonos teljesen. Mutassuk meg, hogy kiválasztható 19 tesztkérdés úgy, hogy a 20 teszt közül bármely kettő között lesz eltérés ezen 19 kérdés alapján is.
|
|
|
|
| [292] Sirpi | 2008-02-15 11:50:48 |
 Kicsit kavar van itt... Egyrészt "a két átlóval bezárt szög" helyett nem azt akartad írni, hogy "a két átló bezárt szöge"? Mert ha a két átló bezárt szöge 60o, akkor a koszinusztételből és abból, hogy az átlók felezik egymást, következik, hogy:
a2=(e/2)2+(f/2)2-2.e/2.f/2.cos 60o
b2=(e/2)2+(f/2)2-2.e/2.f/2.cos 120o
Vagyis:
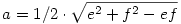
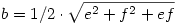
Amúgy pedig a köv. hozzászólásban említett "átlók négyetösszege egyenlő az oldalak négyzetösszegével" helyesen úgy hangzik, hogy e2+f2=2a2+2b2
|
| Előzmény: [290] gele_viki, 2008-02-14 20:15:54 |
|
| [291] nehajolehet | 2008-02-15 11:07:32 |
 Paralelogrammánál az átlók hosszának négyzetösszege megegyezik az oldalak hosszának négyzetösszegével. Tehát e=sin"alfa", f=cosß, a=sin2"alfa", a=?, b=? kérdésre a válasz: e ad 2 + f ad 2 = a ad 2 + b ad 2, ezután a többi csak számolás. Szerintem.
|
| Előzmény: [290] gele_viki, 2008-02-14 20:15:54 |
|
| [290] gele_viki | 2008-02-14 20:15:54 |
 tudna nekem segíteni valaki?
Van egy paralelogramma, aminek a hosszabbik átlója ,f', a rövidebbik ,e'. A két átlóval bezárt szög 60 fok. e=sin"alfa", f=cosß, a=sin2"alfa", a=?, b=? Bocsi az alfáért de nem tudom hol van a billentyűn :) Előre is köszönöm!
|
|
|
| [288] nadorp | 2008-02-14 17:12:39 |
 Ha x2+ax+b=y2, akkor
4x2+4ax+a2+4b=4y2+a2
(2x+a)2-4y2=a2-4b
(2x+a-2y)(2x+a+2y)=a2-4b
Ha a2-4b 0, akkor csak véges sok két tényezős felbontása létezik, tehát az eredeti kifejezés nem lenne végtelen sok x helyen négyzetszám. Tehát a2-4b=0, azaz 0, akkor csak véges sok két tényezős felbontása létezik, tehát az eredeti kifejezés nem lenne végtelen sok x helyen négyzetszám. Tehát a2-4b=0, azaz
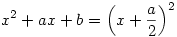
|
| Előzmény: [286] Pardeller, 2008-02-13 18:54:43 |
|
| [287] nemtommegoldani | 2008-02-13 21:38:49 |
 Kedves Python! Nagyon köszönöm a segítséget, és a nagyon gyors választ!
|
|
| [286] Pardeller | 2008-02-13 18:54:43 |
 Tegyük fel, hogy x2+ax+b végtelen sok egész x-re négyzetszám (a és b is egész). Bizonyítsuk be, hogy ekkor a kifejezés egy elsőfokú polinom négyzete. Matek szakkör, Pell-féle egyenletek volt a témakör, de más természetű megoldásokat is szívesen fogadok :) Előre is köszönöm.
|
|
| [285] Python | 2008-02-13 18:43:38 |
 25.34.73.1111 pozitív osztóinak a száma az ismert képlet alapján (5+1)(4+1)(3+1)(11+1). (prímkitevő+1 alakú tényezők szorzata minden prímre a prímfelbontásból; ha a szám egy p prímnek az a-adik hatványával osztható, a+1-edikkel nem, akkor p kitevője a+1 féle (0, 1, 2, ..., a) lehet egy osztójában.)
|
| Előzmény: [283] nemtommegoldani, 2008-02-13 18:35:00 |
|
|
| [283] nemtommegoldani | 2008-02-13 18:35:00 |
 Az előbbi hozzászólásomhoz még egy feladatot elfelejtettem: Határozd meg a 2 az ötödiken*3a negyediken*7 a harmadikon*11 a tizenegyediken pozitív osztóinak számát! Köszönöm szépen!
|
|
| [282] nemtommegoldani | 2008-02-13 18:15:16 |
 Újabb feladattal bombázok! Mutassa meg, hogy minden n term. szám esetén az n négyzet+3n+3 és n+1 relatív prímek! Ismét csak köszönetet tudok mondani annak a kedves embernek, aki ezt megfejti nekem.
|
|
| [281] nadorp | 2008-02-11 22:26:25 |
 Természetesen igazad van, de a célom pont az volt, amit Rizsesz leírt, ti. az ax+by=c diofantikus egyenletet pont így oldjuk meg euklideszi algoritmussal. Én csak egyszerűen behelyettesítettem az általános képletekbe a konkrét értékeket. Szerintem a példát pont azért adták fel, hogy numerikusan is megértsék a bizonyítást, ezért volt az én levezetésem annyira "szájbarágós".
|
| Előzmény: [279] BohnerGéza, 2008-02-11 16:50:13 |
|
| [280] rizsesz | 2008-02-11 16:58:27 |
 Itt pont az volt a lényeg, hogy az általános módszert végigvezessük ezen a konkrét eseten, ami akkor is működik, ha az ax+by=c egyenletben a és b relatív prímek. Itt egy olyan esettel álltunk szemben, ahol nem voltak azok, de maga a módszer természetesen ilyenkor is működőképes.
Ha az ember csak meg akarja oldani, és látja, hogy egyszerű, akkor persze fejben kitalálja a megoldást.
|
| Előzmény: [279] BohnerGéza, 2008-02-11 16:50:13 |
|
|
| [278] nadorp | 2008-02-11 13:18:54 |
 98=77.1+21
77=21.3+14
21=14.1+7
14=7.2+0
Innen a lnko=7.
Az első egyeneletből
21=98-77.1
A második egyeneletből felhasználva az elsőt
14=77-21.3=77-(98-77.1).3=77.4-98.3.
Tehát egy megoldás az x=-3 y=-4, azaz az általános megoldás
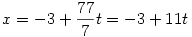
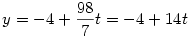
|
| Előzmény: [277] nemtommegoldani, 2008-02-10 22:43:59 |
|
| [277] nemtommegoldani | 2008-02-10 22:43:59 |
 Oldjuk meg a következő diofantikus egyenletet:98x-77y=14 a megadott módon: euklideszi algoritmussal adja meg lnko-t, majd ennek a segítségével adja meg az összes megoldást! A feladatot már megoldottam más módszerrel, de az euklideszi algor. segítségével nem uazt az eredményt kaptam, mint a másiknál. Az jó megoldás, de nem fogadják el, mert az euklideszi algoritmust kellene hozzá használni. Mit téveszthettem az euklideszi algoritmusnál? Köszönöm a választ.
|
|
|
| [275] epsilon | 2008-01-17 06:50:31 |
 Igen, olvasom, az valóban az, de ami a [264] nadorp hozzászólás első felében van, az nem pont az, csak annak a segítségével (olyan típusú egyenlőtlenségek összegezésével) bizonyítják a Cebisev egyenlőtlenséget.
|
|




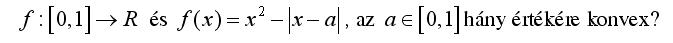

 n+1): válasszunk egy olyan kérdést, amire nem adta mindenki ugyanazt a választ (ilyen van, különben mindenkinek minden kérdésre azonos választ kellett adnia, ami lehetetlen). A válaszok szerint bontsuk csoportokra az embereket - az azonos választ adók kerülnek egy csoportba. Nem kell feltenni, hogy csak kétféle (pl. igen-nem) válasz adható. Az előző megjegyzés szerint legalább két csoport lesz. Álljanak a csoportok a1,a2,...,ak emberből. A csoportokra alkalmazzuk az indukciós feltevést, és ilyenkor (létszám-1) tesztkérdés kiválasztható az adott csoporthoz, ezeket összeadva kijön, hogy összességében elég 1+(a1-1)+...+(ak-1) tesztkérdés, ami k
n+1): válasszunk egy olyan kérdést, amire nem adta mindenki ugyanazt a választ (ilyen van, különben mindenkinek minden kérdésre azonos választ kellett adnia, ami lehetetlen). A válaszok szerint bontsuk csoportokra az embereket - az azonos választ adók kerülnek egy csoportba. Nem kell feltenni, hogy csak kétféle (pl. igen-nem) válasz adható. Az előző megjegyzés szerint legalább két csoport lesz. Álljanak a csoportok a1,a2,...,ak emberből. A csoportokra alkalmazzuk az indukciós feltevést, és ilyenkor (létszám-1) tesztkérdés kiválasztható az adott csoporthoz, ezeket összeadva kijön, hogy összességében elég 1+(a1-1)+...+(ak-1) tesztkérdés, ami k 2 miatt legfeljebb n-1. Ha legalább 3 csoport van, akkor ennél kevesebb is elég.
2 miatt legfeljebb n-1. Ha legalább 3 csoport van, akkor ennél kevesebb is elég. 
 0, akkor csak véges sok két tényezős felbontása létezik, tehát az eredeti kifejezés nem lenne végtelen sok x helyen négyzetszám. Tehát a2-4b=0, azaz
0, akkor csak véges sok két tényezős felbontása létezik, tehát az eredeti kifejezés nem lenne végtelen sok x helyen négyzetszám. Tehát a2-4b=0, azaz 


