|
| [442] S.Ákos | 2008-04-09 21:37:21 |
 Sziasztok!
A B.4055-ös feladatnál (Bizonyítsuk be, hogy minden n!-nál nem nagyobb pozitív egész szám felírható az n! legfeljebb n darab különböző osztójának összegeként.) egész könnyen adódik, hogy n-1 tag is elég n>1 esetén. a kérdés az lenne, hogy ennyi mindig kell-e, vagy ez is csökkenthető tovább, ha n nő, és ha igen, melyik az a függvény, ami megadja a tagok minimális számát?
|
|
| [441] Gyöngyő | 2008-04-09 18:16:40 |
 Sziasztok!
Lenne egy olyan kérdésem,hogy milyen esetben lehet parciális integrálást alkalmazni impropius integrál kiszámitására?
Köszike:
Zsolt
|
|
|
| [438] epsilon | 2008-04-09 15:48:31 |
 Köszi nadorp, mindjárt nem is merek szólni, mert ez valóban átvert, és nem is modhatni kemény diónak, én az x=a×cos2t változócsrét alkalmaztam, és tangenshatványnak az integrálja lett, amit csak rekurziósan bonyolítottam :-(
|
|
|
| [436] epsilon | 2008-04-09 14:25:40 |
 A 434. hsz-ban mindenütt (0,1) helyett [0,1] a helyes. Bocs az elírásért!
|
|
| [435] epsilon | 2008-04-09 14:08:01 |
 Annak örömére, hogy nadorp ilyen szép elemi megoldást adott, fe merészkedek tenni még egy feladatot, szimpatikus, de nem ugrik be :-( Igazolandó, hogy:
|
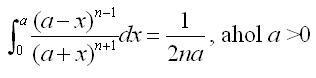 |
|
| [434] epsilon | 2008-04-09 11:01:28 |
 Köszi nadorp! Ez az igazi, amit nem találtam meg. Már-már részletezni akartam, hogy végre elég hosszadalmasan, de megoldottam, de nem tetszik, mert hosszú, noga ötletes. De azért elmesélem: patametrizáltam a [-1,-1/3] intervallumot, ennek parametrizált alakja (2/3)*t-1 ahol t a (0,1) intervallumban van. Tehát f(x) nem egyenlű ezzel az értékkel egyetlen t a (0,1) esetén sem. Ez azt jelenti, hogy a kapott x-ben másodfokú egyenletnek nincsenek valós gyökei, tehát a d<0 (d a diszkrimináns). Ekkor t-ben egy máodfokú egyenlőtlenséget kaptam, nullára rendeztem, és az kell teljesüljön minden t a (0,1) intertvallumból. A baloldali függfényt g(t)-nek jelölve, tehát g(t)<0 minden t a (0,1) intertvallumból. Végül a főegyüttható előjele szerint letárgyalvam mindkét esetben benne kell legyen a g(0)<0 és g(1)<0 feltétel, és a többiekkel is metszve marad ez, ami nem más mint a<-1/4. Kösz szépen mindegyikötöknek az ötletet és a segítséget! Üdv: epsilon
|
| Előzmény: [433] nadorp, 2008-04-09 08:51:32 |
|
| [433] nadorp | 2008-04-09 08:51:32 |
 Az, hogy f(x)<-1 vagy 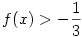 teljesül minden x-re ekvivalens azzal, hogy teljesül minden x-re ekvivalens azzal, hogy  teljesüljön minden x-re. teljesüljön minden x-re.
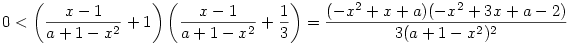
(x2-x-a)(x2-3x-a+2)>0
A baloldal egy pozitív főegyütthatójú negyedfokú polinom,ami pontosan akkor pozitív minden x-re, ha nincs valós gyöke, azaz a szorzatban szereplő másodfokú polinomok diszkriminánsa negatív. Innen 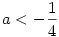
|
| Előzmény: [423] epsilon, 2008-04-07 19:41:32 |
|
| [432] Káli gúla | 2008-04-08 19:27:42 |
 A tört reciproka egyszerűbb függvény, a képe egy hiperbola lesz az y = -x-1 és az x=1 aszimptotákkal. Ha a>0, akkor a tompaszögű tartományban van a függvény és semmilyen értéket nem hagy ki. Ha a<0, akkor az y=-2 egyenesre szimmetrikus sávon kívül halad. Annak, hogy ez a reciprok függvény egy adott k értéket ne vegyen fel, az a feltétele, hogy az 1-x2+a=k(x-1) egyenletnek ne legyen megoldása, azaz a diszkrimináns d=k2+4(k+1+a)=(k+2)2+4a<0 legyen, tehát 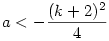 . Ez akár a -1-gyel, akár a -3-mal pont azt adja, amit cauchy írt. Ahogy a-val tartunk a 0-hoz, úgy fog a hiperbola "hegyesedni", és ezért belemetszeni az y=-1 és y=-3 közötti sávba. (A hiperbolára azért érdemes nézni, hogy elhiggyük azt, amit számolunk:) . Ez akár a -1-gyel, akár a -3-mal pont azt adja, amit cauchy írt. Ahogy a-val tartunk a 0-hoz, úgy fog a hiperbola "hegyesedni", és ezért belemetszeni az y=-1 és y=-3 közötti sávba. (A hiperbolára azért érdemes nézni, hogy elhiggyük azt, amit számolunk:)
|
| Előzmény: [431] epsilon, 2008-04-08 17:51:29 |
|
| [431] epsilon | 2008-04-08 17:51:29 |
 Helló! Én úgy próbáltam, hogy ne vegyen fel értékeket a [-1;-1/3] intervallumból, akkor f(x)<-1 vagy f(x)>-1/3 minden x valós szám esetén, aztán egy-egy törtet kaptam, amelyek másodfokú függvényeket tartalmaznak, ás próbáltam a diszkrimináns < 0 feltételeket, a baloldaliból jött ki eredmény, a jobboldaliból nem, de sejtem is a hibát: az f(x)<-1 nem muszáj MINDEN x-re fennáljon, amikor pl. ez nem áll fenn, azon x-re álljon fenn az f(x)>-1/3...tehát nem tudom, hogy a d<0 feltétellel egyáltalán lehetne-e valamit kezdeni. Nézem, a függvány monotonítását, onnan semmi, egyenlővé tettem y-nal és x-ben másodfokú egyenletnek valós megoldásai kell legyene, kaptam y-ra egyenlőtlenséget, vagyis képhalmazt...de ezt sem tudtam összhangba hozni az adott intervallummal..pedig a feladat nem tűnik komolynak, és mégis?!
|
| Előzmény: [430] cauchy, 2008-04-08 15:51:53 |
|
|
|
| [428] epsilon | 2008-04-08 09:10:51 |
 OK Cauchy, ez az eredmény, de Nekem csak az a<0 jön ki, valamit elveszítek :-( Ha a sejtésd bizonyítható, írhatnál egy pár támpontot! Előre is kösz, üdv: epsilon
|
| Előzmény: [424] cauchy, 2008-04-07 21:27:29 |
|
|
| [426] jonas | 2008-04-07 22:55:41 |
 Logaritmust a Taylor-sorral kell számolni, de úgy, hogy előbb leviszed a számot 1 közelébe (lehet fölötte vagy alatta) a log(xy)=logx.logy azonossággal, ahol y-nak ismered a logaritmusát. Ez számítógépnek praktikus, de ha kézzel akarsz logartimust számolni, általában a táblázat egyszerűbb.
|
| Előzmény: [425] leni536, 2008-04-07 22:22:31 |
|
| [425] leni536 | 2008-04-07 22:22:31 |
 A gyökvonásra való módszer nagyon tetszik, már el is sajátítottam a "digit by digit"-et. Más függvényekre van módszer a Taylor-soron kívül? Raj lenne papíron logaritmust számolni. Amúgy ha egy fügvénynek könnyebben számoljuk az inverz függvényét és inverz függvényének a deriváltját, a függvény mindenhol konvex, vagy mindenhol konkáv, akkor az alábbi sorozat határértéke tart a függvényünk értékéhez az x0 helyen:
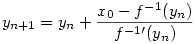
Ebből ki is jön n. gyökre a babilóniai módszer.
|
| Előzmény: [411] Sirpi, 2008-04-04 14:19:18 |
|
|
| [423] epsilon | 2008-04-07 19:41:32 |
 Helló! Megint van egy kedves feladat, látszatra jámbor:
|
 |
|
|
| [421] Sirpi | 2008-04-07 18:38:22 |
 Nem megy máshogy. A kettő teljesen ekvivalens: ha mondasz k-t és l-et, én megmondom x-et és y-t, és fordítva.
Ha nagy számokat akarsz felbontani, akkor amire rákereshetsz, mert sokkal jobban működnek, minthogy  -ig megnézünk minden prímet, hogy osztja-e n-t: -ig megnézünk minden prímet, hogy osztja-e n-t:
Pollard  -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk. -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.
|
| Előzmény: [418] csewe, 2008-04-07 14:59:55 |
|
|
| [418] csewe | 2008-04-07 14:59:55 |
 tulajdonképpen amint látom nekem n - et fel kel lbontanom "fejben/papiron" két szám szorzatára.
akkor viszont nem igen jutottam elöbre , mert ez nagyob számoknál már gondot okozhat. nincs más megoldás?
mert n felbontása csak találgatással megy.
|
| Előzmény: [420] Sirpi, 2008-04-07 13:42:32 |
|
| [420] Sirpi | 2008-04-07 13:42:32 |
 Oké, hogy csak páratlanra kell, de pl. a 10-et vagy a 42-t írd fel ilyen szorzat alakban, nem fog menni. Ahogy írtam, a 4-gyel oszthatók mennek, a csak 2-vel, de 4-gyel nem oszthatóak pedig nem.
Páratlanra meg úgy megy, ahogy írtam: n-et felbontod k.l-re, és innen 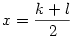 , ,  . .
Példa: n=91=7.13, ekkor 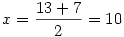 , , 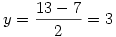 , és tényleg: 91=(10+3).(10-3) , és tényleg: 91=(10+3).(10-3)
|
| Előzmény: [417] csewe, 2008-04-07 12:50:16 |
|






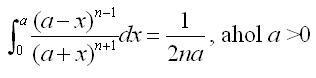






 -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.
-módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.