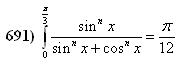| [527] Csimby | 2008-05-20 15:58:38 |
 Én úgy emlékszem általános iskolában nem volt se páros, se páratlan. Egyetmen páros. Gimiben is páros. De hogy a 0 természetes szám-e, az előadónként változik :-)
|
|
| [526] rizsesz | 2008-05-20 15:53:28 |
 A -400 pedig nem egy racionális szám négyzete... Szerintem a matematika egy abszolút logikus dolog, ahogyan az már korábban kiderült, pl. a 11-szög szerkesztéses témában. Szerintem nincsen értelme arról beszélni, hogy a 0 páros-e, mert abszolúte nyilvánvalóan az, akármelyik szabály szerint is vizsgáljuk. Hasonló ez ahhoz a kérdéshez, hogy 0 természetes szám-e (itt már csak a kicsit szofisztikált "ha nem lenne az, akkor a pozitív egész szám elnevezésnek nem lenne értelme" indoklás győtött meg engem a megállapodásokon túl :))
|
| Előzmény: [525] BohnerGéza, 2008-05-20 15:23:16 |
|
|
|
|
| [522] Sirpi | 2008-05-20 08:08:14 |
 Gondolom a plusz jelek helyett is csillagokat kell érteni.
Teljes indukcióval könnyen igazolható az állítás, nevezetesen:
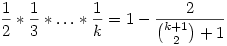
Ha k=2, akkor 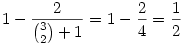 , tehát az állítás igaz. , tehát az állítás igaz.
Most bizonyítsuk k-1-ről k-ra:
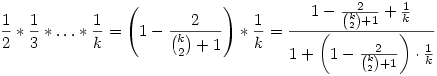
Bővítsünk a két nevező szorzatával:
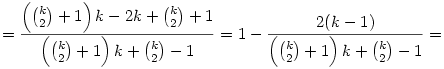
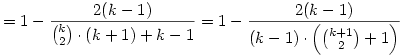
Itt (k-1)-gyel lehet egyszerűsíteni, és be is bizonyítottuk az állítást.
|
| Előzmény: [519] epsilon, 2008-05-19 20:24:41 |
|
|
| [520] dadika | 2008-05-19 22:07:26 |
 Köszönöm a választ.
Igen, minden oldalról közelítve párosnak tűnik. Nekem viszont egyszer egy tanár azt mondta, hogy se nem páros, se nem páratlan(lehet, hogy rosszul emlékszek) A matek szóbeli tételnél jött elő, nem a rulettre gondoltam.
|
| Előzmény: [513] SmallPotato, 2008-05-19 13:58:23 |
|
| [519] epsilon | 2008-05-19 20:24:41 |
 Helló! Még van egy szaporátlan feladat, jó lenne valami szabály ennek az elvégzésére! Előre is kösz, üdv: epsilon
|
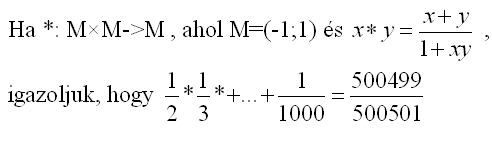 |
|
|
| [517] epsilon | 2008-05-19 18:23:43 |
 Helló! Köszi Káli gúla! Valóban, így még ha "határérték szagja" is van, de meg lehet "lobbyzni"! ;-) Üdv: epsilon
|
|
|
| [515] epsilon | 2008-05-19 15:57:41 |
 Pontosabban az a gondom vele, hogyaz a=b egyenlőséget limesszel tudtam bizonyítani. Vázolom: legyen x=1-1/n és y=-1+1/n. Ezeket beírva a * műveletve, a határárték [-1;1] közöt kellene legyen, ellenben a tört nevezője a 0-hoz tart, a számláló pedig (a-b)-hez, így véges határérték csak a 0/0 határozatlan esetből adódhat. Tehát szükséges, hogy a=b legyen. Tényleg nem jönne össze analízis nélkül? Üdv: epsilon
|
|
| [514] epsilon | 2008-05-19 15:49:58 |
 Helló! Megint akadt egy látszatra könnyű feladat,bármilyen ötletet szívesen várok! Előre is kösz, epsilon
|
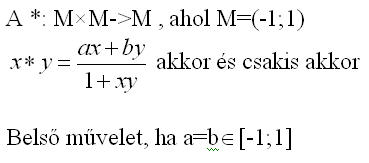 |
|
| [513] SmallPotato | 2008-05-19 13:58:23 |
 Engem (is?) érdekelne, hogy milyen apropóból merült fel ez a kérdés.
Végülis ha "definíció" szerint nézzük, akkor is páros (azaz 2-vel osztva 0 maradékot ad), ha "emberi" módon nézzük (kettesével lépkedve egy nem-0 páros számtól indulva), akkor is páros ...
A rulett kétségkívül más - a kártyához hasonlóan, ahol az alsó és a felső társai nem az elülső, hátulsó és az oldalsó, hanem a király és az ász. :-)))
|
| Előzmény: [511] dadika, 2008-05-19 12:01:27 |
|
|
| [511] dadika | 2008-05-19 12:01:27 |
 Sziasztok!
Egy nagyon egyszerű kérdésre szeretnék választ kapni, a 0 az páros szám, vagy se nem páros se nem páratlan.
|
|
| [510] Káli gúla | 2008-05-18 19:33:14 |
 Az egyenletet felírhatod abból kiindulva is, hogy a belső szögfelező egyenesének normálvektora a külső szögfelező iránya, ez pedig az oldalirányú egységvektorok különbsége: ÿ 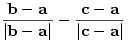 (|v| a vektor hosszát jelenti). Tehát a keresett egyenlet: (|v| a vektor hosszát jelenti). Tehát a keresett egyenlet:
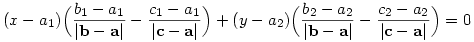
|
| Előzmény: [507] komalboy, 2008-05-18 11:45:52 |
|
|
|
| [507] komalboy | 2008-05-18 11:45:52 |
 Sziasztok!
Valaki leírná általánosan a háromszög egyik belső szögének szögfelező egyenesének egyenletét??? előre is köszönöm
|
|
| [506] epsilon | 2008-05-02 20:12:36 |
 Helló Róbert Gida! A 659)-es feladatra ennél szebb, egyszerűbb megoldást elképzelni sem lehet, gatulálok, köszi! a 691)-es feladat esetén valóban úgy tűzték ki, hogy a limeszét kérték, de Én blöffnek láttam, minekutána az [503]-nál vázoltam a gondolatmenetet, hát azt nagyon át kell néznem, hogy miért hibás az, hogy egyenként kijön az a 6 integrálnak a közös pi/12 érték, de lehet, hogy nem hibás, hanem a limesszel már másként alakul. Szóval jó sejtésed volt, hogy a limeszt odatetted. Szóval most azt a megoldást is alaposa átmazyolázom, haddlám mit tévesztettem szem elől, a társintegráljaim esetén. Mindenképpen, ez a megoldásod lényegesen rövidebb mint amibe Én belekezdtem. Gratulálok, és kösz, üdv: epsilon
|
|
|
| [504] Róbert Gida | 2008-05-02 16:50:47 |
 De persze csak n tart végtelen esetén lesz annyi az integrál, adott n-re nem annyi. Számlálóval beosztva szebb az integrál:
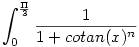
Ami így írva már kellemes, hiszen 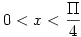 esetén 1<cotan(x), míg esetén 1<cotan(x), míg 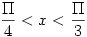 esetén 0<cotan(x)<1. Rögzített esetén 0<cotan(x)<1. Rögzített  >0-ra, amit integrálni kell az tart 1-hez a >0-ra, amit integrálni kell az tart 1-hez a ![[\frac {\Pi}{4}+\epsilon,\frac {\Pi}{3}]](keplet.cgi?k=D593301CFAF47485) intervallumon, így az integrál intervallumon, így az integrál 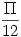 -höz tart. Míg -höz tart. Míg ![[\epsilon,\frac {\Pi}{4}-\epsilon]](keplet.cgi?k=4F33B6E6E51CB10C) intervallumon 0-hoz tart, így az integrál is. A kimaradó két intervallum hossza 0-hoz tart, de rajta korlátos függvényt integrálunk, így az integrál is 0-hoz tart, ha intervallumon 0-hoz tart, így az integrál is. A kimaradó két intervallum hossza 0-hoz tart, de rajta korlátos függvényt integrálunk, így az integrál is 0-hoz tart, ha  tart 0-hoz. Így az integrál tart 0-hoz. Így az integrál 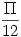 . .
|
| Előzmény: [503] epsilon, 2008-05-02 15:29:53 |
|
| [503] epsilon | 2008-05-02 15:29:53 |
 Helló! A feltételezhetően utolsó (?) integrál az alábbi: ezzel az a gond, hogy nagyon hosszas, és az eredmény duplája az-az pi/6 jött ki a pi/12 helyett. A megoldásvázlat: Legyen I ugyanaz az integrál mint a képen, de 0 és pi/2 között. Ezt felbontottam I=I1+I2+I3 integrálokra, pi/6 és pi/3 osztópontoknál. Hozzárendeltem a J=J1+J2+J3 társintegrálokat, amik ugyanolyanok mint az előzőek, de a számlálókban sin helyett cos van. Nem nehéz igazolni, hogy I=J=pi/4. Ezután változócseréket végeztem és I1=J3, és ilyesmik adódtak. Az lett a vége, hogy mind a 6 számozott integrál egyenlő, és közös értékük pi/12. De ezzel, a kitűzött feladat integrálja I1+I2=pi/6 és nem pi/12 :-( A megoldásom hibás, vagy a kitűzött feladatban a felső korlát pi/6 kellene legyen a pi/3 helyett? Vagy ??? Ez a feladat, kösz, üdv: epsilon.
|
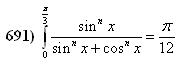 |
|







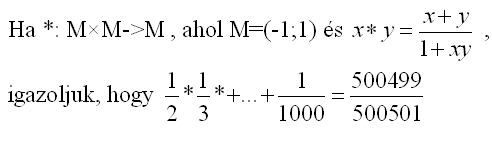

 (0,1), akkor a=b. Szorozd meg (1-x2)-tel: |a-b|x<1-x2. Ez csak úgy lehet, ha |a-b|=0. Persze el lehet mondani határértékkel is, de egyszerűbb lerajzolni.
(0,1), akkor a=b. Szorozd meg (1-x2)-tel: |a-b|x<1-x2. Ez csak úgy lehet, ha |a-b|=0. Persze el lehet mondani határértékkel is, de egyszerűbb lerajzolni. 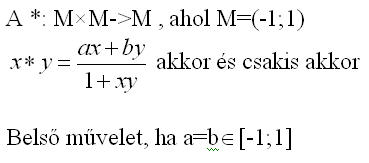



 ),b*sin(
),b*sin( >0-ra, amit integrálni kell az tart 1-hez a
>0-ra, amit integrálni kell az tart 1-hez a