| [590] jonas | 2008-09-16 15:55:46 |
 Azt hiszem, erről valaki olyan algebristát kell megkérdezni, aki emlékszik valamire a csoportelméletből, vagy a szimmetrikus struktúrák vagy blokkrendszerek vagy hasonló nevű tárgyakból. Én szimmetrikus struktúrákat nem hallgattam, csoportelméletről pedig csak papírom van, de nem értek hozzá, ezért nem hiszem, hogy tudnék válaszolni. Lehet, hogy más valaki a fórumon tud segíteni; ha nem, akkor gondolom keresned kell valakit a fórumon kívül, aki ért ilyesmikhez.
|
| Előzmény: [585] jenei.attila, 2008-09-15 11:31:41 |
|
| [589] jenei.attila | 2008-09-16 14:29:33 |
 Ez így van. Nekem viszont m=6 bármely ponton át kéne lehetőleg egy egyens, amely legfeljebb k=12 pontot tartalmaz. Ez már nem affin sík lesz (mivel 6 ponton át általában nem húzható egyenes), de nem is annyira elméletileg, mint gyakorlatilag érdekelne a feladat. Legalább 8815 12-es beosztás kell, de egyáltalán nem biztos, hogy ennyiből megoldható. Ha ennek kb. kétszeresével megoldható, még az is jó.
|
| Előzmény: [588] Fálesz Mihály, 2008-09-16 14:19:44 |
|
|
|
|
| [585] jenei.attila | 2008-09-15 11:31:41 |
 Az Új matematikai mozaik c. könyvben Montágh Balázs írt egy fejezetet Salakmotor-versenyek és véges síkok címmel.Itt azt vizsgálja, hogy n versenyzőt hogy lehet k versenyzőből álló futamokba beosztani úgy, hogy bármely két versenyző egy futamban összemérje magát. Engem egy kicsit általánosabban érdekelne a probléma, vagyis bármely m versenyző (m<=k)legalább egy futamban együtt induljon. Nem kell feltétlenül csak egy futamban elindulni adott m versenyzőnek, de persze ez lenne a legjobb. A futamok sem kell, hogy pontosan k versenyzőből álljanak, lehet kevesebb is (de legalább m). A cél, hogy a lehető legkevesebb futam legyen, és bármely m versenyző legalább egy futamon együtt induljon el. Ha ez elméletileg nehéz lenne, akkor egy közel optimális megoldás is megfelel, illetve egy algoritmus is, amely egy megfelelő beosztást generál.
|
|
| [584] nadorp | 2008-09-10 09:11:03 |
 Van egy olyan érzésem, hogy az eredeti feladatban a bal oldalon -x2+4x-3 volt. Erre utal az is, hogy a "Versenyvizsga portálon" is fenn van példa szerintem szintén rosszul ( 1994 II kat. első forduló 3. feladat), úgy ahogy Te írtad, de az ott közölt megoldásban a fenti másodfokú polinomra hivatkoznak.
|
| Előzmény: [582] S.Ákos, 2008-09-09 20:43:10 |
|
|
| [582] S.Ákos | 2008-09-09 20:43:10 |
 Sziasztok! Régi oktv-feladat a következő egyenlet:
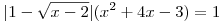
(x valós) Valaki tudna segíteni, mert kb. semmit nem tudtam vele kezdeni?
|
|
| [581] enyac | 2008-09-06 07:36:18 |
 Köszönöm szépen, a kapott ab-ab=0 kifejezés már sokkal szimpatikusabb volt... :-) Elég régen nem tanultam már matekot, de szép lassan azért eszembe jutnak a dolgok... ;-)
|
| Előzmény: [580] BohnerGéza, 2008-09-05 20:16:09 |
|
|
| [579] enyac | 2008-09-05 18:15:12 |
 Tiszteletem!
Egy feladat megoldásában szeretnék sürgős segítséget kérni...
Nekem úgy tűnt, hogy mivel a-szor a van a nevezőben is, ill. a számlálóban is, így azok kiejtik egymást, marad b-b, ami nullvektor... Mit gondolok rosszul?
Köszönöm szépen a segítséget előre is!
|
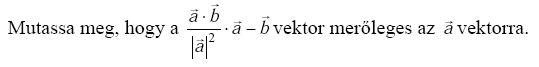 |
|
|
|
|
|
|
| [573] BohnerGéza | 2008-07-16 11:50:27 |
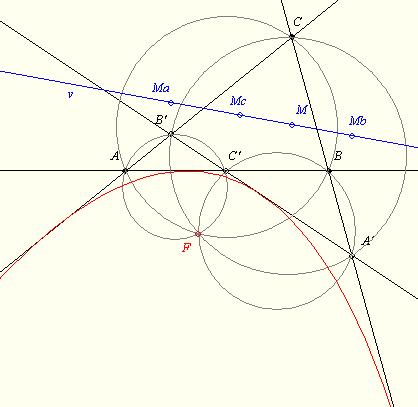
 Az általad megfogalmazott feladat pontosabban talán:
Ha négy egyenes négy háromszöget alkot, akkor ezek magasságpontjai egy egyenesen vannak, körülírt köreik egy ponton mennek át. ( Nem tudtam, de ez speciális esetben a Miquel-pont ) Ez a pont és a magasságpontok egyenese parabolát határoz meg, melynek az eredeti 4 egyenes érintője.
|
 |
| Előzmény: [570] zsolla, 2008-07-16 07:34:57 |
|
|
| [571] sakkmath | 2008-07-16 10:23:15 |
 Szerintem a Miquel-tételkört keresed (q  g). Keresd fel a Geometrikont itt. Klikkelj az M-betűre. A megjelenő, sorszámozott témakörök között a 410. a Miquel-pont, de érdemes megnézni a 407., 411. tételköröket is. g). Keresd fel a Geometrikont itt. Klikkelj az M-betűre. A megjelenő, sorszámozott témakörök között a 410. a Miquel-pont, de érdemes megnézni a 407., 411. tételköröket is.
|
| Előzmény: [570] zsolla, 2008-07-16 07:34:57 |
|
| [570] zsolla | 2008-07-16 07:34:57 |
 Valahogy igy lehetne, de szeretném pontosabban:
Ha a síkon felveszünk 4 egyenest, hogy azok 6 pontban metszék egymást, és 3 háromszöget alkossanak, majd megrajzoljuk a háromszögek köré írható köröket, akkor a körök egy pontban találkoznak, amit Miguel pontnak neveznek.
|
|
|
|
| [567] zsolla | 2008-07-15 20:29:01 |
 Pontosan meg tudná valaki határozni, hogy mit értünk Miguel ponton?
|
|
|









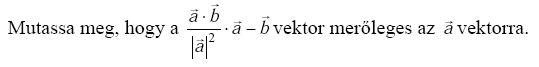




 g). Keresd fel a Geometrikont
g). Keresd fel a Geometrikont