| [724] epsilon | 2008-12-20 11:24:27 |
 Tisztelt Kollégák! A maradékosztályok modulon halmazon értelmezett + és × által képezett (Z(n), +, ×) gyűrűn szeretném tárgyalni az ax+by=c Diofantikus, az elsőfokú 2 ismereltenes 2 egyenletből álló, valamint az elsőfokú 3 ismeretlenes 3 egyenletből álló egyenletrendszerek megoldhatóságát. Tudna-e Valaki valamilyen netes információt adni, vagyis linket adni, ahol ezekről olvashatok, magyar, francia vagy angol nyelven. Előre is köszönöm, üdv: epsilon
|
|
|
|
| [721] Ágoston | 2008-12-08 17:56:55 |
 A mostani kömal B. 4122.ben "A piros mezők közül kettő a tábla szélén van". Ez azt jelenti, hogy legalább kettő, vagy azt, hogy pontosan kettő?
|
|
| [720] HAnonymus | 2008-12-07 20:29:07 |
 Köszi a segítséget, megnyugodtam. :)
|
|
| [719] leni536 | 2008-12-07 16:07:05 |
 A differenciálegyenletet jól írtad fel, a megoldásodat visszaírva kielégíti a differenciálegyenletet és a kezdeti feltételeket is, megvan a két szabadsági fok is, úgyhogy jó valószinűleg. Erre a típusú diffegyenletre mi v(x)-et kerestük és vezettük vissza vele elsőfokúakra, azzal is ez jön ki.
|
| Előzmény: [718] HAnonymus, 2008-12-04 13:39:06 |
|
| [718] HAnonymus | 2008-12-04 13:39:06 |
 Sziasztok!
Egy differenciálegyenletes feladatban szeretnék segítséget kérni.
A következő lenne: Egy 6 m hosszú lánc súrlódás nélkül csúszik az asztalon. Ha a csúszás akkor kezdődik, amikor már 1m-nyi lánc lóg lefelé, akkor mennyi idő múlva esik le a lánc? (Feltesszük, hogy az asztal legalább 6 m magas lábakon áll.)
Ötletem az van rá, csak szerintem hibás a gondolatmenetem, szívesen venném ha valaki véleményezné.
Abból indulok ki hogy leesésnek az számít amikor az utolsó láncszem is lefut az asztalról.
Sajnos TeX-használatban nem állok sehogy, úgy találtam egyszerűnek a dokumentálását ha képként elmentem azt ahogy megoldottam, és felteszem egy tárhelyre: ide
Örülnék ha valaki véleményezné, vagy akár teljesen máshogy megoldaná. Köszönöm előre is a segítséget.
Üdv: egy ZH-ra készülő amatőr. :)
|
|
|
|
| [715] leni536 | 2008-12-02 21:07:02 |
 "Érezhető", hogy ha egy konvex síkidom magába foglal egy nála kisebb konvex síkidomot, akkor a külső síkidom kerülete nagyobb, mint a másik síkidom kerülete. Létezik erre tétel? Van erre közismert bizonyítás?
|
|
| [714] Euler | 2008-11-30 19:53:29 |
 Az eredményt konkrétan nem mondom meg, mert nem számoltam végig, de az eljárás a következő:a nevezőben ird fel a nevezetes szorzatot, majd bonts parciális törtekre, ennek módszere több helyen is megtalálható, pl. Bárczy Barnabás: Integrálszámitás c. könyvében is. Innen már "könnyű" a feladat, remélem elég segitséget adtam a feladat megoldásához.
|
| Előzmény: [711] sandor720, 2008-11-29 17:28:56 |
|
| [713] sandor720 | 2008-11-30 12:40:14 |
 Szia!
A mapel-re gondoltál Robert Gida? Az ha jóltudom nem vezeti le csak a megoldást mutatja meg!
|
|
|
| [711] sandor720 | 2008-11-29 17:28:56 |
 Köszönöm a segitséget! Vola itt még egy feladat
|
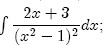 |
|
|
|
| [708] sandor720 | 2008-11-29 13:36:32 |
 sziasztok!
Köszönöm a segitségeteket integráláshoz nem tudom levezetni melyik szabály alkalmazható a:
|
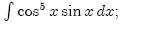 |
|
| [707] Gyöngyő | 2008-11-26 21:21:24 |
 Szia!
Amit csináltam megoldást az pontosan az amit most leirtál. Azt mondta rá a tanárom,hogy szerinte sincs egyszerűbb megoldás.Majd megprobálom feltölteni a megoldásomat,ha sikerül,csak most ezzel a konvex geometriai feladattal szenvedek.
Üdv.: Gyöngyő
|
| Előzmény: [706] sakkmath, 2008-11-26 18:54:21 |
|
| [706] sakkmath | 2008-11-26 18:54:21 |
 Kiegészítés: A (2) egyenlőtlenség bal oldalán álló kifejezés t-nek páros függvénye, ezért elég az egyenlőtlenséget t 0-ra bebizonyítani. Ekkor az alkalmazott 0-ra bebizonyítani. Ekkor az alkalmazott 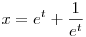 helyettesítés már egy-egy értelmű megfeleltetést létesít az x-ek t-k halmaza között, hiszen az x(t)=2cht függvénynek csak az első síknegyedbe eső, szigorúan monoton növekedő részével van dolgunk. helyettesítés már egy-egy értelmű megfeleltetést létesít az x-ek t-k halmaza között, hiszen az x(t)=2cht függvénynek csak az első síknegyedbe eső, szigorúan monoton növekedő részével van dolgunk.
Egy kérdés Gyöngyőhöz: Születtek-e a feladatra más, egyszerűbb megoldások?
|
| Előzmény: [654] sakkmath, 2008-10-31 17:17:06 |
|
| [705] Gyöngyő | 2008-11-26 16:27:58 |
 Sziasztok! Az alábbi két feladathoz szeretnék segítséget kérni:
1.:Vesszük az összes konvex centrálszimmetrikus sokszöget.Az a kérdés hogy milyen határok között változik a kerülete,ha a saját normájában nézzük.Pl. ha a négyszöget nézzük akkor a négyszög normában mekkora a kerülete.
2.:Mekkora az azonos centrumú szabályos n-szög és kör Hausdorf távolsága?
Köszi elöre is. Gyöngyő
|
|
|
| [703] j.milan | 2008-11-23 22:42:50 |
 Ez szerintem nem működik, csak bejelentkezett felhasználók esetén. De nekem ez a problémám, hogy nem tudok belépni. Ezt a regisztrációt azért hoztam létre, hogy a fórumon tudjak segítségt kérni az eredeti accom elfelejtett jelszava miatt.
|
| Előzmény: [700] nadorp, 2008-11-23 21:25:17 |
|
|
|
|







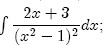


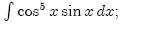

 0-ra bebizonyítani. Ekkor az alkalmazott
0-ra bebizonyítani. Ekkor az alkalmazott  =1 jó. Általában sok megoldás létezik. Adott v-hez és
=1 jó. Általában sok megoldás létezik. Adott v-hez és