| [820] Lóczi Lajos | 2009-02-22 17:23:04 |
 Viszont igazzá válik az állítás, ha megköveteljük, hogy a két végpontban ugyanazok legyenek a függvényértékek, vagyis f(a)=g(a) és f(b)=g(b) legyen.
Ekkor ugyanis a két konvex alakzat tartalmazni fogja egymást (az egyik alakzat a két végpont, az őket összekötő szakasz és f "lelógó" grafikonja által határolt síkidom; a másik ugyanígy, csak g-vel), és ismert (itt a Fórumon már kétszer is előkerült a bizonyítása, csak meg kell keresd :), hogy ha egy konvex alakzat tartalmaz egy másikat, akkor a külső alakzat kerülete nem lehet kisebb.
|
| Előzmény: [818] M. Feri, 2009-02-22 13:45:13 |
|
| [819] plac | 2009-02-22 14:22:15 |
 Hello! A kérdésem a következő lenne. Valaki megtudja nekem mondani, hogy fn(x)=x.arctan(nx), H=(0, ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni. ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni.
|
|
|
|
| [816] M. Feri | 2009-02-22 12:54:29 |
 Sziasztok! A következő feladatban valami hiba van, vagy én vagyok figyelmetlen? (Szerintem hiányzik még egy feltétel): Ha f és g [a,b] intervallumot leképezi a valós számok halmazára, mindkét függvény konvex, deriválható és deriváltjai folytonosak, emellett még f(x) g(x) akkor g(x) akkor 
Megoldható így, ebben az alakban? Ha igen, hogy? Előre is köszönöm!!
|
|
| [815] laci777 | 2009-02-22 00:21:36 |
 Ha nem baj, megint egy példával jönnék, kifogni látszik rajtam. Egy egyenletes v1 sebességgel haladó, 1 km hosszú menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott 15 mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont 1 km-t tesz meg. A kérdés, mekkora utat tett meg a futár összesen?
Azt látom, hogy a 15 mp-ben megtett, 0<s<1 km út függvényében egyre nagyobb a szükséges v2-v1 sebességkülönbség, ill. hogy a futár összteljesítménye 2 és 3 km (pontosabban 1+gyökkető és 3) km között kell legyen, de a megoldáshoz vezető másodfokú egyenlet (legalábbis nagyon remélem, hogy az) túl kemény dió:(
Még az itt felvetett többi probléma nehézségét látva is remélem, most is lesz, aki segít a megoldásban:)
Előre is köszönöm.
|
|
| [814] HoA | 2009-02-20 10:29:29 |
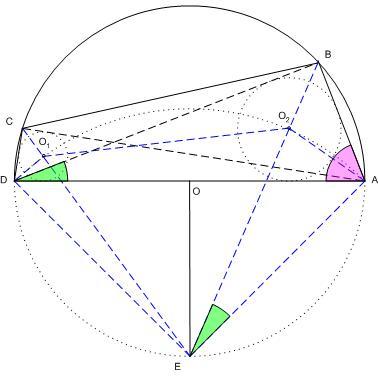
 Ha az a bizonyos Thálesz-kör egységsugarú és a "Thales körbe írható derékszögű háromszögek beírt körök középpontjai köre" [803] ábrájának AO2O1D körívét jelenti, O1ésO2 pedig az ACD ill. ABD háromszögek beírt köreinek középpontját, akkor az első válasz igen, BC mindig gyök 3. Ugyanis a körív sugara 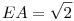 , ezért ebben az esetben EO1O2 háromszög szabályos, E-nél lévő szöge 60o. Mivel az EO1ésEO2 egyensek egyúttal a C-nél ill. B-nél lévő derékszögek felezői, így az általuk bezárt szög 60o, tehát BC az egységsugarú körnek 60o-os kerületi szöghöz tartozó húrja, ez pedig , ezért ebben az esetben EO1O2 háromszög szabályos, E-nél lévő szöge 60o. Mivel az EO1ésEO2 egyensek egyúttal a C-nél ill. B-nél lévő derékszögek felezői, így az általuk bezárt szög 60o, tehát BC az egységsugarú körnek 60o-os kerületi szöghöz tartozó húrja, ez pedig  hosszú. hosszú.
Ha O1O2 forog, BC is mozog, de nem együtt, "merev test szerűen" forognak. [755] és [803] ábrájának összehasonlításából látható, hogy szimmetrikus esetben O1O2 és BC párhuzamosak, egyébként nem. Szemléletesen úgy képzelhető, hogy a rögzítetten 60o-os O2EO1 szög két szára forog legyezőszerűen, és bármely helyzetében a 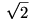 sugarú AO2O1D körívből 60o-os középponti szöghöz tartózó sugarú AO2O1D körívből 60o-os középponti szöghöz tartózó 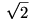 hosszúságú O1O2 húrt, az egységsugarú Thálesz-körből pedig 60o-os kerületi szöghöz tartózó hosszúságú O1O2 húrt, az egységsugarú Thálesz-körből pedig 60o-os kerületi szöghöz tartózó  hosszúságú BC húrt metsz ki. hosszúságú BC húrt metsz ki.
|
| Előzmény: [810] kiskiváncsi, 2009-02-19 20:24:56 |
|
|
| [812] jenei.attila | 2009-02-19 23:22:26 |
 Van-e a valós számok additív csoportjának nem triviális automorfizmusa?
Van-e a valós számok testének véges, vagy megszámlálható indexű részteste? Egyáltalán continuum számosságú valódi részteste? Mi a "legbővebb" valódi résztest?
Nem tudom a válaszokat, valaki segíthetne.
|
|
| [811] nadorp | 2009-02-19 23:10:40 |
 Én a bizonyításod megfogalmazására gondoltam.
Ha azt mondod:
"Tekintsünk egy a,b,c oldalú háromszöget, melyre fennáll az egyenlőség. Ekkor a cosinus tétel szerint ebben a háromszögben a c-vel szemben 60o van, tehát c a "középső" hosszúságú oldal."
akkor a fenti bizonyítás hiányos, mert nem tudjuk, hogy létezik-e az a,b,c oldalú háromszög.
Ha viszont azt mondod:
"Tekinsünk két pozitív a b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet." b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet."
akkor jó a megoldásod.
|
| Előzmény: [807] laci777, 2009-02-19 19:30:30 |
|
| [810] kiskiváncsi | 2009-02-19 20:24:56 |
 Kedves HOA! Ez a feladat az egyik fórumon így jelent meg: O1O2 gyök2 hosszú szakasz a Thales körbe írható derékszögű háromszögek beírt körök középpontjai körén foroghat. Mekkora a BC szakasz? Azaz ez a megadott és csak ez létezik, vagy kinetogeometriailag ki lehet szerkeszteni, BC valóban mindig gyök 3 vagy nem? Azaz ha O1,O2 szakasz forog, akkor BC állandó és egyenlő gyök3? Vagy csak ez a 6o fokhoz tartozó két szakasz együtt foroghat (merev test szerűen)?
|
|
| [807] laci777 | 2009-02-19 19:30:30 |
 Nem tudom, jól értettem-e, amit írtál, kedves Nadorp, de pl. az (1;2;gyökhárom) számhármas esetén létezik a háromszög (bármely két oldal nagyobb a 3.-nál), és az egyenletet is kielégíti.
Vagy inkább arra utaltál, hogy a jelzett végtelen sok megoldás is csak részmegoldás, azaz létezhet olyan számhármas is, amivel az egyenlőség ugyan igaz, de háromszöget nem lehet ezekből kialakítani? Mindenesetre megpróbálok ezen is gondolkodni, mert volt kis hiányérzetem e tekintetben - de mivel a feladat azt kérte, hogy "írjuk fel növekvő sorrendben a számokat", úgy gondoltam, hogy már létező háromszögek esetén is végtelen sok megoldás adható. Ha viszont az "a", a "b" és a "c" egymáshoz képesti sorrendjét kérdezi, akkor csak a "c" köztes helyzete állapítható meg.
Vagy végképp tévúton járok?
|
| Előzmény: [806] nadorp, 2009-02-19 17:06:38 |
|
|
| [805] laci777 | 2009-02-19 16:29:02 |
 Sziasztok! Most egy már megoldott(?) versenypéldával kapcsolatban kérném szépen véleményeteket.
Vegyük a köv. egyenletet: a2+b2-ab=c2 (ahol a,b,c páronként különböző pozitív valósak). A feladat: fel kell írni növekvő sorrendben a számokat. Arra jutottam, hogy egy olyan háromszög oldalairól van szó, ahol - a koszinusztétel miatt - a c oldallal szembeni szög 60 fok, és a<c<b vagy b<c<a. Ugyanakkor végtelen sok számhármas kielégíti a feltételeket (pl. 1, 2, gyökhárom ill. ezek tetszőleges k-szorosa hasonló derékszögű háromszögek esetén, és akkor még ott van végtelen sok egyéb lehetőség, ahol alfa és béta együtt 120 fok). De - ha minden igaz - ez nem jó (nem teljes?) megoldás. De miért? Tényleg szeretném tudni.
|
|
| [804] sakkmath | 2009-02-17 13:20:30 |
 Örülök, hogy a rajzoddal talpra állítottál, az újbóli fejreállást egy tengelyes tükrözéssel megoldom :))
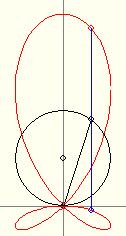
Az adott tulajdonságú pontok halmaza egy negyedrendrendű algebrai görbe (a rajzodon még két további metszéspont is bejelölhető...), melynek egyenlete - Descartes-koordinátarendszerben - implicit és explicit módon is megadható... (Utóbbi esetben a görbét több, csatlakozó ívre kell bontani.)
Egykor hosszas nyomozást folytattam annak megállapítására, hogy hol, mikor fedezték fel ezt a görbét. Az eredmény: a trifolium (lóhere) nevű görbecsalád egy speciális esetéről van szó (legalábbis ezt írta a Encyclopedia Britannica ). Az általánosabb főgörbé(ke)t egyébként nem az általam talált szerkesztéssel definiálták.
Bebizonyítható, hogy a görbe által határolt terület kétszerese a kiindulási kör területének. Nekem ez "csak" integrálszámítással sikerült. Kérdés: van-e erre egy elegánsabb módszer?
A görbével kapcsolatban több egyéb kérdés is feltehető és megválaszolható. Pl.: súlypontok, megforgatással kapott test térfogata, stb. A K kerület viszont ellenállt, ez szerintem csak közelítő módszerekkel határozható meg. Nálam K/a  14,1666. 14,1666.
|
| Előzmény: [802] BohnerGéza, 2009-02-16 19:48:30 |
|
| [803] HoA | 2009-02-17 12:53:30 |
 [757] ábrája arra utal, hogy használjuk fel: a háromszög beírt körének középpontja rajta van például a b oldal  /2+ /2+ /2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol /2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol  szögfelezője is metszi a körülírt kört. Az itt mellékelt ábra jelöléseivel EA=EO2 egyenlőséget közvetlenül is beláthatjuk. Legyenek az ABD háromszög szögei szögfelezője is metszi a körülírt kört. Az itt mellékelt ábra jelöléseivel EA=EO2 egyenlőséget közvetlenül is beláthatjuk. Legyenek az ABD háromszög szögei  , , , , . Ekkor AEB . Ekkor AEB  = = ( BA húrhoz tartozó kerületi szög ), DAE ( BA húrhoz tartozó kerületi szög ), DAE  = DBE = DBE  = =  /2,O2 AD /2,O2 AD  = =  /2,O2 AE /2,O2 AE  = = /2+ /2+ /2 és így EAO2 háromszög O2 -nél lévő EO2A szöge is /2 és így EAO2 háromszög O2 -nél lévő EO2A szöge is  /2+ /2+ /2 , EAO2 egyenlőszárú, EA=EO2 . Ugyanez igaz EO1-re is, így O1EO2 egyenlőszárú. /2 , EAO2 egyenlőszárú, EA=EO2 . Ugyanez igaz EO1-re is, így O1EO2 egyenlőszárú.
Csak most használjuk fel, hogy egységsugarú körülírt körről és derékszögű ABD háromszögről van szó:  Az Az 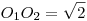 feltétel tehát azt jelenti, hogy O1EO2 feltétel tehát azt jelenti, hogy O1EO2 szabályos, O2EO1 szabályos, O2EO1 =60o , BC az egységsugarú körben 60o-os kerületi szöghöz tartozó húr, hossza így =60o , BC az egységsugarú körben 60o-os kerületi szöghöz tartozó húr, hossza így 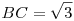
A gondolatmenet megfordítható, ha 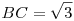 , akkor BEC , akkor BEC =O2EO1 =O2EO1 =60o , O1EO2 egyenlőszárú =60o , O1EO2 egyenlőszárú  szabályos, szabályos, 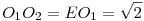
|
 |
| Előzmény: [757] BohnerGéza, 2009-01-24 16:31:35 |
|
|
| [801] sakkmath | 2009-02-16 10:19:18 |
 Ugyanez a kiinduló kör szerepel a következő feladatban is:
Adott az A(0; a) középpontú, a sugarú kör. A kör valamely - az origótól különböző - pontja legyen C. Tekintsük azokat a C-felezéspontú, OA-val párhuzamos szakaszokat, melyek hossza 2OC. Kérdések:
1. Mi a szakaszvégpontok mértani helye, ha C befutja a kört? 2. Mekkora területet zár be a mértani helyet leíró függvény görbéje? 3. Honnan lehet ismerős a kapott görbe? :)
|
| Előzmény: [795] HoA, 2009-02-15 07:45:55 |
|
|
| [799] nadorp | 2009-02-15 14:17:47 |
 2. megoldás
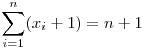 miatt a számtani és harmonikus közép közti egyenlőtlenségből miatt a számtani és harmonikus közép közti egyenlőtlenségből
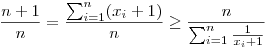 , tehát , tehát

Most felhasználva a mértani és harmonikus közép közti egyenlőtlenséget
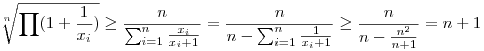
|
| Előzmény: [798] S.Ákos, 2009-02-15 13:56:02 |
|
| [798] S.Ákos | 2009-02-15 13:56:02 |
 Legyen a+b=2p és a-b=2q, ahol a,b,p,q pozitív valós számok. Vizsgáljuk az  kifejezést. a=p+q és b=p-q. Ezekkel a helyettesítésekkel: kifejezést. a=p+q és b=p-q. Ezekkel a helyettesítésekkel:
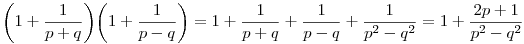
Ha 2p állandó, akkor ez a kifejezés szigorúan monoton nő a [0;p] intervallumon, ha tehát q csökken, akkor a kifejezés értéke is csökken. Ha a számok mind egyenlők, akkor 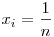 . Ha nem mind egyenlők, akkor van i,j úgy, hogy . Ha nem mind egyenlők, akkor van i,j úgy, hogy 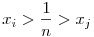 Legyen Legyen 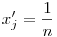 és és 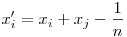 , és a többi xk-t hagyjuk változatlanul. Mivel xi+xj=xi'+xj' és xi>xj'>xj, ezért xi>xi'>xj, így xi-xj>|xj'-xi'|, így a kifejezés értéke csökkent, így a minimum csak x1=x2=...=xn esetén állhat, ami épp a jobb oldal. , és a többi xk-t hagyjuk változatlanul. Mivel xi+xj=xi'+xj' és xi>xj'>xj, ezért xi>xi'>xj, így xi-xj>|xj'-xi'|, így a kifejezés értéke csökkent, így a minimum csak x1=x2=...=xn esetén állhat, ami épp a jobb oldal.
Remélem érthető.
|
| Előzmény: [797] Gyöngyő, 2009-02-15 12:21:18 |
|
| [797] Gyöngyő | 2009-02-15 12:21:18 |
 Sziasztok!
Szeretnék segítséget kérni a következő feladathoz:
Legyenek xi>0,i=1,..,n
x1+x2+...+xn=1. Igazoljuk,hogy :
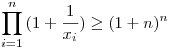
Üdv.: Gyöngyő
|
|
| [796] laci777 | 2009-02-15 11:20:46 |
 Kedves HoA!
Az első megoldásod egyszerű, és így nagyszerű:) A második viszont - a magam szinjéhez képest meg végképp -remekmű. Mindkettőt köszönöm!
|
| Előzmény: [795] HoA, 2009-02-15 07:45:55 |
|
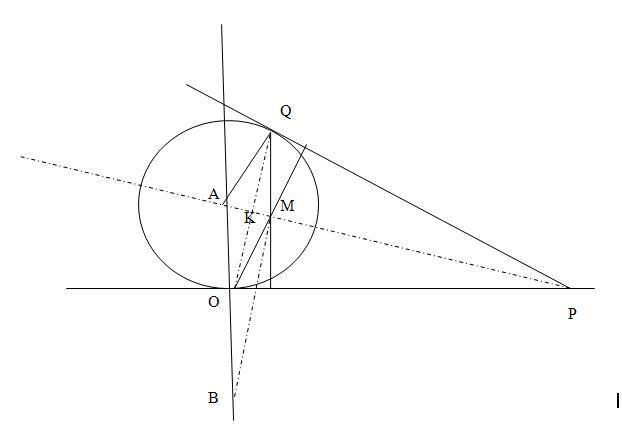
| [795] HoA | 2009-02-15 07:45:55 |
 Legyen a (0;a) pont A, a (0;-a) pont B, a PQO  magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO  derékszögű. Ezt A-ból kétszeresére nagyítva K M-be O pedig B-be kerül. AMB derékszögű. Ezt A-ból kétszeresére nagyítva K M-be O pedig B-be kerül. AMB  derékszögű, tehát M valóban AB Thálesz-körén van. derékszögű, tehát M valóban AB Thálesz-körén van.
Mivel a feladatot koordináta-geometriai megfogalmazásban tűzték ki, oldjuk meg így is. Legyen P (p;0). Q az AP átmérőjű körön van, ennek középpontja (p/2;a/2), sugara 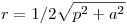 , egyenlete (x-p/2)2+(y-a/2)2=1/4(p2+a2) , (2x-p)2+(2y-a)2=p2+a2 ; 4x2-4xp+p2+4y2-4ya+a2=p2+a2 ; , egyenlete (x-p/2)2+(y-a/2)2=1/4(p2+a2) , (2x-p)2+(2y-a)2=p2+a2 ; 4x2-4xp+p2+4y2-4ya+a2=p2+a2 ;
4x2-4xp+4y2-4ya=0
Q az eredeti körön is rajta van, ennek egyenletét néggyel szorozva 4x2+4(y-a)2=4a2 ; 4x2+4y2-8ay+4a2=4a2 ;
4x2+4y2-8ay=0
A két egyenlet különbségéből a metszéspontokra y/x = p/a ( amit persze az ábráról mint OQ meredekségét könnyen leolvashatunk) , behelyettesítve 4x2+4p2x2/a2-8px=0 Egyik metszéspont az origó, erre nem vagyunk kíváncsiak, x-szel oszthatunk: x(4+4p2/a2)=8p ; x=2p/(1+p2/a2) Ez tehát Q és egyben M abszcisszája (Mx). M ordinátáját (My) abból számíthatjuk, hogy M rajta van az AP egyenesen: x/p+y/a=1 ; y=a-(a/p)x=a-2a/(1+p2/a2)=(a+p2/a-2a)/(1+p2/a2)=(p2/a-a)/(1+p2/a2) . Tekintsük az Mx2+My2 kifejezést:
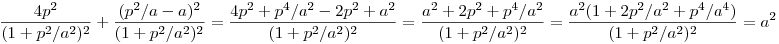 M tehát valóban az origó középpontú a sugarú körön, AB Thálesz körén van. M tehát valóban az origó középpontú a sugarú körön, AB Thálesz körén van.
|
 |
| Előzmény: [794] laci777, 2009-02-14 22:35:15 |
|
| [794] laci777 | 2009-02-14 22:35:15 |
 Megint geometria-példában kérnék szépen segítséget: vegyük az x2+(y-a)2=a2 egyenletű kört (az "a" tetszőleges, de rögzített értékű pozitív valós szám). E körhöz az x tengely egy tetszőleges P pontjából érintőt húzunk (nem az origóba). Ezt az érintési pontot Q-val jelölve,határozzuk meg a PQO(O az origo) háromszög magasságpontját. Ha végighaladunk x tengely valamennyi P pontján, mit adnak ki e háromszögek magasságpontjai? Az látszik, hogy a (0;a) és a (0;-a) pontok által meghatározott szakasz Thalész-köre a megoldás a két előbbi pont nélkül - de bizonyítani már nem tudom. Tudna valaki valamilyen kiinduló pontot, ötletet javasolni? Köszönöm előre is.
|
|




 ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni.
) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni. g(x) akkor
g(x) akkor 
 b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet."
b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet." 
 14,1666.
14,1666. /2+
/2+ /2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol
/2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol  ,
, . Ekkor AEB
. Ekkor AEB  =
= szabályos, O2EO1
szabályos, O2EO1