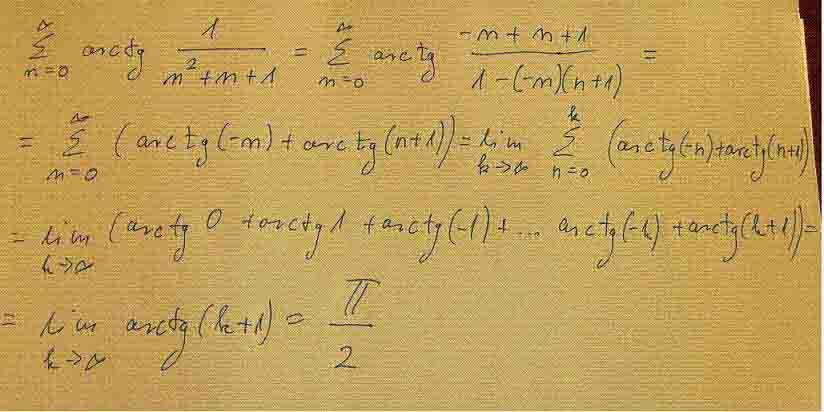|
| [919] Lóczi Lajos | 2009-04-14 19:46:19 |
 De mire kell ez neked? Tegyük fel, itt van előtted egy fájlban a szám. Milyen tulajdonsága érdekel? A számjegyek összege? Hátulról a 26. jegy? Csak azért kérdem, mert lehet, hogy a kívánt információt a teljes alak ismerete nélkül is meg lehet kapni.
|
| Előzmény: [918] Wesselényi-Garay Andor, 2009-04-14 18:59:47 |
|
| [918] Wesselényi-Garay Andor | 2009-04-14 18:59:47 |
 Szia! Köszönöm, szerinted hol érdeklődjem tovább? Kutatóintézetek? Hol van ekkora gép? Az e-mailem: wga418@invitel.hu - esetleg ott is folytathatjuk!
|
|
|
| [916] Wesselényi-Garay Andor | 2009-04-14 15:34:05 |
 Szervusztok!
Lehet, hogy off, de egy - számomra hatalmas - kéréssel/kérdéssel szeretnék hozzátok fordulni. Tudnátok segíteni olyan program, szakértő, stb. megadásában, mely segítségével nagy számokkal lehet dolgozni? Konkrétan egy egyszerű képlet, a 25 a 1312000-en, vagyis "huszonöt az egymillióháromszáztizenkétezrediken" számot szeretném megkapni. Előre is köszönöm, tisztelettel, Wesselényi-Garay Andor
|
|
|
| [914] Cokee | 2009-04-08 20:21:10 |
 Sziasztok!
Milyen n egészre direkt felbonthatatlan Zn?
Üdv.: Cokke
|
|
| [913] zozi | 2009-04-08 14:48:03 |
 közben kiderült ,hogy rosszul adtam meg az értéktatományt így helyes (A + B) < (C / 2)
viszont ezzel az értéktartománnyal nem minden esetben oldható meg az egyenlet kérdésem az lenne , hogy meglehet e tudni hogy mely C értékeknél áll fenn az egyenlősé ,és melyeknél nem
|
| Előzmény: [912] Sirpi, 2009-04-08 12:43:00 |
|
| [912] Sirpi | 2009-04-08 12:43:00 |
 Egy 8-10 jegyű n számnál még simán megy, hogy 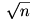 -ig (ami 4-5 jegyű) végignézed az összes számot, hogy osztható-e valamelyikkel. -ig (ami 4-5 jegyű) végignézed az összes számot, hogy osztható-e valamelyikkel.
Egyébként annyi kimaradt az előbb, hogy természetesen a negatív felbontások (pl. (-12).(-1)) is adnak megoldást a feladatra.
|
| Előzmény: [911] zozi, 2009-04-08 10:43:17 |
|
| [911] zozi | 2009-04-08 10:43:17 |
 közben rákérdeztem A is és B is < (C + 1) / 2
a megoldásod egyébként teljesen tuti
de érdekelne , hogy mit lehet tenni 2C felbontása ügyében ha C nagy szám mondjuk 8 10 digites
|
| Előzmény: [910] Sirpi, 2009-04-08 09:19:43 |
|
| [910] Sirpi | 2009-04-08 09:19:43 |
 B.(2A+B+1)=2C
2C-t bontsuk fel egy páros és egy páratlan szám szorzatára (ugyanis B és 2A+B+1 paritása eltérő), az egyik lesz a B, a másik 2A+B+1. így B ismeretében már A is meghatározható.
Példa: C=6
Ekkor 2C-t, vagyis 12-t felbontjuk egy páros és egy páratlan szám szorzatára: 12.1, 4.3, 3.4, 1.12.
Innen B=12,A=-6; B=4,A=-1; B=3,A=0; B=1,A=5
|
| Előzmény: [907] zozi, 2009-04-07 21:00:05 |
|
|
|
| [907] zozi | 2009-04-07 21:00:05 |
 sziasztok
egy ismerősöm megkérdezte , hogy megtudnám e oldani ezt
A*B + B(B + 1) / 2 - c = 0
én azt gondoltam , hogy igen de már három napja ülök rajtra és semmire sem jutottam, bár nem tünik nehéznek, és mostmár nagyon érdekelne , hogy hogyan kell megoldanu.
C -t ismerem A és B -t keresem
|
|
| [906] jonas | 2009-04-06 23:34:15 |
 Én másképpen csinálnám, de az bonyolultabb. Szedjük szét három részre az eseteket a szerint, hogy sorban az utolsó golyó milyen színű: piros, fehér, vagy kék. Jelentse p(x,y,z) a lehetséges gyönygysorok számát, amik x piros, y fehér, és z kék golyóból állnak, és ezek közül az utolsó piros; hasonlóan f(x,y,z) a lehetséges fehérre végződő sorrendek száma, és k(x,y,z) a kékre végződőek száma. Ezekre felírhatóak az alábbi rekurziós összefüggések.
p(x+1,y,z)=p(x,y,z)+k(x,y,z)
f(x,y+1,z)=f(x,y,z)+k(x,y,z)
k(x,y,z+1)=p(x,y,z)+f(x,y,z)+k(x,y,z)
Kivéve hogy a fenti egyenlőtlenségek nem igazak a p(1,0,0)=f(0,1,0)=k(0,0,1)=1 esetekre.
A peremfeltételek a következők.
p(0,y,z)=f(x,0,z)=k(x,y,0)=0
A feladatban a p(2,3,4)+f(2,3,4)+k(2,3,4) érték a kérdés. Ehhez egy táblázatba fell kell írni a p,f,k értékeit minden x,y,z értékhármasra. Ez talán kézzel is kiszámolható, ha nagyon sok türelmed van, de nekem nincs, úgyhogy számítógéppel csinálom. Ez jön ki.

Így aztán az eredmény 60+76+64=200.
Persze számítógéppel egyszerűbb, ha végigpróbálod a 9 golyó mind az 1260 sorrendjét, amiből rögtön látszik, hogy 200 jó.
|
| Előzmény: [902] Sirpi, 2009-04-06 13:17:34 |
|
| [905] Alma | 2009-04-06 23:00:29 |
 Nincs hiba a gondolatmenetedben. A két megoldás ekvivalens, mindkettő helyes elviekben (számítsd ki a hányadosokat, egyezést fogsz kapni, ugyanis a 20! kiesik a két nevezőből)
|
| Előzmény: [904] Valvehead, 2009-04-06 21:04:17 |
|
| [904] Valvehead | 2009-04-06 21:04:17 |
 Egy gép 1400 alkatrészt gyárt egy műszakban, amelyből 50 selejt. Véletlenszerűen kiveszünk egy 20 elemű mintát. Mennyi a valószínűsége, hogy a mintánkban nem lesz egyetlen selejt sem?
A hivatalos megoldás - kedvező eset: 1350.1349.....1331 - összes eset: 1400.1399.....1381
Nem értem, hogy miért veszi figyelembe a sorrendet (ism. nélküli variáció képlete), én azt gondoltam, h. pl. belemarkolok és sorrendtől függetlenül kiveszek egyszerre 20 alkatrészt...
Megoldásom: - kedvező: 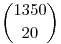 - összes eset: - összes eset: 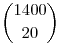
Nagyon hálás lennék, ha vki. elmagyarázná, hogy hol a hiba a gondolatmenetemben.
|
|
|
| [902] Sirpi | 2009-04-06 13:17:34 |
 A két piros helyzete alapján össze lehet számolni az eseteket. Ha a másik két színt nem nézzük, akkor a pirosak 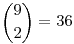 -féleképpen helyezkedhetnek el. Azt kell csak megnézni, hogy az egyes pozíciókban hányféleképpen állhat sorban a többi golyó és ezeket össze kell adni. -féleképpen helyezkedhetnek el. Azt kell csak megnézni, hogy az egyes pozíciókban hányféleképpen állhat sorban a többi golyó és ezeket össze kell adni.
A két golyó szomszédos:
- ha az első két helyen vannak, akkor a 3. kék kell hogy legyen, a maradék hat helyre pedig 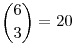 -féleképp kerülhetnek a golyók. -féleképp kerülhetnek a golyók.
- ugyanúgy 20, ha az utolsó két helyen van a két piros golyó (szimmetria miatt).
- ha nem a szélén vannak, ekkor két kék veszi őket körül, és ez a KPPK blokk lehet összesen 6 helyen. Mindegyiknél a maradék 5 golyó  -féleképp helyezkedhet el, ami összesen 60 eset. -féleképp helyezkedhet el, ami összesen 60 eset.
A két golyó másodszomszédos:
- ha az első és a 3. helyen vannak, ekkor PKPK-val kezdődik a sor, ez 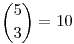 eset. eset.
- ugyanúgy 10, a végén vannak a golyók.
- a közbülső helyeken vannak: ekkor a KPKPK rész lehet 5 helyen, és minden esetben 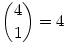 -féleképp helyezkedhet el a többi golyó, ez összesen 20. -féleképp helyezkedhet el a többi golyó, ez összesen 20.
A két piros golyó távolabb helyezkedik el:
- ha a bal oldali piros az első, és a jobb utolsó, akkor PK.....KP alakú a sorrend, 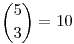 eset. eset.
- ha a bal oldali első, és a jobb nem utolsó (PK..KPK..) a jobb oldali golyó lehet 5 helyen, a maradék helyekre 4-féleképp jöhet a többi golyó, ami 20 lehetőség.
- a jobb oldali az utolsó, a bal nem első: szintén 20.
- egyik sincs a szélén: van két KPK blokk, és a többi golyó fehér, ez 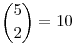 eset (összevonjuk a PKP hármast egyetlen golyóvá, és annak határozzuk meg a helyét). eset (összevonjuk a PKP hármast egyetlen golyóvá, és annak határozzuk meg a helyét).
Ez összesen 20+20+60+10+10+20+10+20+20+10=200 lehetőség. Ha valaki tud lényegesen egyszerűbbet, szóljon :-)
|
| Előzmény: [901] Valvehead, 2009-04-06 09:44:30 |
|
| [901] Valvehead | 2009-04-06 09:44:30 |
 Hányféleképpen lehet 2 piros, 3 fehér és 4 kék golyót egy sorban úgy elhelyezni, hogy piros golyó ne kerüljön fehér golyó mellé?
200 a hivatalos megoldás, de nekem sehogy sem 200 jön ki :( Help!
|
|
| [900] forex | 2009-04-03 18:38:59 |
 Üdvözlök mindenkit!
egy megoldás:
|
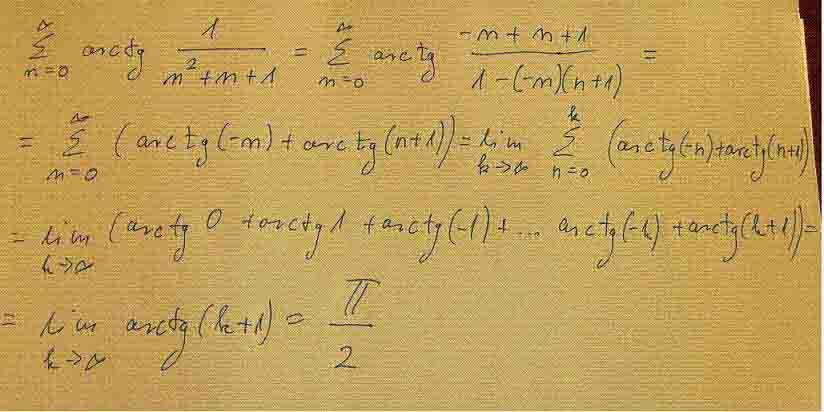 |
|
| [899] Euler | 2009-04-02 22:32:51 |
 Sziasztok! Bizonyitsd be teljes indukcióval, hogy az (n+1)-edik részletösszeg arctg(n+1)-gyel egyezik meg, ezt könnyű belátni, ha használod az arctgx+arctgy=arctg(x+y)/(1-xy) összefüggést, mely az adott intervallumon fennáll. Innen már könnyen be lehet fejezni. Remélem érthetően mondtam el.
|
| Előzmény: [893] Cokee, 2009-04-01 20:12:33 |
|
|
|
|