KöMaL Problems in Mathematics, January 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2014. |
K. 403. How many digits of 8 are there in the decimal form of the sum ?
(6 pont)
solution (in Hungarian), statistics
K. 404. What is the largest three-digit number that is divisible by the product of its digits?
(6 pont)
solution (in Hungarian), statistics
K. 405. a) Find all sets of three integers such that their product is a positive prime and, if they are listed in increasing order, the differences of consecutive numbers are the same?
b) Find all sets of three integers such that their product is the double of a positive prime and, if they are listed in increasing order, the differences of consecutive numbers are the same?
(6 pont)
solution (in Hungarian), statistics
K. 406. We say that an integer is a ``mountain number'' if it consists of digits distinct from one another and from 0, and its digits are increasing from the first one to the ``mountain top'', then decreasing from the top to the last digit. The mountain top cannot be the first or the last digit.
a) Determine the largest and the smallest mountain numbers.
b) How many mountain numbers with 4 digits are there?
(6 pont)
solution (in Hungarian), statistics
K. 407. n and n+200 are perfect squares, and n+100 is 1 greater than a square number. What may be the natural number n?
(6 pont)
solution (in Hungarian), statistics
K. 408. Show that if x, y and z are rational numbers such that x+y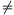 z, z
z, z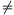 0, and (a-1)2x+(a-1)2y-(a2-1)z=0, then a is also a rational number.
0, and (a-1)2x+(a-1)2y-(a2-1)z=0, then a is also a rational number.
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2014. |
C. 1203. Show that if x, y and z are rational numbers such that x+y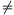 z, z
z, z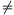 0, and (a-1)2x+(a-1)2y-(a2-1)z=0, then a is also a rational number.
0, and (a-1)2x+(a-1)2y-(a2-1)z=0, then a is also a rational number.
(5 pont)
solution (in Hungarian), statistics
C. 1204. The midpoints of the sides of the convex quadrilaterals ABCD and EFGH coincide. Prove that the two quadrilaterals have equal areas.
(5 pont)
solution (in Hungarian), statistics
C. 1205. Find all right-angled triangles in which the measures of the sides are two-digit integers, the length of the hypotenuse is obtained by interchanging the digits of one leg, and the three two-digit numbers consist of exactly three kinds of digits, each occurring twice.
(5 pont)
solution (in Hungarian), statistics
C. 1206. Five dice are rolled simultaneously. What is the probability that at least two identical numbers are rolled?
(5 pont)
solution (in Hungarian), statistics
C. 1207. E, F and G are points on each side of triangle ABC and n is a natural number such that ,
, and
. Show that if n
 5 then the area of triangle EFG is greater than the half of the area of triangle ABC.
5 then the area of triangle EFG is greater than the half of the area of triangle ABC.
(5 pont)
solution (in Hungarian), statistics
C. 1208. The vertices of the parallelograms PQRL and LSTA in the plane are labelled in the same sense around the clock. The parallelograms do not have a point in common, except L. Prove that there exists a pentagon ABCDE (degenerated cases are allowed) in the plane such that the midpoints of the sides are P, Q, R, S, T, in this order.
(5 pont)
solution (in Hungarian), statistics
C. 1209. The tangents drawn from a point C lying outside a circle touch the circle at points A és B. M is a point on the shorter arc AB. Let MN, ME and MD be the line segments drawn from M, perpendicular to the line segments AB, BC and CA, respectively. Given that MN=4, MD=2 and , find the area of triangle MNE.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2014. |
B. 4592. What may be the number of people in a company in which every member has exactly three acquaintances, and any two people have an acquaintance in common exactly if the two of them do not know each other?
(5 pont)
solution (in Hungarian), statistics
B. 4593. An ant starts crawling at constant speed from the left end of a 4-metre-long rubber rope towards the right end. It covers exactly one metre per minute. The rope is fixed at the left end, in a horizontal position. At the end of each minute, the rope is stretched uniformly by one metre. In which minute will the ant reach the right end of the rope? The ant is considered pointlike, the act of stretching takes negligible time, and the rope can be stretched to any length without breaking it.
(3 pont)
solution (in Hungarian), statistics
B. 4594. Consider a sequence of reflections in the lines of all four sides of a square in some order. How many different transformations are obtained by the composition of four such reflections?
(3 pont)
solution (in Hungarian), statistics
B. 4595. Let d(n) denote the number of positive divisors of a positive integer n. Solve the equation d(n3)=n.
Suggested by Di M. Giovanni, Győr
(5 pont)
solution (in Hungarian), statistics
B. 4596. Solve the equation .
(5 pont)
solution (in Hungarian), statistics
B. 4597. The radii of the escribed circles of a triangle are ra, rb and rc, the radius of the circumscribed circle is R. Determine the angles of the triangle if ra+rb=3R and rb+rc=2R.
Suggested by S. Kiss, Szatmárnémeti
(4 pont)
solution (in Hungarian), statistics
B. 4598. The diagonals of a cyclic quadrilateral ABCD intersect at E, the midpoints of sides AB and CD are K and M, and the perpendicular projections of point E on the sides BC and AD are L and N, respectively. Prove that the lines KM and LN are perpendicular to each other.
(Kvant)
(5 pont)
solution (in Hungarian), statistics
B. 4599. Solve the equation sin5x+cos5x+sin4x=2.
(4 pont)
solution (in Hungarian), statistics
B. 4600. Is it possible to divide the first n prime numbers into two sets such that the sum of elements in each set is the same if
a) n=20132014;
b) n=20142013?
(6 pont)
solution (in Hungarian), statistics
B. 4601. One face of a tetrahedron is a regular triangle of unit side. The length of the other three edges is a. What is the maximum possible area of the perpendicular projection of the tetrahedron on a plane?
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2014. |
A. 605. Let k, m and n be positive integers with m n, and let
n, and let be real numbers. Prove that
Proposed by: Péter Erben and János Pataki, Budapest
(5 pont)
solution (in Hungarian), statistics
A. 606. Prove that for every simple graph G with n vertices there exist some simple graphs S1, ..., Sk with the following properties:
(a) every Si is a complete bipartite graph;
(b) every edge of G is contained by an odd number of graphs Si;
(c) every edge of the complement of G is contained by an even number of graphs Si;
(d) .
(5 pont)
solution (in Hungarian), statistics
A. 607. The circles k1, k2 and k3 are pairwise externally tangent to each other; the point of tangency between k1 and k2 is T. One of the external common tangents of k1 and k2 meets k3 at points P and Q. Prove that the internal common tangent of k1 and k2 bisects the arc PQ of k3 which is closer to T.
(5 pont)
Upload your solutions above.
