A KöMaL 2006. decemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2007. január 10-én LEJÁRT. |
K. 103. András, Béla, Csaba és Dénes kártyáznak. Egy játszmában a négy fiú közül csak három játszik, és a játszma eredményétől függően egymástól nyerhetnek pontokat: vagy egyvalaki a másik kettőtől, vagy ketten a harmadiktól. (Ha két vesztes vagy két nyertes van, akkor ezek nem feltétlenül ugyanannyit nyernek, illetve vesztenek.) A játék kezdetén mindenkinek 100 pontja volt. A fiúk négy játszmát játszottak, mindegyikben más-más maradt ki. Az egyes résztvevők pontjainak alakulását egy táblázatban rögzítették.
|
Melyik játszmában melyik fiú maradt ki?
(6 pont)
K. 104. Háromféle dobozunk van: kicsi, közepes és nagy (az azonos méretű dobozok nem rakhatók egymásba). Kitettünk 11 nagy dobozt az asztalra, majd néhányat ezek közül üresen hagytunk, a többibe pedig 8-8 közepes dobozt tettünk. A közepes dobozok közül is üresen hagytunk néhányat, a többi mindegyikébe pedig 8 (üres) kis dobozt tettünk. Így most 102 üres doboz van az asztalon. Hány doboz van összesen az asztalon?
(6 pont)
K. 105. Egy énekeskönyvben 700 ének van, 1-től 700-ig sorszámozva. Minden vasárnap ebből énekelnek egyet, melynek sorszámát kis fakockákból összerakva jelölik ki. (Az egyjegyű és kétjegyű sorszámokat 0-val kezdve rakják ki, pl. a 3-at 003, a 28-at 028 alakban.) A fakockák oldalain egy-egy számjegy van, és a 6-ost 9-esnek is fel lehet használni.
a) Hány fakockát kell készíteni, hogy minden lehetséges sorszámot ki lehessen rakni? Tervezzünk is meg egy ilyen készletet.
b) Hány éneket vehetnénk még bele az énekeskönyvbe, anélkül, hogy újabb kockát kelljen készítenünk?
(6 pont)
K. 106. Három egymást követő páratlan természetes szám négyzetének összege olyan négyjegyű szám, melynek minden számjegye azonos. Adjuk meg az összes ilyen számhármast. Találunk-e öt egymást követő páratlan természetes számot, melyek négyzetének összege olyan hatjegyű szám, melynek minden számjegye azonos?
(6 pont)
K. 107. Ha az 1234 négyjegyű számból minden lehetséges módon törlünk két számjegyet, majd az így megmaradt két számjegyet kétjegyű számként kiolvassuk, akkor a 12, 13, 14, 23, 24, 34 számokat kapjuk. Ezek összege 120. Keressünk olyan négyjegyű számot, amelynél ez az összeg
a) 540;
b) 220.
(6 pont)
K. 108. Egy 100 m oldalhosszúságú, négyzet alakú füvesített teret a határvonala mentén kövezett járda vesz körbe. Az emberek leggyakrabban a négyzet alakú terület A sarkától a szemközti oldal F felezőpontjába szeretnének eljutni. Ezt úgy is megtehetik, hogy a terület határa mentén a kövezett járdán közlekednek az ABF útvonalon, de néhányan gyalogutat alakítottak ki a füvön keresztül úgy, hogy elindultak az AB oldal mentén, majd egyenesen átvágtak a téren F felé, az ábrán látható módon. Így a határ mentén megtett úthoz képest 25%-kal kevesebb utat kell megtenniük. Milyen messze van az A ponttól a füvön keresztül vezető gyalogút K kezdőpontja?
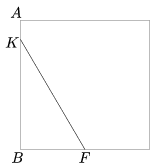
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2007. január 15-én LEJÁRT. |
C. 875. Egy zsömle ára 15 Ft, egy kiflié 12 Ft. Mindkettőből vásárolunk valamennyit.
a) Fizethetünk-e 500 Ft-ot?
b) Fizethetünk-e 600 Ft-ot?
(5 pont)
C. 876. Oldjuk meg a következő egyenletrendszert:
x+y=x2+2xy+y2,
x-y=x2-2xy+y2.
(5 pont)
C. 877. Egy téglalap alakú lapot kettéhajtottunk az átlója mentén úgy, hogy a négy csúcs egy olyan húrtrapézt határoz meg, amelynek három oldala egyenlő, a negyedik oldal hossza pedig . Mekkorák az eredeti téglalap oldalai?
(5 pont)
C. 878. Egy szabályos négyoldalú gúla magassága kétszerese az alapél hosszának. Hányadrésze a gúlába beírt kocka térfogata a gúla térfogatának? (A beírt kocka négy csúcsa a gúla oldalélein, négy csúcsa az alaplapon van.)
(5 pont)
C. 879. 5000 forinttal a zsebünkben elindulunk ajándékokat vásárolni. Három üzletbe térünk be. Mindegyik üzletben megtetszik egy ajándéktárgy, amelyet meg is veszünk, ha futja pénzünkből. Az áruk egymástól függetlenül mindhárom üzletben valószínűséggel 1000, 1500 vagy 2000 Ft. Mekkora az esélye annak, hogy három ajándéktárgyat sikerül vásárolnunk és még pénzünk is marad?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
B. 3952. A Mikulás puttonyokba rakja a szaloncukrokat, mindegyikbe 35-öt. Így a végén 7 szaloncukor megmarad. Mennyi maradna meg, ha csak 15-öt rakna egy csomagba?
(3 pont)
B. 3953. Adott 100 valós szám, az összegük nulla. Legalább hány olyan pár választható ki közülük, amelyben a számok összege nemnegatív?
(5 pont)
B. 3954. Oldjuk meg az alábbi egyenletrendszert:
Forrás: Oláh György: Határon túli matematika versenyek
(4 pont)
B. 3955. Egy színház Lear király előadásán a II.-V. felvonás helyszínét a felvonások előtt sorsolják ki. A nézőtér négy részre oszlik, a nézők a székükkel együtt átülnek egy másik területre, ha éppen az a rész a következő helyszín, ahol ők ülnek. Tegyük fel, hogy mind a négy terület elég nagy ahhoz, hogy ha kiválasztjuk az egyiket, akkor oda le is tudjuk tenni a székünket, és minden területet egyenlő eséllyel választunk ki magunknak. Hányszor akkora annak a valószínűsége, hogy kétszer kell ,,költöznünk'', mint annak, hogy csak egyszer?
(4 pont)
B. 3956. Adott 2006 pont a síkon. Legfeljebb hány olyan pont lehet köztük, amely bármely másik két ponttal hegyesszögű háromszöget határoz meg?
(4 pont)
B. 3957. Az ABC háromszög AB oldalának egy belső pontja D. Az ABC háromszög beírt köre az AB oldalt a P pontban érinti, az ADC és a DBC háromszögek beírt körei Q-ban, illetve R-ben érintik a DC oldalt.
Mutassuk meg, hogy DP=QR.
(3 pont)
B. 3958. Az ABC háromszögnek C-nél derékszöge van, a beírt körének a középpontja O. Az O pontban az OA és az OB szakaszokra bocsátott merőlegesek az AB oldalt P-ben, illetve Q-ban metszik. A P pont merőleges vetülete a BC oldalon P', Q merőleges vetülete az AC oldalon Q'.
Bizonyítsuk be, hogy a P', Q' és O pontok egy egyenesen vannak.
(4 pont)
B. 3959. Jelölje K az A1A2A3 háromszög tetszőleges belső pontját. Legyen Si (i=1,2,3) a KAjAk háromszög súlypontja. Bizonyítsuk be, hogy az AiSi szakaszok egy ponton haladnak át.
(4 pont)
B. 3960. Állítsunk merőlegeseket egy hiperbola valós tengelyére annak két végpontjában. Ezeknek egy tetszőleges érintővel való metszéspontjait jelöljük P-vel és Q-val.
Igazoljuk, hogy a PQ szakasz a fókuszokból derékszögben látszik.
Javasolta: Vajda István (Budapest)
(5 pont)
B. 3961. Legyenek a és b olyan pozitív egész számok, hogy minden n pozitív egész számra an+n osztója bn+n-nek. Igazoljuk, hogy a=b.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2007. január 15-én LEJÁRT. |
A. 413. Legyen O az ABCD konvex négyszög AC és BD átlóinak metszéspontja. Az OAB és OCD háromszögek súlypontja legyen G1, illetve G2. Az OBC és ODA háromszögek magasságpontja legyen H1, illetve H2. Bizonyítsuk be, hogy G1G2 merőleges H1H2-re.
Vietnami versenyfeladat
(5 pont)
A. 414. Igazoljuk, hogy tetszőleges x, y, z pozitív számokra
Iráni versenyfeladat
(5 pont)
A. 415. Bizonyítsuk be, hogy tetszőleges a>b és n pozitív egészek esetén  (an-bn) osztható n-nel. (
(an-bn) osztható n-nel. ( (m) jelöli az m-nél nem nagyobb, m-mel relatív prím pozitív egészek számát.)
(m) jelöli az m-nél nem nagyobb, m-mel relatív prím pozitív egészek számát.)
Javasolta: Strenner Balázs (Budapest)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

