A KöMaL 2008. októberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2008. november 10-én LEJÁRT. |
K. 175. Az ábrán lévő nyolc körbe írjuk be az egész számokat 1-től 8-ig úgy, hogy egyik szám se legyen összeköttetésben nála eggyel kisebbel vagy nagyobbal (pl. a 4 ne legyen összeköttetésben se a 3-mal, se az 5-tel). Adjuk meg az összes különböző megoldást. A megoldás(ok) elkészítésekor számít, hogy melyik betűjelű karikába melyik szám kerül.
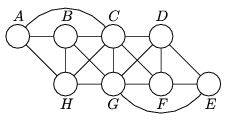
(6 pont)
K. 176. Sanyi a Bloxorz nevű játékot játssza. Ennek az a lényege, hogy egy egységnyi oldalú négyzetekből álló négyzetrácsra rajzolt pályán kell egy egységnyi négyzet alapú, két egységnyi magas hasábot görgetni. A hasáb a pályán mindig egy vagy két négyzeten áll, illetve fekszik, és megengedett lépés, hogy a hasábot valamelyik éle mentén átfordítjuk úgy, hogy az eddig alul levő lapjával szomszédos lapján fog állni, illetve feküdni. (A megengedett mozgásokat az ábra szemlélteti.)
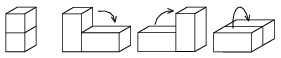
A játék során a hasáb nem mehet le a pályáról, azaz nem állhat vagy fekhet még részlegesen sem olyan területen, mely a pályán kívül van. A játék célja, hogy egy adott kezdőpozícióból indulva a hasábot úgy kell mozgatni, hogy az az X-szel jelzett mezőn álljon (vagyis a hasáb a pályának csak ezzel a mezőjével érintkezzen). (A játék internetes változata a http://miniclip.com/games/bloxorz/en címen található meg.)
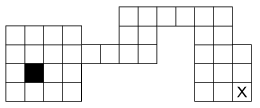
Az ábra mutatja a pályát. A hasáb kezdetben a feketével jelölt területen áll. Juttassuk el a hasábot az X-szel jelölt mezőre, álló helyzetbe. Rajzoljuk le a hasáb egymás utáni helyzeteit (számokkal jelölve a sorrendet), melyeken keresztül az X-szel jelzett mezőre eljut. Mindaddig használjuk ugyanazt az ábrát, amíg a soron következő helyzet nem fed le valamelyik korábbi helyzethez tartozó négyzetet a táblán. Ilyenkor rajzoljunk új ábrát, és azon jelöljük folytatólagosan a további helyzeteket. Adjunk olyan megoldást, ami 30-nál kevesebb lépésből áll.
(6 pont)
K. 177. Hogyan kell hat szomszédos természetes számot megválasztanunk, hogy a négyzetük összege osztható legyen 7-tel?
(6 pont)
K. 178. Egy számsorozatban a második számtól kezdve bármelyik számot megkaphatjuk úgy, hogy a sorszámához hozzáadjuk a sorozatban közvetlenül előtte álló szám reciprokát. A sorozatban az ötödik szám . Határozzuk meg a sorozatban álló negyedik és hatodik számot.
(6 pont)
K. 179. Jancsi egy kördiagramon ábrázolta, hogy mire költötte októberi zsebpénzét. 1500 Ft-ot költött tízóraira, 1000 Ft-ot eltett ajándékok vásárlására, 1250 Ft-ot költött mozijegyre, 500 Ft-ot pedig DVD-filmek kölcsönzésére. A kördiagramon a rágóra költött pénzét egy 20 fokos körcikk jelenítette meg. Az említetteken kívül októberben más kiadása nem volt. Hány forintot költött Jancsi októberben rágóra?
(6 pont)
K. 180. Beírjuk 1-9-ig az egész számokat egy 3×3-as táblázatba valamilyen sorrendben, majd az egyes oszlopokban, illetve sorokban álló számjegyek balról jobbra, illetve fentről lefelé történő összeolvasásával kapott hat számot összeadjuk. Mennyi az így kapható két legkisebb lehetséges összeg? Például az ábrán látható elrendezésben az említett módon kiszámított összeg 531+296+748+527+394+168=2664.
|
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2008. november 17-én LEJÁRT. |
C. 955. Oldjuk meg a 10x-5=9[x] egyenletet a valós számok halmazán (ahol [x] az x egész részét jelenti).
(5 pont)
C. 956. Egy sokszög oldalainak számát megkétszerezzük. Melyek azok a sokszögek, amelyek esetén az új sokszög szögeinek összege egész számú többszöröse az eredeti sokszög szögösszegének?
(5 pont)
C. 957. Egy téglalap oldalai a és b. A téglalapban két egybevágó kört helyezünk el úgy, hogy nincs közös belső pontjuk. Mekkora a téglalap oldalainak aránya, ha a legnagyobb ilyen körök átmérője:
(5 pont)
C. 958. Egy társasjátékban, amelyet dobókockával játszunk, bábunk négy mezőnyire van a céltól. Ha legalább négyet dobunk, akkor célba értünk. Ha hármast dobunk, akkor a következő dobással biztosan benn vagyunk.
Mennyi annak a valószínűsége, hogy csak kettőnél több dobással jutunk célba?
(5 pont)
C. 959. Egy csonkakúp egyik alapkörének átmérője 100 mm. Ha az átmérőt 21%-kal növeljük, miközben a magasság és a másik alapkör mérete nem változik, a csonkakúp térfogata ugyancsak 21%-kal nő. Mekkora a másik alapkör átmérője?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2008. november 17-én LEJÁRT. |
B. 4112. Egy téglalap alakú ABCD biliárdasztal A csúcsából a szögfelező irányában ellökünk egy golyót, mely a CD, BC majd AB oldalakról visszapattanva éppen telibe találja a téglalap közepén álló golyót. Milyen más irányban lökhetjük még el a golyót az A pontból, hogy három különböző oldalról visszapattanva szintén telibe találja a középen álló golyót?
(4 pont)
B. 4113. Bizonyítsuk be, hogy ha a, b, c, d egészek és a+b+c+d=0, akkor 2(a4+b4+c4+d4)+8abcd négyzetszám.
(4 pont)
B. 4114. Egy 11-szer 7-es téglalapból négy egybevágó négyzetet kivágtunk az ábrán látható módon.
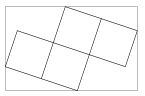
A téglalap hány százaléka hulladék?
(3 pont)
B. 4115. Mely k pozitív egész esetén fordul elő az 1 az (an) sorozat elemei között, ha a1=k, és , ha an páros, illetve an+1=an+5, ha an páratlan?
(5 pont)
B. 4116. Oldjuk meg minden n pozitív egész szám esetén a
cosnx-sinnx=1
egyenletet.
(4 pont)
B. 4117. Egy P pontra illeszkedő három egyenest további kettő rendre az A, B, C és az A', B', C' pontokban metsz. Bizonyítsuk be, hogy
ahol a hányadosok előjelesen értendők.
(5 pont)
B. 4118. Felbontható-e a zárt körlap két diszjunkt, egybevágó ponthalmaz egyesítésére? (A zárt körlap a körvonal pontjait is tartalmazza.)
(5 pont)
B. 4119. Igazoljuk, hogy az
függvény grafikonja szimmetrikus a (-4;3) pontra.
Kiss Sándor (Szatmárnémeti) javaslata alapján
(3 pont)
B. 4120. A véges sok egybevágó zárt körlap metszeteként előálló alakzatokat nevezzük levélnek, ezeknek valamely definiáló körlap határával vett metszetét a levél oldalának. Bizonyítsuk be, hogy a levelek oldalai összefüggők.
(4 pont)
B. 4121. Egy csomag francia kártyából addig húzzuk a lapokat egyesével, amíg póker nem lesz a kezünkben. Az első kihúzott lap ász. Mi annak a valószínűsége, hogy ász pókernél állunk meg?
Javasolta: Maga Péter
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2008. december 15-én LEJÁRT. |
A. 461. Az ABCD tetraéder ABC lapjához hozzáírt gömb az ABC lapot a P pontban, az ABD laphoz hozzáírt gömb pedig az ABD lapot Q-ban érinti. Igazoljuk, hogy .
(5 pont)
A. 462. Legyen p páratlan prímszám és 1<a<p egész. Bizonyítsuk be, hogy
akkor és csak akkor osztható p-vel, ha létezik olyan páratlan k pozitív egész, amelyre az ak szám 1 maradékot ad p-vel osztva.
(5 pont)
A. 463. Legyenek a1<a2<...<an és b1<b2<...<bn valós számok. Mutassuk meg, hogy
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

