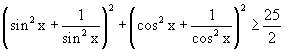| [36] Geg | 2006-01-09 14:45:59 |
 A henger egyes retegeiben lokalis termodinamikai egyensuly van, ezert egy-egy ilyen vekony savban ervenyes az allapotegyenlet. Fel kell irni a Newton egyenletet egy ilyen kis retegre: felette es alatta levo gaz nyomasabol szarmazo ero + a sajat sulya. Ebben megjelenik a lokalisan jelen levo suruseg, amit az allapotegyenlettel at lehet jatszani nyomasra, igy kapunk egy differencialegyenletet, de abban szerepel meg a homerseklet is, mint a magassag fuggvenye. Ezt a hovezetes egyenletebol lehet meghatarozni. Mivel az allapot stacionarius, ezert a hovezetes egyenlete miatt a homerseklet magassag szerinti masodik derivaltja nulla (itt feltettuk, hogy a hovezetesi tenyezo nem fugg a helytol), vagyis a fv linearis, es tudnia kell, hogy fent 380K, alul pedig 200K a homerseklet. A nyomasra vonatkozo differencialegyenlet most mar megoldhato, amit az allapotegyenlettel vissza lehet jatszani surusegre. Ha a suruseg ismert a magassag fuggvenyeben, akkor a tomegkozeppont egyszeru integralassal adodik.
|
| Előzmény: [35] !X!, 2006-01-09 10:08:45 |
|
| [35] !X! | 2006-01-09 10:08:45 |
 Sziasztok!!!
Nagyon hálás lennék, ha valaki segítene megoldani ezt a feladatot:
Egy h magasságú, A alapterületű hengeralakú edényben levegő van. Az edény alját 200 K hőmérsékleten, a tetejét pedig 380 K-en tartjuk. Határozzuk meg a tömegközéppont helyzetét!
|
|
| [34] Nandi001 | 2005-12-30 19:00:31 |
 szia lorantfy!
köszi a gyors választ!!!sokat segítettél. igy már nagyon egyszerű, csak nem értettem a jelöléseket.
|
|
| [33] lorantfy | 2005-12-30 18:01:18 |
 Szia Nandi!
f(x,y)=3x2y+2xy2 Ez egy kétváltozós fgv., x és y a két változó. Lehet x szerint és y szerint deriválni és a kapott derivált fgv-eket lehet újra deriválni x és y szerint. Ezek a fgv elsőrendű és másodrendű parciális deriváltjai. Sokféle jelölés van forgalomban.
[fx(x,y)]' az x szerinti első derivált. Ezt úgy kapod, hogy x szerint deriválod a fgv-t miközben a y-t konstansnak tekinted. Az első tagban x2 deriváltja 2x és ezt szorzod 3y-nal. A másodikban 2x-nek pedig 2, szorozva y2-tel így:
[fx(x,y)]'=6xy+2y2
Hasonlóan ha y szerinti deriválsz, akkor az x-et tekinted konstansnak. Igy az y szerinti első derivált: az első tagban 3y-nak 3 és marad az x2 szorzó, a második tagban y2-nek 2y a deriváltja, szorozva 2x-el.
[fy(x,y)]'=3x2+4xy
[fxy(x,y)]'' : ez a másodrendű vegyes parciális derivált. Ezt úgy kapod, hogy az x-szerinti első deriváltat most y szerint deriválod úgy, hogy közben az x-et konstansnak tekinted.
[fxy(x,y)]''=6x+4y
[fyx(x,y)]'' : ez is a másodrendű vegyes parciális derivált, csak a sorrend más. Ezt úgy kapod, hogy az y-szerinti első deriváltat x szerint deriválod úgy, hogy közben az y-t konstansnak tekinted.
[fyx(x,y)]''=6x+4y
Itt ugyanazt kell kapni mint az előbb, szóval nem függ a sorrendtől.
Aztán szokták még kérdezni a az x szerinti második és az y szerinti második deriváltakat.
[fxx(x,y)]'' és [fyy(x,y)]''
Ezeket értelem szerűen úgy kapod, hogy az x szerinti első deriváltat újra x szerint deriválod, illetve az y szerinti elsőt újra y szerint.
[fxx(x,y)]''=6y és [fyy(x,y)]''=4x
|
| Előzmény: [32] Nandi001, 2005-12-30 13:40:23 |
|
| [32] Nandi001 | 2005-12-30 13:40:23 |
 hali!
van egy feladatom nem tudok mit kezdeni vele.
f(xy)=3yxx+2xyy ezt kellene deriválni
[fx(xy)]'=? [fy(xy)]'=? [fxy(xy)]'=? [fyx(xy)]'=?
lehet hogy egyszerű, de nem értem ezeket a jelöléseket. Előre is kössz a választ!
|
|
|
|
| [29] Suhanc | 2005-12-23 15:14:56 |
 Kedves Fórumososok!
Bevallom őszintén, nem olvastam el, eddig milyen kérdések adódtak ebben a topicban, de a címe alapján remélem helyénvaló, hogy itt kérjek segítséget:
Ha valaki ismeri a nevezetes (számtani, mértani, harmonikus, négyzetes) közepek elnevezését (esetleg jelölését) angolul, kérem, írja be ide!
Előre is köszönöm a segítséget!
|
|
|
|
| [26] Kriván Bálint | 2005-12-07 08:52:40 |
 Üdv! Nem tudnátok mondani egy olyan oldalt (honlapot), ahol meg lehet tanulni deriválni? (kéne egy függvény szélső értékei...)
Köszi!
|
|
| [25] philip | 2005-12-05 16:52:22 |
 Én még csak tizedikes vagyok,és most a trigonometria kapcsán kaptuk ezt a szorgalmi feladatot.....
|
|
|
| [23] qer | 2005-12-04 18:29:53 |
 Elnézést mindenkitől, csak amikor megoldok egy feladatot, akkor nem szoktam magamnak magyarázatot fűzni hozzá, így már megszoktam ezt a fajta írást mindenféle megjegyzés nélkül... pótolnám hiányosságom (számozás fentről lefelé) (1) a kiinduló egyenlőtlenség, mivel a négyzetekről beugrott a négyzetes és a számtani közép közti egyenlőtlenség, az (1) bal oldalát úgy alakítgattam, azaz osztottam 2-vel (majd mivel nemnegatív az érték) négyzetgyököt vontam, így lett a (2).A (3) a már emlegetett négyzetes-számtani egyenlőtlenség felírása. Nyílván ha a kisebb (azaz a számtani közép) is nagyobb mint 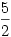 , akkor a négyzetes is. Ezért folytattam a számtani középre a bizonyítást , így lett a(4). Ezután már egyszerű átalakítgatások (ezek már könnyűek nem részletezném), majd egyetlen egy észrevétel hogy 4sin2xcos2x=sin22x. A szinusz fv. jól ismert tulajdonságai miatt az utolsó egyenlőtlenség teljesül, emiatt az előzőek is. , akkor a négyzetes is. Ezért folytattam a számtani középre a bizonyítást , így lett a(4). Ezután már egyszerű átalakítgatások (ezek már könnyűek nem részletezném), majd egyetlen egy észrevétel hogy 4sin2xcos2x=sin22x. A szinusz fv. jól ismert tulajdonságai miatt az utolsó egyenlőtlenség teljesül, emiatt az előzőek is.
|
|
| [22] Lóczi Lajos | 2005-12-04 16:42:28 |
 Akkor lenne igazán jó és érthető a leírás, ha nem csak egymás alá lennének írva a sorok, hanem oda lenne írva, hogy egyik sor egyenértékű-e a másikkal, vagy csak egy alsó sor elégséges feltétele-e a felsőnek. Nyilván erre gondoltál, de a logikai váz éppoly fontos, mint a formulák.
|
| Előzmény: [17] qer, 2005-12-04 12:37:13 |
|
|
| [20] philip | 2005-12-04 15:51:35 |
 Én a 3. sort nem vágom.....Magyarázza el valaki lécci!
|
|
|
|
|
| [16] philip | 2005-12-04 09:18:54 |
 Erre valaki tud valami okosat mondani...nagyon megköszönném!
|
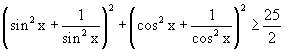 |
|
| [15] Lóczi Lajos | 2005-11-22 14:32:09 |
 Olyan formában nem, ahogy írtad, de ha valamelyik tényező egy derivált, akkor igen, pl. n=3-ra:
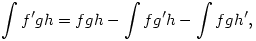
ami persze csak a szorzat deriválási szabálya 3-tényezős szorzatokra.
|
| Előzmény: [14] Wolf, 2005-11-22 12:25:18 |
|
| [14] Wolf | 2005-11-22 12:25:18 |
 Mikor még tanultuk a parciális integrálást, két függvény szorzatát bontottuk fel, de létezik-e több fv szorzatára ilyen módszer?
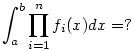
Köszönöm
|
|
|
| [12] Lóczi Lajos | 2005-11-22 01:06:42 |
 Persze, hogy létezik a limsup, de a limesz létét is el lehet érni, és egy limeszt könnyebb "látni". Az én példámban a teljes tér a [0,1] intervallum volt (nem volt feltétel, hogy az egész számegyenes legyen).
Bár egyik példa sem ad választ az eredeti kérdésre: ő megszámlálhatóan végtelen sok értékre kérdezett rá :)
|
| Előzmény: [11] Róbert Gida, 2005-11-21 23:53:20 |
|








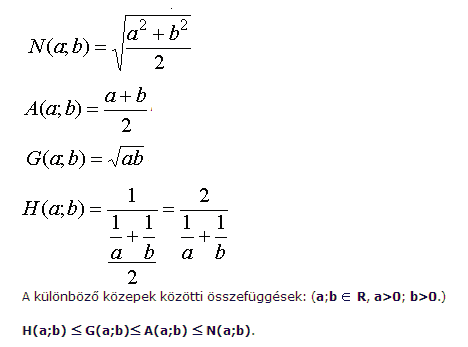
 4sin2xcos2x
4sin2xcos2x