A KöMaL 2019. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2019. február 11-én LEJÁRT. |
M. 383. Mérjük meg, hogy mennyi idő alatt pereg le egy lejtőn álló homokóra a lejtő hajlásszögének függvényében!
Közli: Nagy Piroska Mária, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2019. február 11-én LEJÁRT. |
G. 657. Egy tető nélküli, négyzet alapú, egyenes hasáb alakú akvárium alját 1 cm vastagságú, négyzet alakú üveglapból készítjük. Az oldallapok szintén ugyanilyen vastag üvegből készülnek. Az akvárium belső magassága 20 cm, aljának belső mérete \(\displaystyle 30\times 30\) cm.
Az elkészült akváriumba vizet töltünk. A csapból másodpercenként 5 cm\(\displaystyle {}^3\) víz jut az akváriumba.
\(\displaystyle a)\) Hány óra múlva telik meg az akvárium fele vízzel?
\(\displaystyle b)\) Mekkora a vízzel félig töltött akvárium súlya?
(A víz sűrűsége 1000 kg/m\(\displaystyle {}^3\), az üveg sűrűsége 2500 kg/m\(\displaystyle {}^3\).)
(3 pont)
G. 658. Egy testre 6 erő hat egyszerre: \(\displaystyle F_1=1\) N, \(\displaystyle F_2=2\) N, \(\displaystyle F_3=3\) N, \(\displaystyle F_4= 4\) N, \(\displaystyle F_5=5\) N és \(\displaystyle F_6=6\) N. Az erők egy síkban vannak, és az egymást követő erők közötti szög \(\displaystyle 60^\circ\) (vagyis az erők egymás utáni elfordulása \(\displaystyle 60^\circ\), mindig ugyanabba a forgásirányba).
\(\displaystyle a)\) Mekkora a 6 erő vektori összege?
\(\displaystyle b)\) Hogyan változtassuk meg az \(\displaystyle F_2\) erő nagyságát és esetleg az irányát is, hogy a test egyensúlyban legyen?
(3 pont)
G. 659. Két 50 W teljesítményű, 230 V-ra tervezett karácsonyfaizzó-füzérünk van. Az egyik füzérben 50, a másikban 100 egyforma izzó van sorba kötve.
\(\displaystyle a)\) Melyik füzérben nagyobb az áramerősség?
\(\displaystyle b)\) Melyikben nagyobb az egyes izzók ellenállása?
\(\displaystyle c)\) Nő vagy csökken a 100 darabos füzér teljesítménye, ha 10 izzóját kicseréljük az 50 darabos füzér 10 izzójára? (Feltételezzük, hogy egyetlen izzó sem ég ki.)
(3 pont)
G. 660. Egy falhoz kötött, vízszintesen kifeszített, rugalmas szalagon egy csiga mászik 1 m/h sebességgel. A csiga a faltól indul, a szalag kezdeti hossza 2 m. Az indulástól számított minden óra végén a szalagot a végénél fogva 1 méterrel megnyújtjuk. Az indulás után mennyi idővel érkezik a csiga a szalag végére?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2019. február 11-én LEJÁRT. |
P. 5089. Az ábrán látható, súrlódásmentes pálya két körívből áll. A pálya \(\displaystyle A\) pontjából nagyon kicsi kezdősebességgel indulva csúszik egy apró test. Mennyi idő alatt jut el a test a görbült pálya jobb oldali végéig (a \(\displaystyle B\) pontig)?
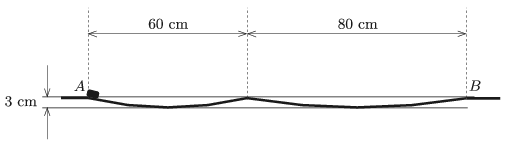
Közli: Simon Péter, Pécs
(4 pont)
P. 5090. Vízszintes talajon egy \(\displaystyle m\) tömegű, kocka alakú doboz áll. A doboz egyik lapjának közepéhez egy ugyancsak \(\displaystyle m\) tömegű, vékony, homogén pálca támaszkodik. Kezdetben mindkét testet rögzítetten tartjuk. A pálca és a talaj által bezárt szög \(\displaystyle \alpha=45^\circ\).
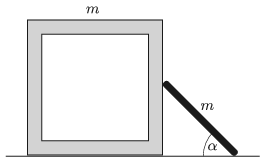
Mekkora gyorsulással indul el a doboz, ha a testeket elengedjük? (A súrlódás mindenhol elhanyagolható.)
Közli: Berke Martin, Zalaegerszeg, Zrínyi Miklós Gimnázium
(5 pont)
P. 5091. A normál állapotú levegő sűrűsége kb. 0,0013 g/cm\(\displaystyle {}^3\), a folyékony levegőé kb. 0,87 g/cm\(\displaystyle {}^3\).
\(\displaystyle a)\) Becsüljük meg, hány ,,levegőmolekula'' található 1 cm\(\displaystyle {}^3\) normál állapotú levegőben, illetve folyékony levegőben!
\(\displaystyle b)\) Becsüljük meg egy ,,levegőmolekula'' tömegét!
Közli: Völgyi István, Budapest
(3 pont)
P. 5092. Vízszintes helyzetű, jól hőszigetelt, rögzített hengert egy \(\displaystyle m\) tömegű, \(\displaystyle A\) keresztmetszetű, könnyen mozgó, rossz hővezető anyagból készült dugattyú két egyenlő, \(\displaystyle V_0\) térfogatú részre oszt. Az egyes részekben azonos mennyiségű, \(\displaystyle p_0\) nyomású héliumgáz van.
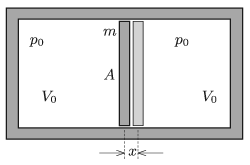
A dugattyút kissé kitérítjük egyensúlyi helyzetéből, majd magára hagyjuk. Mekkora lesz a rezgésidő?
Közli: Németh László, Fonyód
(5 pont)
P. 5093. Egy űrállomáson a súlytalanság állapotában végzett kísérlet kérdése speciális ,,kozmikus sebességgel'' kapcsolatos: Egy \(\displaystyle R=10\) cm sugarú, \(\displaystyle Q=-10^{-7}\) C töltésű, homogén töltéseloszlású szigetelőgömb felületétől \(\displaystyle d=2~\)cm-re mekkora az első és a második kozmikus sebesség egy \(\displaystyle m=0{,}1~\)g tömegű, \(\displaystyle q=2\cdot10^{-9}\) C töltésű, pontszerű testre vonatkozóan?
Közli: Holics László, Budapest
(4 pont)
P. 5094. Három, \(\displaystyle L=20~\)cm hosszúságú szigetelőfonál egyik végéhez \(\displaystyle m=1~\)g tömegű, pontszerűnek tekinthető testeket erősítettek, amelyek töltése (egyenként) \(\displaystyle Q=3{,}1\cdot 10^{-7}\) C. A fonalak másik végét közös pontban rögzítették. Kezdetben a feszes fonalak a függőlegessel \(\displaystyle \alpha=30^\circ\)-os szöget zárnak be, és a kis testek egy szabályos háromszöget alkotnak. Ezt követően egyszerre elengedjük a testeket.
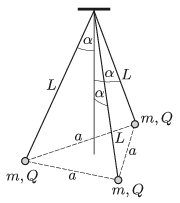
\(\displaystyle a)\) Mekkora szöget zárnak be a fonalak a függőlegessel, amikor a testek sebessége maximális?
\(\displaystyle b)\) Mekkora a testek legnagyobb sebessége?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5095. Sorba kötöttünk \(\displaystyle R_1\) és \(\displaystyle R_2\) ellenállást, az eredőjük \(\displaystyle R_1+R_2\). Ebbe az áramkörbe \(\displaystyle R_1\)-gyel párhuzamosan és \(\displaystyle R_2\)-vel sorosan bekötöttünk egy-egy \(\displaystyle R\) nagyságú ellenállást. Van-e olyan \(\displaystyle R\) érték, amely esetén az eredő ellenállás továbbra is \(\displaystyle R_1+R_2\) marad?
Közli: Kobzos Ferenc, Dunaújváros
(4 pont)
P. 5096. Egy 4 cm sugarú tömör, homogén üveggömb középpontjától 10 cm-re van egy 2 mm sugarú, világító, kicsiny körlap. A körlap síkja merőleges a kör és a gömb középpontját összekötő egyenesre (az optikai tengelyre). Hol keletkezik és mekkora lesz e körlapnak az üveggömb által előállított képe? (Az üveg törésmutatója 1,5, és a képalkotásban csak az optikai tengelyhez közel haladó fénysugarak vesznek részt.)
Közli: Radnai Gyula, Budapest
(5 pont)
P. 5097. Egy átlátszatlan lapon három vékony rés található, a szomszédos rések távolsága \(\displaystyle d\). A középső rés szélessége \(\displaystyle \sqrt{2}\)-ször nagyobb, mint a szélső két rés szélessége. A réseket a lap síkjára merőlegesen \(\displaystyle \lambda\) hullámhosszúságú lézernyalábbal világítjuk meg, a diffrakciós képet az \(\displaystyle L\) távolságra lévő ernyőn észleljük. A nulladrendű maximumtól milyen távolságra van az ernyőn az első nulla intenzitású hely? (Tegyük fel, hogy \(\displaystyle \lambda\ll d\ll L\)!)
Közli: Vigh Máté, Budapest
(5 pont)
P. 5098. A csillagok színképvonalai – többek között – a csillag tengely körüli forgása miatt is kiszélesednek. Egy csillag színképében a hidrogén \(\displaystyle \rm H\delta\)-val jelölt (a Balmer-sorozatba eső), laboratóriumban 410,174 nm hullámhosszúságú vonalát a 410,171 nm és a 410,177 nm közötti tartományra kiszélesedve észleljük.
\(\displaystyle a)\) Mekkora a csillag tengelyforgási periódusa, ha az átmérője \(\displaystyle 1{,}4\cdot 10^9\) m? Tételezzük fel, hogy a csillag forgástengelye merőleges a látóirányunkra, és a vonalkiszélesedést főként a csillag forgása okozza.
\(\displaystyle b)\) Milyen következtetést vonhatnánk le a csillag mozgásáról, ha a vonalat 410,176 nm és 410,182 nm közötti tartományra kiszélesedve észlelnénk?
Közli: Kovács József, Szombathely
(5 pont)
P. 5099. Egy hullámvasút kocsija egy függőleges síkban fekvő, kör alakú pályán halad úgy, hogy a saját motorját és fékjét használva a sebességét állandó értéken tartja. Legalább mekkora sebességet kell tartania ahhoz, hogy az \(\displaystyle R\) sugarú pályán megcsúszás nélkül tudjon végighaladni, ha a tapadó súrlódás együtthatója \(\displaystyle \mu\)? Hol csúszna meg, ha a sebessége ennél kicsit kisebb lenne? A kocsi elég kicsi a pálya sugarához képest.
Közli: Takács László, Baltimore, USA
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

