A KöMaL 2020. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2020. március 10-én LEJÁRT. |
M. 393. Egy sodrott spárgát vagy fonalat függesszünk fel, majd terheljük meg különböző súlyokkal! Kezünkkel folyamatosan fékezve engedjük kitekeredni a szálat egészen addig, amíg egyensúlyi állapotba nem jut. Hogyan függ a szál aljának elfordulása a terheléstől?
Közli: Tichy Géza, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2020. március 10-én LEJÁRT. |
G. 697. Belenézünk egy kaleidoszkópba; a látvány egy részét az ábra mutatja. Hol helyezkedhetnek el a kaleidoszkóp tükrei?
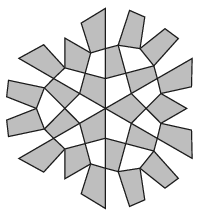
(3 pont)
G. 698. Három tömör kockánk van, amelyek oldalélei 1 cm, 3 cm és 9 cm. Hányszor nagyobb nyomást fejt ki a kockákból épített torony a vízszintes asztallapra, ha a legnagyobb kocka helyett a legkisebbet helyezzük alulra?
(3 pont)
G. 699. Pályaudvarokon, vasútállomásokon figyelhetjük meg, hogy elektromos vezetékeket például az ábrán látható módon csigákon átvetett drótkötélre akasztott, nehéz súlyokkal feszítenek ki.
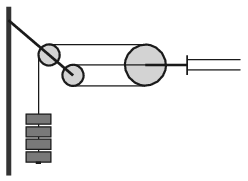
\(\displaystyle a)\) Miért előnyösebb ez a módszer, mintha fix rögzítése lenne a felsővezetéknek?
\(\displaystyle b)\) Mekkora erő feszíti a dupla vezeték egyes szálait, ha a feszítősúlyok együttes tömege 300 kg?
\(\displaystyle c)\) Egy verőfényes, felhőtlen napon hogyan változik a súlyok helyzete reggeltől estig?
(4 pont)
G. 700. A D28 jelű, 315 milliárd tonnás jéghegy (az úgynevezett Zápfoghegy) 2019. szeptember 25-én vált le az Antarktiszról. Ha kis jégkockákká törnénk, és \(\displaystyle 20\;{}^\circ\)C-os vízbe szórnánk, hány Balatonnyi vizet tudna \(\displaystyle 0\;{}^\circ\)C hőmérsékletűre hűteni? A Balaton vizének térfogata 1,9 km\(\displaystyle {}^3\). A jéghegyet tekintsük egységesen \(\displaystyle -10\;{}^\circ\)C hőmérsékletűnek.
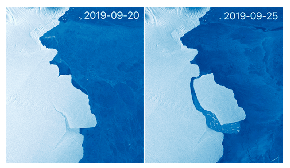
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2020. március 10-én LEJÁRT. |
P. 5197. Micimackó kapott ajándékba egy 20 cm sugarú, gömb alakú lufit. A léggömb úgy volt megtöltve héliummal, hogy ha elengedte a fonalát, éppen lebegett a levegőben, nem emelkedett fel, de nem is süllyedt le.
Micimackó örömében elkezdett körbe szaladni a lufival úgy, hogy az egyik kezével fogta a lufi fonalának végét. Így a lufi egyenletes körmozgást végzett. Malacka megfigyelte, hogy bármekkora is Micimackó állandó szögsebessége, a lufi fonala mindig \(\displaystyle 45^\circ\)-os szöget zár be a kör érintőjével.
Mekkora a lufi körpályájának sugara? (A fonál súlyától és a lufi alakjának esetleges megváltozásától eltekinthetünk.)
Közli: Baranyai Klára, Veresegyház
(5 pont)
P. 5198. Hasáb alakú, \(\displaystyle M\) tömegű test nyugszik egy vízszintes, sima lapon. Egy \(\displaystyle D\) rugóállandójú, a hasáb hossztengelyével párhuzamos, könnyű rugó egyik végét a hasábhoz rögzítjük, a másik végére egy elhanyagolható tömegű ütközőtányért erősítünk. Egy másik, \(\displaystyle m\) tömegű test \(\displaystyle v_0\) sebességgel nekicsúszik a tányérnak úgy, hogy az elegendő hosszúságú rugót részben összenyomja.
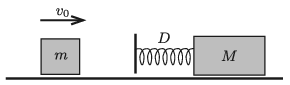
\(\displaystyle a)\) Mekkora a rendszer tömegközéppontjának sebessége?
\(\displaystyle b)\) A \(\displaystyle m\) tömegű test és a tányér érintkezésétől számítva mennyi idő múlva lesz a rugó a legrövidebb?
Közli: Wiedemann László, Budapest
(5 pont)
P. 5199. Az ábrán látható \(\displaystyle \ell\) hosszú, körív alakú, vékony (de kellően merev) fémhuzal mindkét végpontját \(\displaystyle \ell\) hosszúságú, igen könnyű fonállal a körív \(\displaystyle O\) középpontjához erősítjük. Az így elkészített inga az ábra függőleges síkjában \(\displaystyle T_1\) periódusidejű, kis kitérésű lengéseket végezhet az \(\displaystyle O\) pont körül. Ha a fémhuzalt kiegyenesítjük, az így átalakított test az ábra síkjában \(\displaystyle T_2\) periódusidejű, kis kitérésű lengéseket végezhet. Mekkora a \(\displaystyle T_2/T_1\) arány?
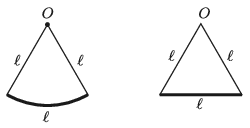
Közli: Simon Péter, Pécs
(5 pont)
P. 5200. Egy völgy felett átívelő függőhídban a transzverzális rezgések mintegy 400 m/s sebességgel terjednek. Egy viharban a hidat érő erős szél másodpercenként ismétlődő erőlökéseket hozott létre. Mekkora lehetett a függőhíd pilléreinek távolsága, ha a híd erős lengésekbe kezdett?
Közli: Radnai Gyula, Budapest
(3 pont)
P. 5201. Az ábrán látható elrendezésben a rugók direkciós ereje \(\displaystyle D= 1000\) N/m, a külső légnyomás \(\displaystyle p_0= 10^5\) Pa, és az \(\displaystyle A=10~{\rm dm}^2\) keresztmetszetű dugattyú által elzárt gáz egyatomos. Kezdetben a rugók nyújtatlanok, ekkor a gáz térfogata \(\displaystyle V_0=50\) liter. Mennyit mozdul el a dugattyú, ha a gázzal \(\displaystyle Q=2~\rm kJ\) hőt közlünk? (A tartály fala és a dugattyú hőszigetelő, a súrlódás és a fűtőszál hőkapacitása elhanyagolható.)
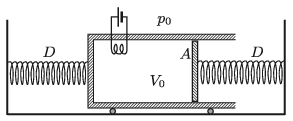
Közli: Berke Martin, Zalaegerszeg, Zrínyi M. Gimnázium
(4 pont)
P. 5202. A fémek fajhője nagyon alacsony hőmérsékleteken jó közelítéssel az abszolút hőmérséklettel arányos (\(\displaystyle c=\alpha \cdot T\), az \(\displaystyle \alpha\) arányossági tényező a fémre jellemző állandó). Egy hidegfizikai laboratórium igen jó hőszigetelésű kamrájában két különböző tömegű és különböző fajta fémet összeérintünk. Az egyik (\(\displaystyle A\) jelű) fémdarab kezdeti hőmérséklete 1,0 K, a (\(\displaystyle B\) jelű) másiké 3,0 K, a kialakuló közös hőmérséklet pedig 2,0 K. Mennyi lesz a közös hőmérséklet, ha a fémdarabok kezdeti hőmérséklete: \(\displaystyle T_A=1{,}5\) K és \(\displaystyle T_B=2{,}5\) K?
Közli: Bertalan Zoltán, Békéscsaba
(5 pont)
P. 5203. Egy \(\displaystyle 2A\) széles, átlátszó üveglemezben a lemez síkjára merőleges \(\displaystyle z\) tengely irányában változik a törésmutató, értéke \(\displaystyle z=\pm A\)-nál \(\displaystyle n_0\), míg \(\displaystyle z=0\)-nál \(\displaystyle n_1\). Az üveglemez szélénél (\(\displaystyle z=A\) ,,magasságban'') az \(\displaystyle x\) tengely irányában egy vékony lézersugarat indítunk, amely az üvegben eltérülve egy koszinuszgörbe mentén halad.
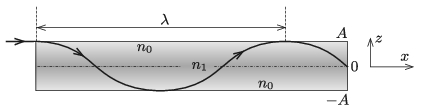
\(\displaystyle a)\) Hogyan függ a törésmutató \(\displaystyle z\)-től?
\(\displaystyle b)\) Mekkora a fény pályagörbéjének hullámhossza?
Adatok: \(\displaystyle A=1\) cm, \(\displaystyle n_0=1{,}5\) és \(\displaystyle n_1=1{,}6\).
(Lásd a P. 5066. feladat megoldását a KöMaL 2018. évi decemberi számában.)
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5204. Határozzuk meg az ábrán vázolt katódsugaras oszcilloszkópcső érzékenységét mm/volt egységben!
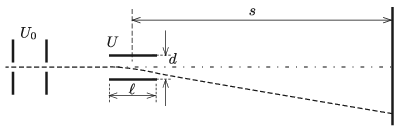
Adatok: az eltérítőlemezek hossza \(\displaystyle \ell=2\) cm, a lemezek távolsága \(\displaystyle d= 0{,}5\) cm, az ernyő távolsága a lemezek közepétől \(\displaystyle s=20\) cm, a gyorsítófeszültség \(\displaystyle U_0=1000\) V, és az eltérítőfeszültség legnagyobb értéke \(\displaystyle U_\text{max}=100\) V.
Közli: Holics László, Budapest
(4 pont)
P. 5205. Az ábra rézvezetékből készült hurkot mutat, amely két koncentrikus félkörből és az azokat összekötő egyenes vezetékekből áll. A hurok vízszintes asztalon fekszik, először a kisebbik félkör függőleges helyzetben van. A kisebbik félkör a szaggatott vonal mint tengely mentén 1 s alatt vízszintes helyzetbe fordul. A hurok teljes egészében függőlegesen felfelé irányuló, homogén mágneses mezőben van.

\(\displaystyle a)\) Melyik esetben nagyobb a hurkon átmenő mágneses fluxus?
\(\displaystyle b)\) Mekkora az indukált áram átlagos nagysága, és milyen az iránya, miközben a kis félkör lefordul?
\(\displaystyle c)\) Mekkora az indukált áram maximális értéke, ha a kis félkört állandó szögsebességgel forgatjuk, és éppen \(\displaystyle \Delta t=1\) s alatt kerül függőleges helyzetéből vízszintes helyzetbe?
Adatok: a mágneses indukcióvektor nagysága \(\displaystyle B=0{,}35~\rm T\), a hurok ellenállása \(\displaystyle R=0{,}025~ \Omega\), a kisebbik félkör sugara pedig \(\displaystyle r=0{,}2\) m.
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 5206. Határozzuk meg az uránból két \(\displaystyle \alpha\)-átalakulás és két \(\displaystyle \beta\)-bomlás eredményeként keletkező ionium tömegszámát! Melyik elem izotópja az ionium?
Példatári feladat
(4 pont)
P. 5207. A müon (\(\displaystyle \mu^-\)) bomlékony elemi részecske, átlagos élettartama 2,197 \(\displaystyle \mu\)s, tömege 207 elektrontömeg, töltése megegyezik az elektronéval.
Egy részecskegyorsító tárológyűrűjében a gyűrű síkjára merőleges, homogénnek tekinthető mágneses tér van. A gyűrű egy adott pontjánál érintő irányból monoenergetikus müonnyalábot vezetnek a tárológyűrűbe. A körpályán keringő müonok átlagosan 5 teljes kör megtétele után maguktól elbomlanak.
\(\displaystyle a)\) Mekkora a müonok (átlagos) sebessége és mozgási energiája, ha a tárológyűrű átmérője 120 m?
\(\displaystyle b)\) Mekkora a gyűrűben a mágneses indukció nagysága?
Közli: Fajszi Bulcsú, Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
