A KöMaL 2015. áprilisi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
C-jelű feladatokA beküldési határidő 2015. május 11-én LEJÁRT. |
C. 1287. Egy elég nagy négyzethálós lapra csigavonalban haladva felírjuk a pozitív egész számokat az ábra szerint. Melyik számok állnak a 2015 felett és alatt?
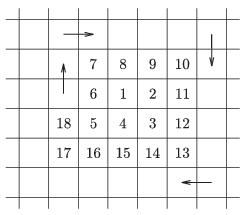
(5 pont)
C. 1288. Az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AB\) oldalának a \(\displaystyle B\) csúcshoz közelebb eső harmadolópontja \(\displaystyle H\), a \(\displaystyle BC\) oldal felezőpontja pedig \(\displaystyle F\). Milyen arányban osztja az \(\displaystyle AF\) és \(\displaystyle DH\) szakaszok metszéspontja ezeket a szakaszokat?
(5 pont)
C. 1289. Van 5 darab ötforintos, 10 darab tízforintos és 20 darab húszforintos pénzérménk. Hányféleképpen válthatunk fel 500 Ft-ot a pénzérmék felhasználásával?
(5 pont)
C. 1290. Oldjuk meg az \(\displaystyle (x;y)\) egész számpárok körében a \(\displaystyle 2xy+2x-5y=40\) egyenletet.
(5 pont)
C. 1291. Az \(\displaystyle x\)-tengely mely pontjából látszik legnagyobb szögben az \(\displaystyle A(2;4)\) és \(\displaystyle B(6;1)\) pontok által meghatározott szakasz?
(5 pont)
C. 1292. Oldjuk meg a \(\displaystyle \big(3\sqrt{3}\,\big)^n- \big(2\sqrt{2}\,\big)^n =2^n+3^n+\sqrt{6}^{\,n}\) egyenletet a pozitív egészek körében.
(5 pont)
C. 1293. Az Alfa sportszergyártó négyesével csomagolja a teniszlabdákat: gúlába rendezve egy szabályos tetraéder alakú dobozba (1. ábra). Az AFLA cég szintén négyesével csomagolja a teniszlabdákat: egymásra téve egy hosszú henger alakú (alul-felül zárt) dobozba (2. ábra). Mekkora az eltérés a kétféle doboz felülete között, ha egy teniszlabda átmérője 6,50 cm?
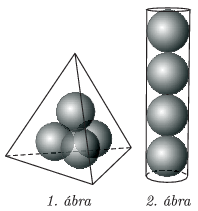
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2015. május 11-én LEJÁRT. |
B. 4705. Legyen \(\displaystyle p\) páratlan prímszám. Mutassuk meg, hogy az
\(\displaystyle x^2 + px = y^2 \)
egyenletnek pontosan egy megoldása van a pozitív egész számpárok körében.
Javasolta: Németh Balázs (Budapesti Fazekas M. Gyak. Gimn., 9. évf.)
(4 pont)
B. 4706. Az \(\displaystyle ABCD\) téglalap oldalai \(\displaystyle AB= \frac{\sqrt{5}+1}2\) és \(\displaystyle BC=1\). Legyen \(\displaystyle E\) az \(\displaystyle AB\) szakasz azon belső pontja, amelyre \(\displaystyle AE=1\). Mutassuk meg, hogy
\(\displaystyle ACE\sphericalangle= 2\cdot EDB\sphericalangle. \)
Javasolta: Miklós Szilárd (Herceghalom)
(3 pont)
B. 4707. Legyen \(\displaystyle t>1\) páratlan egész szám. Mutassuk meg, hogy csak véges sok olyan, \(\displaystyle t\)-nél nem kisebb \(\displaystyle n\), \(\displaystyle k\) egészekből álló pár létezik, amelyre \(\displaystyle S=\binom{n}{t} + \binom{k}{t}\) prím.
Javasolta: Maga Balázs (Budapest)
(5 pont)
B. 4708. Az \(\displaystyle ABC\) hegyesszögű háromszög körülírt körének középpontja \(\displaystyle O\), magasságpontja \(\displaystyle M\). Tükrözzük az \(\displaystyle A\) pontot a \(\displaystyle BC\) oldal felezőmerőlegesére, a \(\displaystyle B\) pontot a \(\displaystyle CA\) oldal felezőmerőlegesére, végül a \(\displaystyle C\) pontot az \(\displaystyle AB\) oldal felezőmerőlegesére, a tükörképek rendre \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\). Legyen az \(\displaystyle A_1B_1C_1\) háromszög beírt körének középpontja \(\displaystyle K\). Bizonyítsuk be, hogy az \(\displaystyle O\) pont felezi az \(\displaystyle MK\) szakaszt.
Javasolta: Bíró Bálint (Eger)
(5 pont)
B. 4709. Oldjuk meg az
\(\displaystyle x^{2}+y^{2}=13,\)
\(\displaystyle x^{3}+y^{3}=35\)
egyenletrendszert.
Javasolta: Szoldatics József (Budapest)
(3 pont)
B. 4710. A síkbeli \(\displaystyle \mathcal P\) ponthalmazról tudjuk, hogy minden egységsugarú körlemez a belsejében tartalmazza legalább egy pontját. Igaz-e, hogy biztosan van olyan egységsugarú zárt körlemez, amely legalább három \(\displaystyle \mathcal P\)-beli pontot tartalmaz?
(4 pont)
B. 4711. Legyen \(\displaystyle f(x)=\frac{4^x}{4^x+2}\). Számítsuk ki az
\(\displaystyle f(0/2015)+ f(1/2015)+f(2/2015)+\ldots +f(2014/2015)+f(2015/2015) \)
összeg értékét.
(5 pont)
B. 4712. Hány százalékát pazaroljuk el egy ceruzának? Tegyük fel, hogy a ceruza végtelen hosszú henger alakú, és benne a grafit is egy hengeres rúd, a hengerek tengelye pedig egybeesik. Kihegyezzük a ceruzát úgy, hogy a grafit hegye tökéletes kúp alakú, melynek nyílásszöge 12 fok. A használat során a ceruza és a papírlap által bezárt szög mindig 42 fok. Egészen addig használjuk a ceruzát, amíg már akárhogyan is forgatjuk a tengelye körül, nem tudunk írni vele, mert a fa karcolni kezdi a papírt. Ekkor újra kihegyezzük a ceruzát, egészen addig, hogy a ceruza hegye újra 12 fokos kúp legyen, de nem tovább, vagyis a grafit hegyének csúcsa nem változik a hegyezés során, az csak a használat során kopik. A grafit hány százalékát pazaroljuk el azzal, hogy a hegyezések során mindig valamennyit leforgácsolunk? Többet vagy kevesebbet pazarol az, aki 45 fokban tartja a ceruzát, és mennyivel?
Javasolta: Gáspár Merse Előd (Budapest)
(5 pont)
B. 4713. Az \(\displaystyle ABC\) háromszög \(\displaystyle B\) és \(\displaystyle C\) csúcsain áthaladó kör az \(\displaystyle AB\) oldalt \(\displaystyle D\)-ben, az \(\displaystyle AC\) oldalt \(\displaystyle E\)-ben metszi. A \(\displaystyle CD\) és \(\displaystyle BE\) egyenesek metszéspontja \(\displaystyle O\). Legyen \(\displaystyle M\) az \(\displaystyle ADE\), \(\displaystyle N\) pedig az \(\displaystyle ODE\) háromszög beírt körének középpontja. Bizonyítsuk be, hogy az \(\displaystyle MN\) egyenes felezi a kisebbik \(\displaystyle DE\) ívet.
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2015. május 11-én LEJÁRT. |
A. 641. Van-e a síkbeli négyzetrácsnak olyan \(\displaystyle S\) véges, nemüres részhalmaza, amelyben minden pontnak legalább két szomszédja szintén \(\displaystyle S\)-beli, és \(\displaystyle S\) nem tartalmaz négy olyan pontot, amelyek egy (nem feltétlenül tengelypárhuzamos) négyzet csúcsai?
Javasolta: Sustik Mátyás (San Francisco)
(5 pont)
A. 642. Legyen \(\displaystyle n\ge3\), és legyenek \(\displaystyle x_1,\ldots,x_n\) nemnegatív számok, továbbá legyen \(\displaystyle A=\sum_{i=1}^n x_i\), \(\displaystyle B=\sum_{i=1}^n x_i^2\) és \(\displaystyle C=\sum_{i=1}^n x_i^3\). Igazoljuk, hogy
\(\displaystyle (n+1)A^2B + (n-2)B^2 \ge A^4 + (2n-2)AC. \)
(5 pont)
A. 643. Tetszőleges pozitív egész \(\displaystyle n\) esetén jelöljük \(\displaystyle P(n)\)-nel az \(\displaystyle n^2+1\) legnagyobb prímosztóját. Mutassuk meg, hogy végtelen sok olyan \(\displaystyle (a,b,c,d)\), pozitív egészekből álló számnégyes létezik, amire \(\displaystyle a<b<c<d\) és \(\displaystyle P(a)=P(b)=P(c)=P(d)\).
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

