KöMaL Problems in Physics, November 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 11, 2017. |
M. 372. Make a sandglass from a cylinder-shaped plastic (PET) water bottle. Make a small hole (of diameter approximately 8-10 mm) on the bottle cap through which the dry sand can flow out. Measure how the amount of the out-flowing sand in a unit of time depends on the height of the sand in the bottle.
(6 pont)
 |
Problems with sign 'G'Deadline expired on December 11, 2017. |
G. 613. A vehicle undergoes circular motion at a constant speed of 72 km/h. How much time elapses until it gets back to the same point if its acceleration is 1.6 m/s\(\displaystyle {}^2\)?
(3 pont)
solution (in Hungarian), statistics
G. 614. Disks of equal mass of \(\displaystyle m\) were attached to the ends of a negligible-mass spring of spring constant \(\displaystyle D\). The disks and the spring in unstretched position are placed to an air-cushioned table, and they are given a velocity of \(\displaystyle v_0\) in the direction of the axis of the spring. At a certain instant the disk at the back is suddenly stopped and held at rest.
\(\displaystyle a)\) How much time elapses until the other disk turns back?
\(\displaystyle b)\) What is the greatest extension of the spring and at most how much potential energy is stored in the spring?
Data: \(\displaystyle D=16\) N/m, \(\displaystyle m=0.25\) kg, \(\displaystyle v_0=2\) m/s.
(3 pont)
solution (in Hungarian), statistics
G. 615. A container, filled with water halfway, is sliding down (with some acceleration) along a long enough slope of angle of elevation of \(\displaystyle 30^\circ\). What is the angle between the surface of the water and the plane of the slope, if friction is negligible?
(3 pont)
solution (in Hungarian), statistics
G. 616. The radius of a thin-walled, negligible-mass gymnastic ball is 30 cm, the pressure of the enclosed air is \(\displaystyle 1.1\cdot10^5\) Pa, and the ambient air pressure is \(\displaystyle 1.0\cdot10^5\) Pa. How much does the volume of the ball decrease when a 50 kg person sits upon it with her total weight, if in this case the ball touches the ground along a circle of radius 10 cm? The temperature of the air is constant.
(4 pont)
 |
Problems with sign 'P'Deadline expired on December 11, 2017. |
P. 4970. A vehicle travels from city \(\displaystyle A\) to city \(\displaystyle B\). During the first part of the journey its average speed is \(\displaystyle v_1\) whilst in the rest of the journey it is \(\displaystyle v_2\). By what factor is the length of the second part of the journey longer than that of the first part if the average speed calculated for the whole journey is
\(\displaystyle a)\) the arithmetic mean;
\(\displaystyle b)\) the geometric mean;
\(\displaystyle c)\) the harmonic mean;
\(\displaystyle d)\) the weighted arithmetic mean of ratio \(\displaystyle 1:k\) of the average speeds calculated for the two parts of the journey?
(4 pont)
solution (in Hungarian), statistics
P. 4971. A container, filled with water halfway, is sliding down with some acceleration along a long enough slope of angle of elevation of \(\displaystyle 30^\circ\). What is the angle between the plane of the slope and the surface of the water if the coefficient of kinetic friction between the container and the slope is 0.2?
(4 pont)
solution (in Hungarian), statistics
P. 4972. One end of a piece of unstretchable, light thread of length \(\displaystyle \ell\) is suspended, whilst the other end is attached to a small ring which can slide without friction along a horizontal rod – at a height of \(\displaystyle d<\ell\) above the point of suspension. The thread is held tight, and next to the rod a small object of mass \(\displaystyle m\) is placed by means of a pulley onto the thread, and then the system is released.
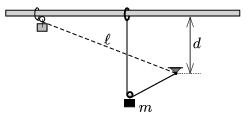
\(\displaystyle a)\) What will the speed of the object be at the lowermost point of its path?
\(\displaystyle b)\) Along what kind of curve does the object move?
\(\displaystyle c)\) What is the extension in the thread at the lowermost point of the path?
(5 pont)
solution (in Hungarian), statistics
P. 4973. During a lecture given by Baintner, Géza (1892–1980) there was an experiment shown, that when three rubber strings are tied in a Y shape, and the two strings at the two symmetrical ends of the Y are vibrated totally out of phase, then the two waves cancel each other, and the third piece of the Y stayed at rest. Question: What happens to the energy of the two waves?
(4 pont)
solution (in Hungarian), statistics
P. 4974. A thermally insulated cylinder is attached to a trolley. In the cylinder an easily moveable, and thermally insulated piston of mass \(\displaystyle M=20\) kg separates two chambers of volume \(\displaystyle V_0=50\) L, both containing air at a temperature of \(\displaystyle T_0=300\) K, and at a pressure of \(\displaystyle p_0=10^5\) Pa. The trolley moves towards a wall with speed \(\displaystyle v = 10\) m/s, with which it collides totally inelastically. At most what may the temperature of the air be in that chamber which is closer to the wall?
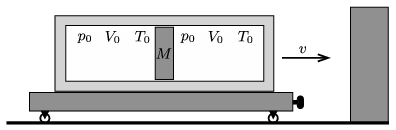
(5 pont)
solution (in Hungarian), statistics
P. 4975. During an experiment carried out in a laboratory on the Earth, a small object of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) is released in uniform horizontal magnetic field of induction \(\displaystyle B\). (It can be assumed that \(\displaystyle mg < QBc\) where \(\displaystyle c\) is the speed of light.) The motion of the object is observed until it reaches its lowermost position.
\(\displaystyle a)\) What is the greatest speed of the object?
\(\displaystyle b)\) To what depth does it sink?
\(\displaystyle c)\) What is its average speed along the horizontal direction?
\(\displaystyle d)\) What is the acceleration of the object at the lowermost point of its path?
(5 pont)
solution (in Hungarian), statistics
P. 4976. Three small balls are placed along a straight line, such that initially they do not move, and the distance between two neighbouring balls is \(\displaystyle d\). The masses and the charges of the balls are \(\displaystyle m\), \(\displaystyle 2m\), \(\displaystyle 5m\) and \(\displaystyle q\), \(\displaystyle q\), \(\displaystyle 2q\), respectively.
\(\displaystyle a)\) What is the distance between the balls, and what is their velocity when a very short time of \(\displaystyle t_0\) elapses after the balls start to move?
\(\displaystyle b)\) What is the speed of the balls after a long enough time?
(Apart from the electrostatic forces any other forces can be neglected.)
(5 pont)
solution (in Hungarian), statistics
P. 4977. The capacitors in the circuit shown in the figure are uncharged, before turning the switch on. At a certain moment the switch is closed. (Neglect the internal resistance of the voltage supply, the capacitance of the wires and the resistors, and the inductance of any of the elements in the circuit.)
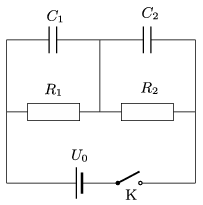
Sketch a graph of the voltage across the capacitors as a function of time.
Data: \(\displaystyle C_1=150~\mu\)F, \(\displaystyle C_2=50~\mu\)F, \(\displaystyle R_1=40~\rm k\Omega\), \(\displaystyle R_2=10~\rm k\Omega\), \(\displaystyle U_0=100\) V.
(5 pont)
solution (in Hungarian), statistics
P. 4978. In the engine of an ion propulsion rocket positive heavy ions are accelerated, such that these ions flow through the nozzle, and this accelerates the rocket. There is an electron accelerator on the rocket as well, why is it necessary?
(3 pont)
solution (in Hungarian), statistics
P. 4979. A drop of mercury of radius \(\displaystyle R\) and of surface tension \(\displaystyle \alpha\) is floating in weightlessness. If the drop is placed into weak, uniform electric field of magnitude \(\displaystyle E_0\), then the drop will extend in the direction of the electric field, its shape is nearly a rotational ellipsoid. Estimate the length of the extended mercury drop.
(6 pont)
Upload your solutions above.
