KöMaL Problems in Mathematics, November 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2013. |
K. 349. Kate is younger than her husband, but the age of each of them is a two-digit number that consists of the same two digits. The sum of their ages equals 11 times the difference of their ages. How old is Kate?
(6 pont)
solution (in Hungarian), statistics
K. 350. Steve lives far away from his new workplace, so he decided to go to work by car. On the first day, he travelled at an average speed of 70 km/h (practically uniformly), and arrived 1 minute late. On the second day, he started out at the same time but travelled at an average speed of 75 km/h (practically uniformly) and arrived 1 minute early. How far does he live from his workplace?
(6 pont)
solution (in Hungarian), statistics
K. 351. Find such numbers of the form TARTAR, divisible by 49 such that the number of the form RATRAT obtained by rearranging the digits is also divisible by 49.
(6 pont)
solution (in Hungarian), statistics
K. 352. Make a 5×5 table, and fill it out with the numbers 1 to 25, left to right, top to bottom. Interchange the rows an arbitrary number of times, and then interchange the columns an arbitrary number of times. Add 7 to each entry of the ``mixed'' table obtained in this way. Finally, add the numbers along one of the diagonals. Prove that the result is always 100.
|
(6 pont)
solution (in Hungarian), statistics
K. 353. Where are those points P(x;y) in the rectangular coordinate plane for which xy-2y=3x-6?
(6 pont)
solution (in Hungarian), statistics
K. 354. The sum of the squares of a certain positive integer and its two neighbours can be expressed as the sum of five consecutive integers. How many three-digit numbers have this property?
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 10, 2012. |
C. 1140. Ann, Beth, Connie and Dora shared a room in a class trip. The girls were given 1 bottle of orange juice, 2 bottles of apple juice, 2 bottles of peach juice and 3 bottles of mineral water to take with them on the forest walk. In how many different ways can they distribute the drinks among themselves if everyone is to get two bottles?
Suggested by A. Balga, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1141. The last digit of n3+3n2+3n is 4 (n is a positive integer). What is the last digit of 4n2+5n+6?
(5 pont)
solution (in Hungarian), statistics
C. 1142. The points P, A, B and Q, in this order, lie on the same line such that PA=BQ, and a triangle ABC with interior angles of 36o, 72o, 72o can be constructed out of the three line segments. Let R be the intersection of the circle of radius CP centred at C and the extension of the line AC beyond C. Find the angles subtended by the line segment PQ at the points C and R.
(5 pont)
solution (in Hungarian), statistics
C. 1143. The first few terms of a number sequence are the even numbers etc. From a certain term onwards, the sequence continues as an arithmetic progression with a common difference of d=3. Which term is that if the sum of the first 50 terms of the sequence is 2985?
(5 pont)
solution (in Hungarian), statistics
C. 1144. Find the largest possible value of S=x2y+2x+3+2y+xy2, given that x2+y2=2.
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 10, 2012. |
B. 4482. In Elastica, only natural numbers less than ten thousand are known. These numbers are written down in a flexible way. The rule for Elastican numbers is as follows: each number is represented in the lowest possible base such that the resulting number have at most four digits. Unfortunately, the numbers represented in this way are not always possible to decode uniquely: For example, the four-digit Elastican number 1101 may mean 13 as well as 37. Is there a three-digit Elastican number that represents more than one natural number?
Based on the idea of T. Lakatos, Balassagyarmat
(3 pont)
solution (in Hungarian), statistics
B. 4483. On a white sheet of squared paper, 40 small squares are coloured red. Prove that it is possible to select 10 red squares such that no two of them have a point in common.
(3 pont)
solution (in Hungarian), statistics
B. 4484. Prove that the equation has no solution of positive integers x, y, z where z>1.
(5 pont)
solution (in Hungarian), statistics
B. 4485. What is the largest possible fraction of a triangle that can be covered by a square with all its vertices on the perimeter of the triangle?
Suggested by I. Légrádi, Sopron
(4 pont)
solution (in Hungarian), statistics
B. 4486. Let a and b be positive integers. How many non-negative integers n are there such that ? ([x] denotes the greatest integer not greater than x.)
Suggested by R. F. Stöckli, Buenos Aires
(5 pont)
solution (in Hungarian), statistics
B. 4487. Is there a plane that does not pass through any vertex of a regular octahedron but intersects all the faces?
Suggested by V. Vígh, Szeged
(5 pont)
solution (in Hungarian), statistics
B. 4488. Show that 168 cannot be expressed as the sum of the squares of two rational numbers.
(4 pont)
solution (in Hungarian), statistics
B. 4489. Given the points P1, P2, P3 and the distances e1, e2, e3, construct a circle such that the length of the tangent drawn from Pi is ei.
(5 pont)
solution (in Hungarian), statistics
B. 4490. P and Q are interior points on side AC of a non-isosceles triangle ABC such that . The interior angle bisectors drawn from A and C intersect the line segment BP at points K and L, and the line segment BQ at points M and N, respectively. Prove that the lines AC, KN and LM are concurrent.
Suggested by Sz. Miklós, Herceghalom
(6 pont)
solution (in Hungarian), statistics
B. 4491. The names of 100 convicts are placed in 100 numbered drawers in some order. Then the convicts are brought one by one from their cells in a random order, and each of them is allowed to pull out 50 drawers one by one. If he finds his own name in a drawer then he is led to a separate room. Otherwise all 100 convicts are executed immediately. Finally, if each of them succeeds, they are all set free. Show that, knowing the rules, the prisoners can follow a strategy that results in a larger than 30% probability of going free.
(6 pont)
 |
Problems with sign 'A'Deadline expired on December 10, 2012. |
A. 572. Two circles k1 and k2 with centres O1 and O2, respectively, intersect perpendicularly at P and Q. Their external homothety center is H. The line t is tangent to k1 at T1 and tangent to k2 at T2. Let X be a point in the interior of the two circles such that HX=HP=HQ, and let X' be the reflection of X about t. Let the circle XX'T2 and the shorter arc PQ of k1 meet at U1, and let the circle XX'T1 and the shorter arc PQ of k2 meet at U2. Finally, let the lines O1U1 and O2U2 meet at V. Show that VU1=VU2.
(5 pont)
A. 573. Let D={0,1,2,...,9} be the set of decimal digits, and let R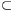 D×D be a set of ordered pairs of digits. An infinite sequence (a1,a2,a3,...) of digits is said to be compatible with R if (aj,aj+1)
D×D be a set of ordered pairs of digits. An infinite sequence (a1,a2,a3,...) of digits is said to be compatible with R if (aj,aj+1)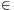 R for all positive integer j. Determine the smallest positive integer K with the property that if an arbitrary set R
R for all positive integer j. Determine the smallest positive integer K with the property that if an arbitrary set R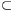 D×D is compatible with at least K distinct digit sequences then R is compatible with infinitely many digit sequences.
D×D is compatible with at least K distinct digit sequences then R is compatible with infinitely many digit sequences.
Based on the 5th problem of CIIM 2012, Guanajuato, Mexico
(5 pont)
A. 574. Let n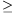 2 and let
2 and let be a polynomial with real coefficients. Prove that if for some positive integer k the polynomial (x-1)k+1 divides p(x) then
.
CIIM 2012, Guanajuato, Mexico
(5 pont)
Upload your solutions above.
