KöMaL Problems in Mathematics, January 2023
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2023. |
K. 749. Aladdin found five coins in a box. One of them is a counterfeit coin, and the monkey Abu is the only one who knows which. If Aladdin selects three coins and gives one of them to Abu, then Abu will tell him whether there is a counterfeit one among the other two. Whenever Abu gets a real coin, he will tell the truth, but he will lie if he gets a counterfeit coin. Is it possible to identify the counterfeit coin with at most three questions?
Based on the idea of S. Róka, Nyíregyháza
(5 pont)
solution (in Hungarian), statistics
K. 750. When Pete walks to the school, he always has the same speed. Sometimes he is in a hurry and then he runs, with twice the walking speed. Yesterday he walked the first third of the distance to the school and then covered the rest of the distance running. Today, he walked 6 minutes longer than the time spent running. How many minutes longer did it take him today to get to the school than yesterday?
(5 pont)
solution (in Hungarian), statistics
K. 751. We have five chocolate trufles, all of them look alike. However, three of them weigh 20 g each, one weighs 19 g, and one weighs 21 g. We want to identify the 19-g trufle with the help of an equal-arm balance only. Prove that it is possible to do it by using the balance three times, but less than three is not enough.
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on February 10, 2023. |
K/C. 752. There are \(\displaystyle k\) ways to select at least two of the numbers 10, 11, 12, 13, 14, 15, 16, 17 such that their sum is divisible by 3. In how many ways is it possible to select at least two of the numbers 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 such that their sum is divisible by 3? Express your answer in terms of \(\displaystyle k\). (Two selections are considered different if they do not consist of the same set of numbers.)
(5 pont)
solution (in Hungarian), statistics
K/C. 753. Points \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) and \(\displaystyle E\) lie on one arm of an angle of vertex \(\displaystyle A\), and points \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) and \(\displaystyle I\) lie on the other arm. Given that \(\displaystyle AB=BG=GD=DI=IE=EH=HC=CF=FA\) (see the figure), show that the triangles \(\displaystyle CEH\) and \(\displaystyle IGD\) are equilateral.
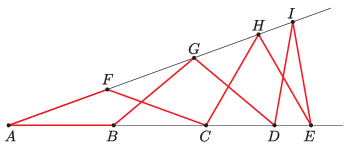
(5 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2023. |
C. 1748. Show that the shortest side of a cyclic quadrilateral inscribed in a unit circle cannot be longer than \(\displaystyle \sqrt{2}\,\).
(Canadian problem)
(5 pont)
solution (in Hungarian), statistics
C. 1749. Calculate the exact value of \(\displaystyle \sqrt[\scriptsize 3]{K}\), where \(\displaystyle K\) denotes the product of all positive factors of \(\displaystyle 2025\).
Proposed by K.\(\displaystyle \,\)A. Kozma, Győr
(5 pont)
solution (in Hungarian), statistics
C. 1750. \(\displaystyle M\) and \(\displaystyle N\) are the common points of circles \(\displaystyle k_1\), centred at \(\displaystyle O_1\) and \(\displaystyle k_2\), centred at \(\displaystyle O_2\). A secant drawn through point \(\displaystyle M\) intersects circle \(\displaystyle k_1\) at point \(\displaystyle A\) and circle \(\displaystyle k_2\) at point \(\displaystyle B\) such that \(\displaystyle A\) lies outside circle \(\displaystyle k_2\) and \(\displaystyle B\) lies outside circle \(\displaystyle k_1\). Lines \(\displaystyle AO_1\) and \(\displaystyle BO_2\) intersect at point \(\displaystyle P\). Points \(\displaystyle N\) and \(\displaystyle P\) lie in the same half plane determined by line \(\displaystyle O_1O_2\). Show that \(\displaystyle P\) lies on the circumscribed circle of triangle \(\displaystyle O_1NO_2\).
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1751. Let \(\displaystyle a\) and \(\displaystyle b\) denote positive real numbers such that \(\displaystyle a^2+b^2=\frac{2}{9}\). Prove that
\(\displaystyle \frac{1}{2-3a}+\frac{1}{2-3b} \ge 2. \)
Proposed by G. Szmerka, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1752. There are six people waiting in a line. It is taking very long, so they decide to play. They select a permutation of the six positions at random, and perform it three times successively. (A permutation is a rule of obtaining a new order by assigning a (possibly) new position to everyone. For example they may chose the following rule: the person at position 1 goes to position 3, the one at position 2 goes to position 1, the third goes to position 2, the fourth goes to position 6, the fifth stays in place, and the sixth goes to position 4.) What is the probability that at least one of them will be standing in their initial position at the end?
Proposed by K.\(\displaystyle \,\)A. Kozma, Győr
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2023. |
B. 5286. What is the smallest positive integer \(\displaystyle n\) for which the number \(\displaystyle \underbrace{11\ldots1}_{n}\) (in decimal notation) is divisible by the number \(\displaystyle \underbrace{33\ldots3}_{100}\)?
(Brasilian problem)
(3 pont)
solution (in Hungarian), statistics
B. 5287. Two circles touch each other externally. The line passing through the centres of the circles intersects the circles again at points \(\displaystyle A\) and \(\displaystyle B\). The points of tangency on one of the common external tangents of the circles are \(\displaystyle P\) and \(\displaystyle Q\), respectively. Prove that the lines \(\displaystyle AP\) and \(\displaystyle BQ\) intersect on the common internal tangent of the circles.
Proposed by I.\(\displaystyle \,\)Á. Molnár, Miskolc
(3 pont)
solution (in Hungarian), statistics
B. 5288. Two players are playing the following game on a \(\displaystyle 8 \times 8\) chessboard. They take turns in selecting one side of a field of the chessboard, separating two adjacent fields of the board, and colouring it yellow. The player who is first forced to create a closed yellow polygon will lose the game. Which player has a winning strategy?
Based on an American competition problem
(4 pont)
solution (in Hungarian), statistics
B. 5289. Let \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) denote non-negative real numbers such that \(\displaystyle a+b+c+d=1\). Prove that
\(\displaystyle \frac{1}{a^2+1}+\frac{1}{b^2+1}+\frac{1}{c^2+1}+\frac{1}{d^2+1} \ge \frac72. \)
Proposed by J. Szoldatics, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5290. Solve the following equation over the set of positive integers:
\(\displaystyle 3^n+4^n+\dots+{(n+2)}^n= {(n+3)}^n. \)
Proposed by T. Káspári, Paks
(6 pont)
solution (in Hungarian), statistics
B. 5291. The centre of the inscribed circle of a triangle \(\displaystyle ABC\) is \(\displaystyle I\), and the centre of its circumscribed circle is \(\displaystyle O\). Given that \(\displaystyle \angle OIA =90^\circ\), \(\displaystyle AI=89\) and \(\displaystyle BC=160\), what is the area of the triangle?
Proposed by S. Róka, Nyíregyháza
(5 pont)
solution (in Hungarian), statistics
B. 5292. Given a circle \(\displaystyle k\) and points \(\displaystyle P\) and \(\displaystyle Q\) in its interior, construct (write down the steps of the construction – basic construction steps like bisecting an angle, reflecting over a line, etc. do not need to be described in detail – and explain why the method is correct; it is not required to perform the construction on paper) a circle through points \(\displaystyle P\) and \(\displaystyle Q\) that intersects the circle \(\displaystyle k\) at two diametrically opposite points.
Depending on the position of points \(\displaystyle P\) and \(\displaystyle Q\), how many solutions will the problem have?
Proposed by G. Kató, Kápolnásnyék
(5 pont)
solution (in Hungarian), statistics
B. 5293. Let \(\displaystyle p\) denote a prime number. What is the largest number of polynomials with integer coefficients such that there are no pairs of polynomials such that the value of their difference is divisible by \(\displaystyle p^2\) at every integer?
Proposed by P.\(\displaystyle \,\)P. Pach, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2023. |
A. 842. \(\displaystyle n\) people live in a town, and they are members of some clubs (residents can be members of more than one club). No matter how we choose some (but at least one) clubs, there is a resident of the town who is the member of an odd number of the chosen clubs. Prove that the number of clubs is at most \(\displaystyle n\).
Proposed by Dömötör Pálvölgyi, Budapest
(7 pont)
A. 843. Let \(\displaystyle N\) be the set of those positive integers \(\displaystyle n\) for which \(\displaystyle n\mid k^k-1\) implies \(\displaystyle n\mid k-1\) for every positive integer \(\displaystyle k\). Prove that if \(\displaystyle n_1,n_2\in N\), then their greatest common divisor is also in \(\displaystyle N\).
(7 pont)
A. 844. The inscribed circle of triangle \(\displaystyle ABC\) is tangent to sides \(\displaystyle BC\), \(\displaystyle AC\) and \(\displaystyle AB\) at points \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\), respectively. Let \(\displaystyle E'\) be the reflection of point \(\displaystyle E\) across line \(\displaystyle DF\), and \(\displaystyle F'\) be the reflection of point \(\displaystyle F\) across line \(\displaystyle DE\). Let line \(\displaystyle EF\) intersect the circumcircle of triangle \(\displaystyle AE'F'\) at points \(\displaystyle X\) and \(\displaystyle Y\). Prove that \(\displaystyle DX=DY\).
Proposed by Márton Lovas, Budapest
(7 pont)
Upload your solutions above.
