| [157] lorantfy | 2003-12-05 18:27:14 |
 Kedves Károly, Gyuri és Fórumosok!
Az ügyvédeknek nem szabad bedőlni és persze az ügyvédes feladatoknak sem!
Az egész megoldás csak ennyi (próbálom részletezni amit [143]-ban leírtam):
Amikor az ügyvéd azt mondja: Ha szombat estig életben hagynak, akkor már vasárnap nem végezhetnek ki… akkor valójában a következő feltételre támaszkodik: Ha szombat estig nem végeznek ki, akkor vasárnap már nem végezhetnek ki. Ezzel mindenki egyet is ért és nem is gondol arra, hogy a kiinduló feltétel hamis, hiszen bármelyik napon kivégezhetik vasárnap előtt. Csakhogy most ebből a hamis feltételbők kapott „igazságból” (mármint, hogy vasárnap nem végezhetik ki) kiindulva következtet visszafelé.
Valójában az ügyvéd csak ennyit állít: Ha szombat estig nem végeznek ki, akkor sem hétfőn, sem kedden, sem …szombaton nem végeztek ki és vasárnap már nem fognak. De ha szombatig kivégeznének (I’m sorry!) akkor az egész következtetés alapját vesztett hülyeség.
A megfogalmazásban (aláhúzott rész) direkt nem szerepel a kivégzés szó, helyette: életben hagynak! Az is mindegy melyik nap végzik ki. Akár hétfőn is kivégezhették volna.
|
| Előzmény: [153] Hajba Károly, 2003-12-05 01:04:38 |
|
| [156] SchZol | 2003-12-05 12:19:47 |
 Itt egy másik megoldás a 36.feladatara:
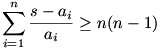
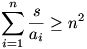
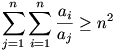
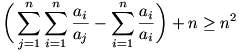
Itt a zárójelben az a1,a2...ai számok összes lehetséges hányadosa szerepel, amiket párokba csoportosítva számok és reciprok összegeit kapjuk. A lehetséges párosítások száma: 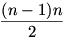 . Mivel minden tag pozitív ezért ezek minimuma . Mivel minden tag pozitív ezért ezek minimuma
(n-1)n.
Ebből következik hogy a kifejezés minimuma n(n-1)+n azaz n2.
Tehát az állítást igazoltuk. Remélem semmit nem írtam el.
|
| Előzmény: [151] Pach Péter Pál, 2003-12-04 23:35:55 |
|
|
| [154] Hajba Károly | 2003-12-05 09:16:01 |
 31. feladat:
Gyakorlatilag a lényeget BrickTop már elmondta, de egy kicsit pontatlanul, így a faladat általa kialakított megoldását pontosítom.
A sorban az utolsó nyilatkozik először és a következő mindig az nyilatkozó előtti személy. Mivel 99 sapkát lát, az egyik páros, a másik páratlan. Ő a páros számú színt mondja. Neki így is van 50
Mindenki figyeli, hogy hányszor mondják időben előttük ezt a szint és minden elhangzáskor váltják a paritását. Továbbá mindenki tudja, hogy előtte páros vagy páratlanul van-e ez a szín, az első párosszámot lát. Amennyiben a két paritás ellentétes az adott szín van a fején, míg azonosság esetén az ellentétes szín.
Így akár 100 %-osan is megmenekülhetnek a smasszerek legnagyobb megrökönyödésére. De ha valaki elhibázza, az utánuk következőknek annyi. :o)
HK
|
| Előzmény: [131] Gyuri, 2003-12-03 00:29:47 |
|
| [153] Hajba Károly | 2003-12-05 01:04:38 |
 Kedves Gyuri!
A feladat tökéletesen írja le az ügyvédeket, a tárgyalás alatt mindig minden jól áll, de a végén kiderül, hogy Ő nem teljesítménykötelmes, azaz a díja pervesztés esetén is jár neki (no meg a szája :o)
No, de térjünk vissza a feladathoz! Képzeletben játszuk el a következő játékot, melyet többszázszor is lejátszunk. A kivégzés napját véletlenül jelöljük ki és ezt ütköztetjük a különböző elképzelhető stratégiákkal, azaz ha a stratégia eltalálja a kivégzés napját +1 pontot kap, míg ha nem kap pontot. A stratégiák eredményességéből lehet következtetni a feladat megoldására is.
Az ügyvéd stratégiája nyilvánvalóan rossz, mivel egy pontot sem szerez.
A legtöbb pontot talán az a stratégia szerez, mely a kivégzés napját véletlenszerűen a H-P között határozza meg, azaz ebben az időszakban fogják kivégezni.
De mindentől függetlenül nem tudom a helyes megoldást, még az is lehet, hogy az ügyvédnek volt igaza?!
HK
|
| Előzmény: [133] Gyuri, 2003-12-03 01:21:26 |
|
| [152] Hajba Károly | 2003-12-05 00:31:47 |
 Megoldás a 29. feladatra:
Legyen # - fekete, míg O - fehér sapka, továbbá az ábra szerint 3-2-1 sorszámrend:
A)
# O O
3 (azonnal): [Mivel nem lehet több fehér sapka,] fekete.
# # O és O # O
2 (kicsit később): [Mivel 3 nem szólt azonnal, így 1 és én nem mind fehér, mivel 1 fehér,] fekete.
# O #, # # #, O O # és O # #
1 (kicsit később): [Mivel 3 nem szólt azonnal, így 1 és én nem mind fehér.] (kicsit később) [Mivel 2 nem szól, nem lehetek fehér,] fekete
B)
# O O = 1: fekete :O( - 2: fekete :O( - 3: fekete :O)
# # O = 1: fekete :O( - 2: fekete :O) - 3:O(
O # O = 1: fekete :O( - 2: fekete :O) - 3:O(
# O # = 1: fekete :O) - 2:O( - 3:O(
# # # = 1: fekete :O) - 2:O( - 3:O(
O O # = 1: fekete :O) - 2:O( - 3:O(
O # # = 1: fekete :O) - 2:O( - 3:O(
Tehát mindkét esetben 1 - 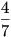 | 2 - | 2 - 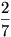 | 3 - | 3 - 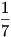 , holott 1 nem lát senkit. , holott 1 nem lát senkit.
HK
|
| Előzmény: [128] lorantfy, 2003-12-02 21:42:13 |
|
| [151] Pach Péter Pál | 2003-12-04 23:35:55 |
 Megoldás a 36. feladatra
Adjunk mindkét oldalhoz n-et!
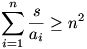
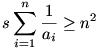
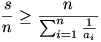
Ez viszont éppen a számtani és harmonikus középek közti egyenlőtlenség. (Pozitív számokra írtuk fel.) Ekvivalens lépéseket hajtottunk végre, így bizonyítottuk az eredeti egyenlőtlenséget.
Ez a feladat speciális esete egy általánosabb (egyébként ukrán) feladatnak. A feladat a következő:
38. feladat
a1,a2,…,an pozitív valós számok és k<n.
Ha A={i1,i2,…,ik} {1,2,…,n}=Nn és {j1,j2,…,jn-k}=Nn\A, akkor legyen {1,2,…,n}=Nn és {j1,j2,…,jn-k}=Nn\A, akkor legyen

Bizonyítsuk be, hogy
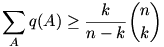
A 36. feladatban k=n-1 volt.
|
| Előzmény: [148] SchZol, 2003-12-04 20:09:45 |
|
| [150] lorantfy | 2003-12-04 23:01:54 |
 Csak a [23]-as volt, amit [36]-ban Géza félmegoldásnak értékelt - fél túrórudival - azután más nem foglalkozott vele. Fálesz Mihályt hiányolom! A nemkockafejűek témában láttam utoljára aztán nyoma veszett. Hol vagy Mihály...?
|
| Előzmény: [149] Pach Péter Pál, 2003-12-04 22:19:50 |
|
| [149] Pach Péter Pál | 2003-12-04 22:19:50 |
 A [23]-as hozzászólás után Fálesz Mihály készített egy felsorolást a még megoldatlan példákról [49]-ben, és ott szerepelt a 3. feladat is. Csak nem tudtam, hogy később érkezett-e rá teljes megoldás. Szerintem mindenki nevében köszönet illet benneteket a még megoldatlan példák felsorolásáért. :-)
|
| Előzmény: [146] Hajba Károly, 2003-12-04 12:44:52 |
|
| [148] SchZol | 2003-12-04 20:09:45 |
 December 3-án került megrendezésre az idei Cornides István Matematika - Fizika Emlékverseny. Íme a 12.évfolyamosok matek feladatai:
35.feladat (A verseny 1.feladata)
Határozza meg, mely p valós számokra van az
x3+px2+2px=3p+1
egyenletnek három különböző  , , , , valós gyöke, amelyre valós gyöke, amelyre  . . = = 2. 2.
36.feladat (A verseny 2.feladata)
Jelölje s az a1,a2,...,an pozitív valós számok összegét. Igazoljuk, hogy
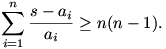
37.feladat (A verseny 3.feladata)
Az ABCD paralelogramma S belső pontjára teljesül, hogy az ASB =CSD =CSD =90o. =90o.
Bizonyítsuk be, hogy SBC =SDC =SDC . .
|
|







 {1,2,…,n}=Nn és {j1,j2,…,jn-k}=Nn\A, akkor legyen
{1,2,…,n}=Nn és {j1,j2,…,jn-k}=Nn\A, akkor legyen ,
, ,
, valós gyöke, amelyre
valós gyöke, amelyre  =CSD
=CSD