Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] [212] [213] [214] [215] [216] [217] [218] [219] [220] [221] [222] [223] [224] [225] [226] [227] [228] [229] [230] [231] [232] [233] [234] [235] [236] [237] [238] [239] [240] [241] [242] [243] [244] [245] [246] [247] [248] [249] [250] [251] [252] [253] [254] [255] [256] [257] [258] [259] [260] [261] [262] [263] [264] [265] [266] [267] [268] [269] [270] [271] [272] [273] [274] [275] [276] [277] [278] [279] [280] [281] [282] [283] [284] [285] [286] [287] [288] [289] [290] [291] [292] [293] [294] [295] [296] [297] [298] [299] [300] [301] [302] [303] [304] [305] [306] [307] [308] [309] [310] [311] [312] [313] [314] [315] [316] [317] [318] [319] [320] [321] [322] [323] [324] [325] [326] [327] [328] [329] [330] [331] [332] [333] [334] [335] [336] [337] [338] [339] [340] [341] [342] [343] [344] [345] [346] [347] [348] [349] [350] [351] [352] [353] [354] [355] [356] [357] [358] [359] [360] [361] [362] [363] [364] [365] [366] [367] [368] [369] [370] [371] [372] [373] [374] [375] [376] [377] [378] [379] [380] [381] [382] [383] [384] [385] [386] [387] [388] [389] [390] [391] [392] [393] [394] [395] [396] [397] [398] [399] [400] [401] [402]

Szeretnél hozzászólni? Jelentkezz be.

[765] Atosz

2005-01-30 08:22:27

Sziasztok!

Azt hiszem meg van a megoldás. Káli gúla hozzászólása ébresztett rá arra, hogy egy szomszédos 6-os tartományba lépés valsége nagyobb mint 1, hiszen ezek nem függetlenek egymástól. Az utolsó dobás alapján elkezdtem a rekurziót visszafejteni és kaptam, hogy

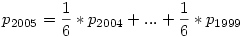
$p_{2005}=\frac{1}{6}*p_{2004}+...+\frac{1}{6}*p_{1999}$

Ez azt jelenti, hogy a sorozat mindig az előző hat átlagával halad tovább és mivel az elejét ismerjük így onnan elindulva kiszámítható, hogy mennyi lesz p₂₀₀₅

Viszont ennél találtam egy gyorsabb megoldást is! Tekintsük azokat az eseményeket, amikor kimondom azt, hogy most már 1 dobással is beérhetek a célba. Ez 6 helyet jelent a 2005-ik előtt. Legyen A_i az az esemény, hogy a (2005-i)-ik helyen szólalok meg (i=1,...,6). Ezen események valségei p_Ai nem egyeznek meg a rálépés valségével, viszont függetlenek és összegük 1. Legyen ilyen távolságban a mezőre lépés valsége p (feltesszük, hogy már közel egyforma - éppen ezt keressük). A 2004-ik helyen akkor szólalok meg, ha előtte ráléptem az 1998-ikra és ott 6-ost dobtam, azaz 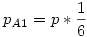$p_{A1}=p*\frac{1}{6}$ . 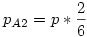A 2003-ik helyen akkor szólalok meg, ha az 1998-ik helyről érkezem 5-össel, vagy az 1997-ről 6-ossal, azaz $p_{A2}=p*\frac{2}{6}$ , stb...

Ha ezt mind felírjuk, kapjuk hogy

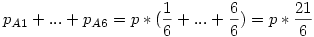
$p_{A1}+...+p_{A6}=p*(\frac{1}{6}+...+\frac{6}{6})=p*\frac{21}{6}$

Mivel ez 1, így

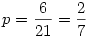
$p=\frac{6}{21}=\frac{2}{7}$

Természetesen ez csak akkor lesz pontosan igaz, ha a kérdéses hely tart a végtelenbe, de a 2005. már "jó közelítéssel" ennek tekinthető.

[764] SAMBUCA

2005-01-29 19:56:25

Hali!

A Kemény Legény által emlegetett cikk megtalálható itt.

SAMBUCA

[763] Kemény Legény	2005-01-29 16:00:57
Na a cikk a KöMaL elektronikus archivumában található meg,pl. rákeresve Kós Géza cikkeire,a Játék mindenkinek -et kiválasztva.A 11-es szám pedig a novemeber hónapot volt hivatott jelölni,kár hogy nem találtátok meg.

[762] Atosz

2005-01-29 13:25:05

Bolond vagyok!

Az előző hozzászólásomat tekintsétek semmisnek, hiszen pont ez a lényeg, a p_i-k összege nem 1.

[761] jenei.attila	2005-01-29 13:03:32
Nem lehet, hogy elírtál valamit? 1994-ben nem volt 11. szám. (Sőt, tudtommal máskor sem).
Előzmény: [757] Kemény Legény, 2005-01-29 10:23:59

[760] Atosz

2005-01-29 13:01:25

Egy újabb gondolat jutott eszembe, s közben láttam Káli gúla a segítségedet. Mindjárt végiggondolom, de közben beírom azt, amit akartam:

Egy szomszédos 6-os tartományba lépés összvalsége 1 kell hogy legyen, azaz p(n-6)+p(n-5)+...+P(n-1)=1. De a mellette lévő 6-os tartományra is ennek igaznak kell lennie, azaz p(n-6)=p(n). Ebből az következik, hogy minden 6. mezőre lépésnél egyforma valségek vannak, azaz P(2005)=p(1)= $\frac{1}{6}$

Ez vagy jó, vagy nem, de akkor hol van benne a hiba?

Előzmény: [759] Káli gúla, 2005-01-29 11:58:15

[759] Káli gúla	2005-01-29 11:58:15
Nem független a szomszédos mezőre lépés. P(n-6)+...+P(n-1)>1. A rekurziód jó, csak mást kell mondani. Mekkora volt az utolsó dobás?
Előzmény: [758] Atosz, 2005-01-29 11:32:25

[758] Atosz

2005-01-29 11:32:25

Pontosan hol van az a cikk, mert nem találom?

Engem leginkább az zavar a saját megoldásomban, hogy ha a 2004, 2003, 2002, 2001 2000, 1999 helyek valamelyikén egyforma valséggel leszünk, akkor miért nem $\frac{1}{6}$ jön ki a 2005-re? (mert akkor ugyanígy egyforma valséggel lennénk a 2005-2000 helyek valamelyikén is)

Előzmény: [757] Kemény Legény, 2005-01-29 10:23:59

[757] Kemény Legény	2005-01-29 10:23:59
Elnézést a közbeszólásért,de szerintem nem ennyi lesz a végeredmény és a megoldás sem ilyen egyszerű.De a legjobb lesz,ha elolvassátok Kós Géza cikkét az 1994/11. KöMaL-ban,ahol egy elég zuzó megoldást nyomat a problémára.

[756] Atosz

2005-01-29 09:53:17

Én a következőképp okoskodtam (remélem jól).

A dobálások után mindenképpen elérjük azt a helyzetet, amikor azt mondhatjuk, hogy innentől akár egy dobással is nyerhetünk. Ekkor 1,2,3...,6 egység távolságra leszünk a 2005. rácsponttól. Az, hogy milyen valséggel állunk éppen az egyik vagy másik helyen, az "jó közelítéssel" egyformán valószínű, azaz $\frac{1}{6}$ . 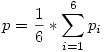(az origótól ekkora távolságban már az, hiszen ez a megfelelő távolságra lévő számok 1-6 számok összegeire való felbontások számától függ, ami közel egyforma) Innen a keresett valség $p=\frac{1}{6}*\sum_{i=1}^{6}{p_i}$

Itt már csak azt kell megvizsgálni, hogy egy adott távolságból hányféleképpen juthatunk célba. pl. 3 egység távolságból bejuthatunk a következő dobásokkal: (3) vagy (1,2) vagy (2,1) vagy (1,1,1). Egy egylépéses győzelem valsége 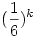$\frac{1}{6}$ , míg egy k lépésesé $(\frac{1}{6})^k$ , hiszen k-szor egymás után megfelelőt kell dobnunk. Ha megfigyeljük a megfelelő távolságokról a bejutásokat, akkor látjuk, hogy éppen 6 egylépéses, 15 kétlépéses, 20 háromlépéses, 15 négylépéses, 6 ötlépéses és 1 hatlépéses győzelem van. Ezek a számok éppen a Pascal háromszög megfelelő sorának tagjai (az első 1-es kivételével). Így

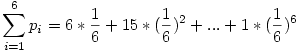
$\sum_{i=1}^{6}p_i=6*\frac{1}{6}+15*(\frac{1}{6})^2+...+1*(\frac{1}{6})^6$

Ami a binomiális tétel szerint ez éppen:

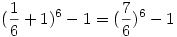
$(\frac{1}{6}+1)^6-1=(\frac{7}{6})^6-1$

Így a keresett valség:

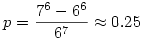
$p=\frac{7^6-6^6}{6^7}\approx0.25$

Előzmény: [755] Káli gúla, 2005-01-27 23:18:19

Már regisztráltál?
Új vendég vagy?