| [90] Kós Géza | 2005-07-31 10:25:20 |
 Elég rég láttam már igazi totószelvényt...
A totóban 13 labdarúgó mérkőzés eredményét kell megtippelni. (1=hazai győzelem; 2=vendéggyőzelem; X=döntetlen). A 13, 12, 11 és 10 találatos szelvényeket jutalmazzák. (Volt olyan idő, amikor a 0 találatosokra is fizettek valamit.) Van egy 14. meccs is, de az csak akkor számít, ha mind a 13-at eltaláltad. Ennek megfelelően van 13 és 13+1 találatos szelvény. Ha viszont csak 12 találatod van, akkor a +1 nem számít.
Az esetleg elmaradt meccsek pótlására volt régen még két tartalék meccs is. Aztán kitalálták, hogy az elmaradt meccsekre mesterségesen találnak ki eredményt.
* * *
A feladat tehát a következő. Vesszük az összes 13 hosszúságú 1-2-X sorozatok S halmazát. Ezek közül ki akarunk választani egy R részhalmazt úgy, hogy minden s S-hez létezzen olyan r S-hez létezzen olyan r R, hogy s és r legfeljebb egy helyen különbözik. Az a kérdés, hogy |R| mennyire lehet kicsi. R, hogy s és r legfeljebb egy helyen különbözik. Az a kérdés, hogy |R| mennyire lehet kicsi.
|
| Előzmény: [89] xviktor, 2005-07-30 23:59:33 |
|
| [89] xviktor | 2005-07-30 23:59:33 |
 A 30. feladattal kapcsolatban lenne kerdesem. A feladat szovege szerint csak az elso 13 szamit. Ez azt jelenti, hogy csupan 13 mezot toltunk ki, vagy hogy mind a 16ot, ahol az elso 13bol talalunk el 12ot?
Elore is koszonom a valaszt: Viktor
|
|
| [88] lorantfy | 2005-07-30 14:18:46 |
 Szia Jónás!
Kösz a részletes leírást, segítségével megértettem Géza kurtára szabott magyarázatát is.
(Mi van a képeden a háttérben? Egy oroszlán szobor?)
|
| Előzmény: [84] jonas, 2005-07-29 16:08:36 |
|
| [87] xviktor | 2005-07-29 17:54:23 |
 Azt szeretnem megkerdezni, hogy mikorra varhato a 29. feladat.
|
|
| [86] Kós Géza | 2005-07-29 17:01:04 |
 Van egy szép bizonyítás a Young képletre, ami a jól ismert kétdimenziós módszer általánosítása. Matektáborokban néha el szoktam mondani. :-)
Egyszer majd leírom, ha lesz egy kis időm...
|
| Előzmény: [83] lorantfy, 2005-07-28 09:49:12 |
|
| [85] Kós Géza | 2005-07-29 16:39:50 |
 Úgy lehet gyorsan számolni, hogy a w(x,y,z) értékét minden számhármasra kiszámoljuk, és tároljuk egy 9×9×9 méretű tömbben. Akkor a program pillanatok alatt lefut.
|
| Előzmény: [83] lorantfy, 2005-07-28 09:49:12 |
|
| [84] jonas | 2005-07-29 16:08:36 |
 Én felírtam egy hasonló rekurzív képletet, és megkaptam belőle a helyes eredményt.
Az én rekurzióm a következő:
a=b=c=8 rögzített paraméterek (a betűk számai);
g(m,n,k)=0 ha a<m vagy b<n vagy c<k;
g(m,n,k)=1 ha 8=m=n=k;
g(m,n,k)=g(m,n,1+k)+g(m,1+n,k)+g(1+m,n,k) ha m n n k; k;
g(m,n,k)=0 minden más esetben.
g(0,0,0) a keresett szám.
Ezt a következő módon kaptam. Tegyük fel, hogy már felírtunk egy szót, ami érvényes (minden prefixében legfeljebb annyi A van, mint B, és legfeljebb annyi B, mint C), és ebben m darab A, n darab B, k darab C van. Ekkor g(m,n,k) féle lehetséges befejezés van.
Ha m<n vagy n<k akkor a szóban már túl sok A vagy B betű van, így a szó szabálytalan. Ilyenkor g(m,n,k)-t nullának tekintjük. Hasonló a helyzet, ha a<m vagy b<n vagy c<k, mert ekkor túl sok van valamelyik betűből.
Ha viszont m n n k, akkor a következő betű lehet A, B, vagy C, és az egyes esetekben g(1+m,n,k), g(m,1+n,k), illetve g(m,n,1+k) lehetséges befejezés van. Lehet, hogy valamelyik folytatás nem lehetséges, de ilyenkor a megfelelő helyettesítési érték nulla. k, akkor a következő betű lehet A, B, vagy C, és az egyes esetekben g(1+m,n,k), g(m,1+n,k), illetve g(m,n,1+k) lehetséges befejezés van. Lehet, hogy valamelyik folytatás nem lehetséges, de ilyenkor a megfelelő helyettesítési érték nulla.
Utána egyszerűen lefuttattam a rekurziót, és kijött g(0,0,0)=23371634.
Aztán kipróbáltam ugyanezt kisebb a=b=c értékekre is, és a Sloane-ben megtaláltam a A005789 sorozatot.
|
| Előzmény: [83] lorantfy, 2005-07-28 09:49:12 |
|
| [83] lorantfy | 2005-07-28 09:49:12 |
 A 27. feladathoz: A feladat feltételeinek eleget tevő 24 betűs szavak számát a w(a,b,c) rekurzív formula és a Young-formula ismerete nélkül is le lehet számolni egy egyszerű kis progival.
Generáljuk egy 24 elemű tömbben az összes 1,2,3 számjegyekből álló számot. Leszámoljuk a különböző számjegyek számát és kiválasztjuk azokat, ahol mindegyikből 8-8-8 db van. Megnézzük teljesül-e a "legalább annyi A..." feltétel, ha igen növeljük a számlálót.
Egyetlen szépséghibája, hogy kb. 4 óráig fut :-)
A feladat magyarázatában ezt a részt nem értem: "Ha a<b, b<c vagy c<0, akkor w(a,b,c)=0, w(0,0,0)=1,"
Megpróbálom belátni a w(a,b,c)-re megadott rekurzív képletet, de ha valakinek kapásból megy beírhatja ide!
Kós Gézának köszönöm az előző választ!
|
|
|
| [81] lorantfy | 2005-07-26 23:21:25 |
 Kedves Géza!
Nagyon szép a megoldás. Köszönöm, hogy föltetted, már nagyon fúrta az oldalamat!
A 28. feladattal kapcsolatban kérdezem:
"Megoldásnak egyetlen, két tizedesjegyig felírt valós számot várunk."
Ez azt jelenti, hogy két tizedesjegyre kerekített érték legyen, vagy azt, hogy vágjuk le a 2. tizedesjegy utáni számjegyeket?
|
| Előzmény: [80] Kós Géza, 2005-07-19 11:24:22 |
|
| [80] Kós Géza | 2005-07-19 11:24:22 |
 Leírom a 180-szöges megoldást.
Az ötletet Egy régi Csirmaz-cikkben olvastam.
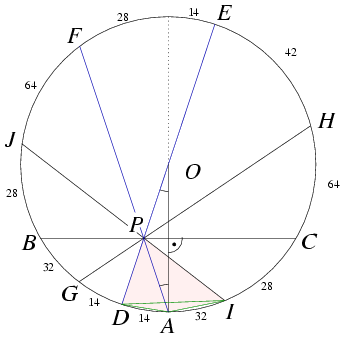
Legyen A egy pont az O középpontú körön. Az OA sugarat merőlegesen felező húr legyen BC. Ehhez a húrhoz, mint tudjuk, 120 fokos középponti szög tartozik, és a B,C,A pontok kiegészíthetők a körbe írt szabályos hatszöggé.
Rajzoljunk meg még egy DE átmérőt, ami a BC húrt P-ben metszi, és tükrözzük ezt az átmérőt a BC egyenesre. A tükörkép átmegy A-n; a körrel vett másik metszéspontja legyen F. Tükrözzünk most a DE átmérőre. Az AF húr tükörképe legyen GH, BC tükörképe pedig legyen IJ. Így 5 húrt találtunk, ami átmegy a P ponton.
Ha az AOD szöget 14 foknak választjuk, akkor az egyes ívekhez az ábrán látható szögeket kapjuk. A tesztversenybeli feladat az AP és DI szakaszok szögének meghatároszása. A cikkben látott módon, a kerületi és középponti szögek tételéből 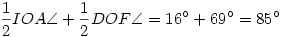 . .
|
 |
| Előzmény: [70] lorantfy, 2005-07-12 23:34:59 |
|
| [79] Atosz | 2005-07-18 14:11:01 |
 Sziasztok!
Még mindig a 85 fokos feladatra találtam egy geometriaibb jellegű, de trigonometriát is használó megoldást, ám itt nem kellett az egyenletben a 85 fokot bepróbálni, hanem kijött magától.
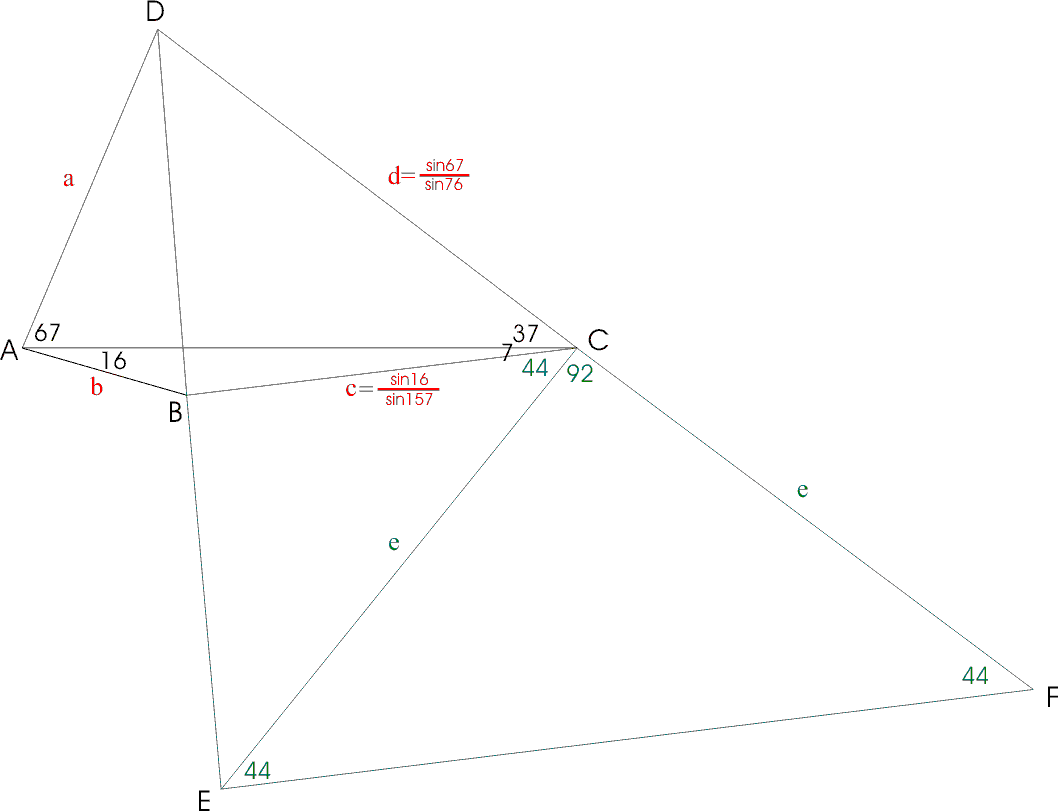
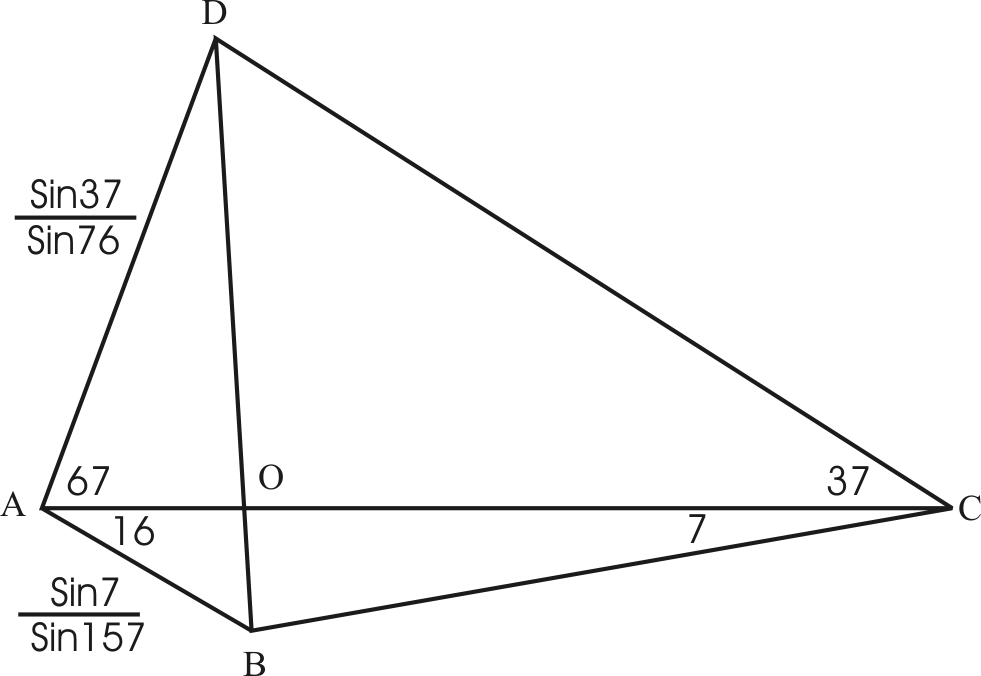
A lenti ábrán AC-t 1-nek véve felírtam egy-egy szinusz-tételt a c és d oldalakra, majd kiegészítettem az eredeti ábrát következőképpen:
C-ből indulva húztam egy egyenest 37+7=44 fokos szögben és ez elmetszette a DB hosszabbítását E-ben, majd E-ből egy párhuzamost BC-vel, ami elmetszette a DC hosszabbítását F-ben. Mivel a CDE háromszögben BC szögfelező, így CF=CE-vel. Párhuzamos szelők tételét használva kapjuk, hogy EF:c=(e+d):d, ami alapján
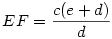
A CFE háromszögre felírva a szinusz-tételt, a következő eredményt kapjuk
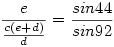
Ezt rendezve kapjuk, hogy
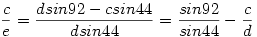
Beírva c és d helyére a megfelelő értékeket kapjuk, hogy
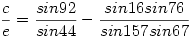
Alkalmazva
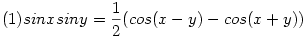
és a
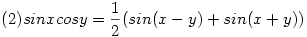
összefüggéseket kapjuk (itt egy pár sor kihagyva és a közös nevezőnek 2sin44cos44 alkalmazva), hogy
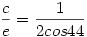
Ez viszont azt jelenti, hogy az EBC háromszög egyenlő szárú, azaz BE=c és B-nél az EBC-ben 92 fok van, felette 88 fok, így BOC háromszögben O-nál 85 fok, ami pontosan egyenlő a keresett szöggel, azaz  ui: O-val jelölve az AC és DB metszéspontját ui: O-val jelölve az AC és DB metszéspontját
Minden jót, Atosz!
|
 |
|
|
| [77] lorantfy | 2005-07-15 15:05:14 |
 Az ABC  köré írt körben A,B,C,E,G pontok biztos csúcsai a szabályos 180o-os sokszögnek. De mi garantálja, hogy F pont is az. A négyszög BD átlója nem biztos, hogy átlója a szab. sokszögnek. köré írt körben A,B,C,E,G pontok biztos csúcsai a szabályos 180o-os sokszögnek. De mi garantálja, hogy F pont is az. A négyszög BD átlója nem biztos, hogy átlója a szab. sokszögnek.
|
| Előzmény: [71] Hajba Károly, 2005-07-13 12:00:52 |
|
| [76] Lóczi Lajos | 2005-07-14 23:56:44 |
 Az Általad írt, megoldandó egyenlet az alábbi (ahol csc jelöli a koszekáns függvényt, azaz a szinusz reciprokát, és  -t fokokban keressük): -t fokokban keressük):
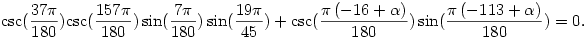
Az, hogy csak egyetlen megoldás van (180 fokonként), nevezetesen  =85, legegyszerűbben talán úgy látható be, hogy kiszámoljuk a bal oldal =85, legegyszerűbben talán úgy látható be, hogy kiszámoljuk a bal oldal  szerinti deriváltját, ami nem más, mint szerinti deriváltját, ami nem más, mint 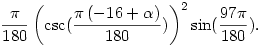 Erről viszont látszik, hogy mindig pozitív, a bal oldal tehát szigorúan monoton, így legfeljebb egy megoldás lehet, és beláttad, hogy a 85 jó is. Erről viszont látszik, hogy mindig pozitív, a bal oldal tehát szigorúan monoton, így legfeljebb egy megoldás lehet, és beláttad, hogy a 85 jó is.
|
| Előzmény: [75] Atosz, 2005-07-14 18:45:47 |
|
| [75] Atosz | 2005-07-14 18:45:47 |
 Szia!
Alapvetően igazad van, de nem volt kedvem az egyenlettel általánosságban bíbelődni. Egy teszt típusú feladatnál nyugodtan kipróbálhatjuk az értékeket, mert sok esetben hamarabb célhoz érünk. A felvázolt ábrából kitűnik, hogy itt a három esetből csak az egyik lehet jó. Kézenfekvő volt kipróbálni a 85 fokot, ami adta a megoldást. Ha hamis állítás jött volna ki, akkor azt néztem volna meg, hogy növelni, vagy csökkenteni kell-e a szöget egy epszilonnyival.
Minden jót, Atosz!
|
| Előzmény: [74] Lóczi Lajos, 2005-07-14 00:40:22 |
|
|
|
| [72] Atosz | 2005-07-13 12:34:14 |
 Sziasztok!
A 85 fokos feladatra találtam egy nem túl szép trigonometriai megoldást, ami alapján kijött, hogy a szög pontosan 85 fok!
Két viszonylag ritkán használt összefüggést használtam a szinusz-tétel mellett:
(1) 4sinxsinysinz=sin(x+y-z)+sin(y+z-x)+sin(z+x-y)-sin(x+y+z)
(2) 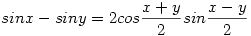
A lenti ábrán AC-t 1-nek véve felírtam két szinusz-tételt az oldalakra, majd AO-val a következő kettőt:
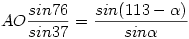
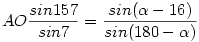
A kettőt elosztottam egymással, majd  helyére bepróbáltam a 85 fokot és átrendeztem, és kaptam hogy: helyére bepróbáltam a 85 fokot és átrendeztem, és kaptam hogy:
sin76sin7sin69=sin28sin37sin23
Alkalmazva (1)-et kapjuk, hogy
sin88-sin28=sin32
,majd (2)-t
2cos58sin30=sin32
ami viszont igaz, mert
cos58=sin32
Nem túl szép és nem is rövid, de kiadta a megoldást. Minden jót, Atosz!
|
 |
| Előzmény: [66] jonas, 2005-07-12 15:22:30 |
|
| [71] Hajba Károly | 2005-07-13 12:00:52 |
 Egyrészről a szabályos 180 szög bármely két csúcspontja a középpontból páros értékű szög alatt látszik, így bármely csúcs és a középpont egy másik csúcspontból nézve egész értékű szög alatt látszik. Mivel az átlók csúcstól csúcsig mennek, így bármely két átló által bezárt szög csak egész értékű lehet.
Másrészről egy csúcsból rendre egy-egy fok növekedéssel látható a következő csúcs, így 1-179 fok között minden szögérték előfordul. Így az átlók között 180 hasonló háromszögpárt tudunk találni.
HK
|
| Előzmény: [69] Kós Géza, 2005-07-12 21:14:20 |
|
|
| [69] Kós Géza | 2005-07-12 21:14:20 |
 A megoldás leírásával és lerajzolásával még adós vagyok. Most csak annyit segítek, hogy ha a szabályos 180-szög néhány átlója szerepel az ábrán.
|
| Előzmény: [66] jonas, 2005-07-12 15:22:30 |
|
| [68] Hajba Károly | 2005-07-12 16:21:55 |
 Én is csatlakozom.
CAD-del 85,0000 fokra jött ki, míg EXCEL-lel végiszámoltam, arányosítás, szögtételek és arkusz fv. 8 tizedes pontosságra beállítva kihozta a kerek szögértéket.
De hát ez sem bizonyítás csak valószínűség. Az erősített még, hogy a 15 pontos feladat könnyebb volt. :o)
HK
|
| Előzmény: [66] jonas, 2005-07-12 15:22:30 |
|
| [67] lorantfy | 2005-07-12 16:14:37 |
 Jogos a kérés! Én sem tudtam olyan geometriai indokot találni, ami bizonyította volna, hogy pontosan 85 fok. Számológéppel számolva természetesen nem jön ki pontosan. Ha egy szerkesztőprogram adja ki, hogy 85 fok, akkor sem biztos, hogy pontosan annyi, bizonyos mértékű kerekítés ott is be van építve.
|
| Előzmény: [66] jonas, 2005-07-12 15:22:30 |
|
| [66] jonas | 2005-07-12 15:22:30 |
 A 24. feladat megoldásához kaphatnék valami magyarázatot? Én kiszámoltam szögfüggvényekkel, és az jött ki, hogy elég nagy pontossággal 85 fok a szög, de nem tudom bizonyítani, hogy pontosan annyi. Igazából nem is értem, hogy jöhet ez ki pontos eredménynek. Először arra gondoltam, hogy ez egy húrnégyszög, de nem az.
|
|



 S-hez létezzen olyan r
S-hez létezzen olyan r


 n
n

 ui: O-val jelölve az AC és DB metszéspontját
ui: O-val jelölve az AC és DB metszéspontját 

 köré írt körben A,B,C,E,G pontok biztos csúcsai a szabályos 180o-os sokszögnek. De mi garantálja, hogy F pont is az. A négyszög BD átlója nem biztos, hogy átlója a szab. sokszögnek.
köré írt körben A,B,C,E,G pontok biztos csúcsai a szabályos 180o-os sokszögnek. De mi garantálja, hogy F pont is az. A négyszög BD átlója nem biztos, hogy átlója a szab. sokszögnek.