Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1924] Maga Péter	2014-05-29 21:55:21
Pach Peti e-mailben küldött nekem egy egyszerű ellenpéldát. Legyen &tex;\displaystyle b_1,b_2,b_3&xet; egy bázis. Legyen &tex;\displaystyle Ab_1=Ab_2=Bb_2=Bb_3=0&xet;, valamint &tex;\displaystyle Ab_3=Bb_1=b_2&xet;. Könnyű ellenőrizni, hogy minden ezekből alakuló másodfokú tag &tex;\displaystyle 0&xet;, tehát csak a &tex;\displaystyle cA+dB&xet; alakú polinomok jönnek szóba. Ezek meg nem jók, szintén könnyű ellenőrizni.
Előzmény: [1923] Maga Péter, 2014-05-18 16:46:11

[1923] Maga Péter

2014-05-18 16:46:11

Valaki mondja meg a következőt! Legyen &tex;\displaystyle A&xet; és &tex;\displaystyle B&xet; két lineáris transzformációja egy véges dimenziós valós vektortérnek. Van-e olyan polinomjuk, melynek konstans tagja &tex;\displaystyle 0&xet;, és a magtere éppen &tex;\displaystyle A&xet; és &tex;\displaystyle B&xet; magterének a metszete?

Nyilván minden (&tex;\displaystyle 0&xet; konstans tagú) polinom magtere tartalmazza &tex;\displaystyle A&xet; és &tex;\displaystyle B&xet; magterének metszetét. A cél tehát a fordított irányú tartalmazás elérése egy jól választott polinommal.

Előre is köszönöm.

[1922] Fálesz Mihály

2014-04-26 09:15:18

Egyszer egy elsőéves diákom mutatta be azt a hajmeresztő mutatványt, hogy egy &tex;\displaystyle f(x)^{g(x)}&xet; alakú kifejezést úgy derivált, hogy először kontansnak vette az alapot, deriválta, utána a kitevőt vette konstansnak, úgy is deriválta, majd a kétféle derváltat összeadta:

&tex;\displaystyle (f^g)' = (f^g \log f) \cdot g' + gf^{g-1}\cdot f'. &xet;

Először hüledeztem, hogy ezt lehet, de aztán megértettem, hogy csak a többváltozós láncszabályt alkalmazta. :-)

Például vegyünk két valós értékű egyváltozós függvényt, &tex;\displaystyle f&xet;-t és &tex;\displaystyle g&xet;-t, és legyen mindkettő differenciálható az &tex;\displaystyle a&xet; pontban. Deriváljuk a szorzatot az &tex;\displaystyle a&xet; pontban.

Legyen &tex;\displaystyle F\binom{x}{y}=xy&xet; és &tex;\displaystyle G(t)=\binom{f(t)}{g(t)}&xet;, ekkor tehát &tex;\displaystyle fg = F\circ G&xet;. A &tex;\displaystyle G&xet; differenciálható &tex;\displaystyle a&xet;-ban, és &tex;\displaystyle G'(a)=\binom{f'(a)}{g'(a)}&xet;, az &tex;\displaystyle F&xet; mindenhol differenciálható, és &tex;\displaystyle F'\binom{x}{y}=(y,x)&xet;. A láncszabály szerint &tex;\displaystyle F(G(t))=f(t)g(t)&xet; is differenciálható &tex;\displaystyle a&xet;-ban és

&tex;\displaystyle (fg)'(a) = (F\circ G)'(a) = F'(G(a)) G'(a) = (g(a),f(a)) \binom{f'(a)}{g'(a)} = g(a)f'(a) + f(a)g'(a). &xet;

A dolog persze csalás, mert a többváltozós differenciálási szabályokat jóval az alapműveletek differenciálása után építjük fel (kb. olyan, mint amikor valaki a koszinusz-tételből vezeti le a Pitagorasz-tételt), de mindenképpen érdekes.

Előzmény: [1921] marcius8, 2014-04-25 16:30:39

[1921] marcius8	2014-04-25 16:30:39
Állítólag a differenciálási szabályok (függvények lineáris kombinációjának deriváltja, függvények szorzatának deriváltja) levezthetőek az összetett függvényekre vonatkozó differenciálási szabályból (láncszabály). Vajon hogyan történik mindez? Tisztelettel: Bertalan Zoltán.

[1920] mihtoth	2014-02-11 07:56:37
Köszönöm a segítséget!
Előzmény: [1911] n, 2014-02-10 18:19:39

[1919] Lóczi Lajos

2014-02-10 23:04:30

Illetve

195.96043078097043710<a₁₂₀₀₁<195.96043078097043711.

Előzmény: [1918] Lóczi Lajos, 2014-02-10 22:55:00

[1918] Lóczi Lajos	2014-02-10 22:55:00
Ha a₁=120, akkor 195.95532757702918725<a₁₂₀₀₀<195.95532757702918726.
Előzmény: [1912] Fálesz Mihály, 2014-02-10 19:17:42

[1917] Róbert Gida	2014-02-10 22:39:21
a_n $\ge$ b₁^{2^n-1} majdnem trivi, ha b₁>0 egész: legyen ugyanis $b_n=\frac {p_n}{q_n}$ , ahol lnko(p_n,q_n)=1. Ekkor $b_{n+1}=b_n+\frac{1}{b_n}=\frac{p_n}{q_n}+\frac{q_n}{p_n}=\frac{p_n^2+q_n^2}{p_nq_n}$ , de ez a tört már tovább nem egyszerűsíthető, hiszen lnko(p_n,q_n)=1volt, így a_n+1=p_n²+q_n²=a_n²+q_n²>a_n² $\ge$ b₁^2ⁿ (ez utóbbi teljes indukcióval).
Előzmény: [1916] Róbert Gida, 2014-02-10 22:05:38

[1916] Róbert Gida

2014-02-10 22:05:38

a_n az pont b_n számlálója, így egész, azaz két egész szám közé nem eshet. És valószínűleg sokkal nagyobb.

T(n)=2^{3.453495382*2ⁿ} egy valószínűleg jó becslés a kérdésre (kiinduló tag=b₁=120). Egyébként már a₂₅-nek 34883379 számjegye van.

Előzmény: [1912] Fálesz Mihály, 2014-02-10 19:17:42

[1915] Lóczi Lajos	2014-02-10 21:22:16
Lásd még az "ujjgyakorlatok" [420]-as hozzászólását 2005-ből.
Előzmény: [1912] Fálesz Mihály, 2014-02-10 19:17:42

[1914] n	2014-02-10 19:21:14
(Illetve most másodjára számoltam el. Tényleg fáradt vagyok, szóval duplán kéretik ellenőrizni a hozzászólásomat felhasználás előtt.)
Előzmény: [1913] n, 2014-02-10 19:19:26

[1913] n	2014-02-10 19:19:26
(Naná, hogy elszámoltam, nem a 12000. tagot számoltattam ki.)
Előzmény: [1911] n, 2014-02-10 18:19:39

[1912] Fálesz Mihály

2014-02-10 19:17:42

A sorozatnak a négyzetét érdemes vizsgálni. Ha b_n=a_n², akkor

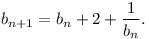
$b_{n+1} = b_n+2+\frac1{b_n}.$

Ebbből egy sor, egyre erősebb alsó és felső becslést lehet kapni, pl.

b_n $\ge$ b₀+2n

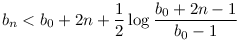
$b_n < b_0+2n+\frac12\log\frac{b_0+2n-1}{b_0-1}$

A Te esetedben b₀=120²=14400 és n=12000, tehát

38400<b_{_n}=a_n²<38400,5

195,959<a₁₂₀₀₀<195,961.

Előzmény: [1911] n, 2014-02-10 18:19:39

[1911] n	2014-02-10 18:19:39
Pontos, nem rekurzív, nem végtelen szummás általános képletet nem írtak, csak közelítőt, szóval ha pontosan kell, akkor szerintem célszerű a speciális esetekre programot írni. (A konkrét példára, ha minden igaz, 195.9604307809704, ha a 120 a nulladik tag, ha az első, 195.95532757702915.) Egy becslés, ha jól értelmeztem (nem teljesen biztos, kissé fáradt vagyok): *___1 kezdőértékű___ ilyen sorozatra e^2b(n)²-4n/n tart egy konstanshoz (0.574810274671785...), ahol b(n) a sorozat. Ahogy néztem, azt eltérés, ha az első érték az 1, a 10. elemre -0.010916374964937692, a 100.-ra -0.004394777829750618, az 1000.-re -0.0007695696146290398, a 10000.-re -0.0001100303693110094 (itt már kerekítési hibák is felléphettek, sima floating point számokkal dolgoztam lustaságom miatt).
Előzmény: [1910] mihtoth, 2014-02-10 15:32:01

[1910] mihtoth

2014-02-10 15:32:01

Köszönöm!

De az a baj, hogy én az ott leírtakon nem bírtam eligazodni.

Mennyi egy ilyen sorozat 12000-ik elemének értéke, ha a kezdőérték 120?

Üdv: mihtoth

Előzmény: [1909] jonas, 2014-02-10 13:43:41

[1909] jonas	2014-02-10 13:43:41
Lásd A073833, ami ad egy közelítő képletet.
Előzmény: [1908] mihtoth, 2014-02-10 13:11:29

[1908] mihtoth	2014-02-10 13:11:29
Adott az alábbi rekurzió: a(n+1)=a(n)+1/a(n) Hogyan lehet megadni az n-ik tag kiszámításának képletét, ha ismerjük az első tagot?

[1907] HoA

2013-11-05 16:07:53

A "működés" magyarázata az, hogy ha egy négyjegyű N számról megállapítom, hogy egy 10k szám négyzeténél nagyobb, akkor valamilyen (10k+x) négyzete lesz vagy nagyobb, N $\ge$ 100k²+20kx+x² . Levonva k² -et N-100k² $\ge$ 20kx+x²=(20k+x)x Amikor a "72 alá írom és levonom a 64-et és leveszem a következő két számjegyet", akkor tkp. 7225 - ből vonom ki a 6400-at. Ennek kell egyenlőnek ( vagy nagyobbnak ) lenni mint (20k+x)x , vagyis (160+x)*x. Több jegyre a gondolatmenet folytatható.

A leíráshoz két javítás:

Nem balról jobbra, hanem jobbról balra kell kettes csoportokra osztani a szám jegyeit. Páros számú számjegynél, mint itt is, mindegy, de 37225 négyzetgyökének számítását nem a 37-tel kell kezdeni, hanem 3-mal.

A "mutató" keresése úgy hogy letakarom az utolsó számot, csak tájékoztató, nem biztos hogy megfelel. Például ha egy számításban odáig jutok, hogy 815:16x*x -et kell vennem, akkor a letakarás [81/16] = 5-öt ad, de 165*5 > 815, tehát csak 4-et vehetek.

Előzmény: [1906] epszi, 2013-11-04 21:07:18

[1906] epszi

2013-11-04 21:07:18

Az lenne a kérdésem, hogy miért működik ez a gyökvonásos trükk? 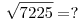$\sqrt{7225}=?$ (ezt a változatot az internet bugyraiból kerestem, de magát a módszert Arthur Benjamin Fejszámolás c. könyvében olvastam.)

7225 négyzetgyökének kiszámítása papíron:

Balról jobbra haladva veszem az első két számot és megnézem melyik az a legnagyobb szám amelynek a négyzete megvan a hetvenkettőben.

72'25=

Az a szám a 8 mert 8-nak a négyzete 64 . Leírom az egyenlőség jel után a 8-t és leírom a hetvenkettő alá a 8 négyzetét (64).

72'25=8 64 A 64-et kivonom a 72-ből és leveszem a következő két számjegyet.

72'25=8 (hányados) 72'25=8 (hányados) 64 64 08 (maradvány) 825

A kapott számjegyet ( 825) elosztom a hányados kétszeresével (16) úgy, hogy letakarom az utolsó számjegyet (5-t) és megnézem hányszor van meg a kapott értékben (82-ben). Ahányszor megvan az lesz a hányados mutatója. A mutató az öt lesz, mert 82-ben a tizenhat megvan 5-ször. 72'25=8 64 825:16 (82:16=5)

A hányados mutatót leírom a hányados kétszerese után (165 lesz) és ezt az értéket megszorzom a hányados mutatójával (5). 72'25=8 72'25=8 64 64 825:16 825:165*5

A kapott értéket kivonom a maradványból(825). Ha a szorzat értéke az a legnagyobb szám amely még megvan a 825-ben, akkor A hányados mutató értékét felírom a hányadosba.

72'25=85 Tehát a 7225- nek a négyzetgyöke 85 64 825:165*5 ( 165*5=825) 825 000 Ha a maradék nem nulla, akkor a hányadosban kiteszem a tizedesvesszőt és leveszem a következő két számot.

[1905] Viking	2013-10-14 17:24:08
Nagyon jó példa, köszönöm szépen!
Előzmény: [1904] n, 2013-10-14 17:12:13

[1904] n	2013-10-14 17:12:13
Legegyszerűbb cáfolat: a csupa 5-ös négyzetre 45 az összeg, de mégse szabályos a sudokuban. És ugyebár 1 ellenpélda tökéletesen elég az állítást cáfolni.
Előzmény: [1903] Viking, 2013-10-14 16:43:09

[1903] Viking

2013-10-14 16:43:09

Sziasztok!

Matematikus gondolkodással ki, hogyan tudja igazolni vagy cáfolni... Egy 9x9-es sudoku tábla helyes kitöltéséhez elegendő feltétel-e, hogy minden sor, minden oszlop, illetve minden egyes "kis" négyzet esetén igaz, hogy a benne lévő számjegyek összege 45?

[1902] w

2013-10-13 20:30:14

1. $y=\frac{2x+3}{4x+5}$ --> 4xy+5y=2x+3, x(4y-2)=3-5y, $x=\frac{3-5y}{4y-2}$ . Tehát $f^{-1}(x)=\frac{3-5x}{4x-2}$ . Kérdés, hogy mi az értelmezési tartomány?

2. Emeld az első egyenletet $\frac1{\sqrt y}$ -odik hatványra, majd helyettesíts a második egyenletbe.

3. A második egyenletből megkapod x+y-t, fejezd ki y-t, majd írd bele az elsőbe.

Előzmény: [1901] koma, 2013-10-13 19:30:11

[1901] koma

2013-10-13 19:30:11

Sziasztok,

ha valaki tud, kérem segítsen az alábbi feladatok megoldásában:

1, az alábbi függvények mi az inverze ?: 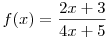$f(x)= \frac{2x+3}{4x+5}$

2, Oldjuk meg a következő egyenletrendszert:

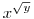$x^\sqrt y$ =y

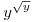$y^\sqrt y$ =x⁴

3, Oldjuk meg a következő egyenletrendszert:

64^2x+64^2y=12

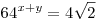
$64^{x+y} = 4 \sqrt 2$

Köszönöm szépen a segítséget

[1900] Inverz	2013-10-11 19:40:39
Köszönöm a segítséget!

Már regisztráltál?
Új vendég vagy?