| [500] epsilon | 2008-05-02 08:33:38 |
 Kedves Káli gúla! Köszi, hogy foglalkozol a problémával, és általánosítottabb formában elsőfokú föggvénnyel próbáltad asszimptótikusan megközelíteni az integrandusz alatti függvényt. Megpróbáltam emésztgetni a leírtakat, de amikor az utolsó integrálhoz értem, vagyis amit lennebb beteszek, ahoz, hogy ott a limesz 1/2 legyen szükséges a k1=k2=2...és akkor az azelőtt levő x+e(expx) közrefogása egy egyenlőségé alakúlnak, ami nem igaz. Ha tévedek,vagy rosszul értettem valamit, légyszíves javíts ki, mert a feladat megoldása ami érdekel, nem az, hogy keressem a kákán a csomót...de úgy látom, hogy..ahol jeleztem, elakadtam. Előre is kösz, üdv: epsilon
|
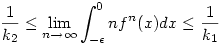 |
| Előzmény: [499] Káli gúla, 2008-05-01 23:13:41 |
|
|
| [498] epsilon | 2008-04-30 08:24:11 |
 Nagyszerű nadorp! Ez volt az egyetlen transzformáció ami változatlanul hagyta a nevezőt és a számlálóval is volt mit kezdeni. Természetesen a mezei integrál 4/4-el szorozva, azonnal kijön. Köszi szépen, ez sem volt piskóta, még maradt a 731. amire kiváncsi vagyok, megint egyedi-e a megoldása. A felygyült integráltesókat szerencsére ritkítottam, de ezek keményebb diók voltak Üdv: epsilon
|
| Előzmény: [497] nadorp, 2008-04-29 21:06:23 |
|
|
|
| [495] epsilon | 2008-04-29 13:57:56 |
 Ha segítene valamit, a 731.-nek a limesz értéke 1/2, próbáltam még Taylor sorral, az sem jött össze, a Newton Binomiális képlet az nem dobja ki az 1/2-öt, tehát ha azzal próbálom, valami összeg limeszeként kellene előálljon, de még mindig a rekurzióval próbálkozom, akár másodrendű is jó lenne...A 736-ot is a 735 mintájáta analóg változcserével, nem alakult úgy egyenlenek, mint a 735, a nevező megváltozott :-(
|
|
| [494] Sirpi | 2008-04-29 10:03:01 |
 Na ezt gondold át még egyszer :-) A függvény primitív függvénye valóban csak konstans erejéig meghatározott (legyen F(x)+c), de mivel rögzített intervallumon integrálunk, ezért az integrál értéke pl. az első esetben F(0)+c-F(-1)-c=F(0)-F(-1) teljesen független a konstans megválasztásától - ami nem is csoda, mert az integrál megegyezik ezen az intervallumon a görbe alatti területtel.
|
| Előzmény: [493] Róbert Gida, 2008-04-29 08:57:50 |
|
| [493] Róbert Gida | 2008-04-29 08:57:50 |
 Az első és az utolsó limesz persze csak úgy értelmes, hogy az integráloknál az integrációs konstans mindig 0, különben a limesz nem létezik, hiszen csak konstans erejéig meghatározott az integrál.
|
| Előzmény: [492] epsilon, 2008-04-29 06:44:10 |
|
| [492] epsilon | 2008-04-29 06:44:10 |
 A 731.-hez ha Valaki egy rekurziós öszefüggést tudna megállapítani, az is elég lene...
|
|
| [491] epsilon | 2008-04-28 16:18:35 |
 A 735. is hosszas ütközetek után kinyírva, az x=(2-t)/(1+2t) változócserével egy kiszámítható, meg az eredeti integrál ellentettje lett. Szóval ez sem volt piskót! Még maradt 2, de közben megint gyűlt vagy 10 :-(
|
|
| [490] epsilon | 2008-04-28 15:18:50 |
 Elnézést, a 731. feladatban a KÜLSŐ 2 helyett van az n (nem belül, ott e az x hatványon van), amásik esetben úgy van, ahogyan jonas kihangsúlyozta!
|
|
|
|
| [487] epsilon | 2008-04-28 09:50:50 |
 A 734. meglett :-) , szép feladat!
|
|
| [486] epsilon | 2008-04-27 10:37:40 |
 Helló!Megint gyűltek keményebb feladatok, a következő integrálok esetén sorra valahol belefulladtam, vagy regény lett a megoldásból :-( ha Valakinek van valami örlete, előre is köszönöm! Üdv: epsilon
|
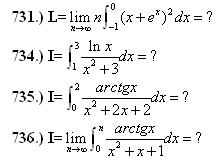 |
|
| [485] epsilon | 2008-04-25 14:30:03 |
 Hát akkor ezek szerint, a több mint 1000 feladatot tartalmazó könyvből kb ez a 3. hibás (hiányos megfogalmazásu,) feladat.
|
|
| [484] nadorp | 2008-04-24 09:52:46 |
 Ekkor Doom megoldását általánosítva k<m<n pozitív egészekre a
qn-(4k+1)qm+(5m-n)qk+(4k-5m+n)=0
egyenletnek kell keresni az összes q 1 valós megoldását. Kérdés, hogy mindig van-e? 1 valós megoldását. Kérdés, hogy mindig van-e?
Pld. k=1 m=2 n=4 esetén q2+2q-2=0 vagy
k=1 m=3 n=5 esetén q3+2q2-2q-6=0
|
| Előzmény: [483] epsilon, 2008-04-23 15:54:54 |
|
| [483] epsilon | 2008-04-23 15:54:54 |
 Helló Doom! Úgy fordítottam, és ez alapján úgy értem, hogy mindkét sorozatból összeadjuk pl. az m-edik, n-edik, p-edik, s-edik tagokat, ahol az m, n, p, s nem föltétlen egymás utáni számok.
|
| Előzmény: [482] Doom, 2008-04-23 15:32:13 |
|
|
| [481] epsilon | 2008-04-23 14:47:55 |
 Helló Doom és Csimby!A feladat fordításból származik, többször is átnéztem, de SEHOL sem ír arról, hogy EGYMÁSUTÁNI tagok lennének, úgy írja, hogy 4 azonos (egyforma) sorszámú (indexű) tagok páronkénti öszegéről van szó! Sajnos ebben az esetben nem látom be a Káli gúla szép megoldásában, hogy az úgy lenne :-( és olyan kár lenne érte :-(
|
| Előzmény: [473] Doom, 2008-04-22 07:31:52 |
|
| [480] Sirpi | 2008-04-23 11:20:34 |
 Köszi a válaszokat! Akkor nem is agyalok tovább rajta :-)
|
|
| [479] HoA | 2008-04-22 17:54:24 |
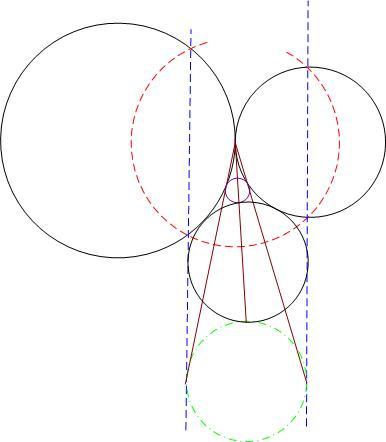
 Én is. De ha már lerajzoltam, felteszem a szerkesztés megoldását. Inverzióval egyszerű. Legyen az inverzió középpontja a két nagyobb - ha van - kör ( k1 és k2 ) érintési pontja, alapköre pedig a harmadik körre ( k3 )merőleges. ( piros kör ). Ekkor k3 inverze önmaga, a másik kettőé két párhuzamos, k3-at érintő egyenes (kék) . A szerkesztendő kör inverze érinti k3-t és a két egyenest (zöld). A szerkesztendő érintési pontokat a zöld kör érintési pontjainak az inverzió középpontjából történő vetítésével kapjuk (barna egyenesek).
|
 |
| Előzmény: [478] jonas, 2008-04-22 16:41:19 |
|
|
|
|


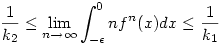

 esetén |f(x)|<h<1, és így a (-1,-
esetén |f(x)|<h<1, és így a (-1,- 0-val lehet felülről becsülni. Lineáris függvényekre könnyen kiszámolhatjuk az integrált -
0-val lehet felülről becsülni. Lineáris függvényekre könnyen kiszámolhatjuk az integrált - f(x)
f(x)


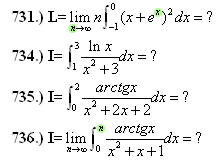

 , ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.
, ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.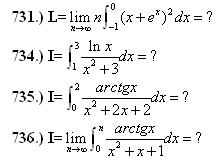
 1 valós megoldását. Kérdés, hogy mindig van-e?
1 valós megoldását. Kérdés, hogy mindig van-e? 

