| [728] j.milan | 2008-12-30 22:14:13 |
 Jóestét! Az én problémám az, hogy van két egyenes egyenlete, amik elképesztően ronda paraméteres alakban vannak, és elvileg merőlegesek egymásra. A merőlegesség bizonyítására szeretnék kérni egy egyszerűbb ötletet, ha létezik, amiben nagyon bízom
|
|
| [727] Bormann | 2008-12-26 23:06:48 |
 Mindenkit üdvözlök! Most volt az osztályban karácsonyi ajándékozás, és kissé elgondolkoztam azon, hogy mekkora az esélye ezzel kapcsolatban egyes dolgoknak. Pl. annak, hogy egy kör van az osztály gráfjában(azaz, ha A átadja B-nek az ajándékot, B C-nek és így tovább, akkor az utolsó ember éppen A-nak ad ajándékot és közben sem szakad meg a sor.) Abban az esetben, ha valaki kihúzhatja magát, akkor nem nehéz ennek a valószínűsége, de nálunk senki sem húzhatja magát, és ez az eset már bonyolultabb, rajtam egyelőre kifogott. Minden hozzászólást örömmel fogadok, akár más valószínűséggel kapcsolatban is, pl., hogy mekkora valószínűséggel van az osztály gráfjában 1, 2, 3, ..., 16 kör(32-en vagyunk, és mivel senki sem húzhatja magát, ennél nem lehet több kör). Előre is köszönöm!
|
|
|
| [725] Gyöngyő | 2008-12-26 20:31:39 |
 Sziasztok!
azt szeretném megkérdezni,hogy hogyan látható be pl.hogy a Lip(alpha) nem homogén Banach tér?
Üdv:
Gyöngyő
|
|
| [724] epsilon | 2008-12-20 11:24:27 |
 Tisztelt Kollégák! A maradékosztályok modulon halmazon értelmezett + és × által képezett (Z(n), +, ×) gyűrűn szeretném tárgyalni az ax+by=c Diofantikus, az elsőfokú 2 ismereltenes 2 egyenletből álló, valamint az elsőfokú 3 ismeretlenes 3 egyenletből álló egyenletrendszerek megoldhatóságát. Tudna-e Valaki valamilyen netes információt adni, vagyis linket adni, ahol ezekről olvashatok, magyar, francia vagy angol nyelven. Előre is köszönöm, üdv: epsilon
|
|
|
|
| [721] Ágoston | 2008-12-08 17:56:55 |
 A mostani kömal B. 4122.ben "A piros mezők közül kettő a tábla szélén van". Ez azt jelenti, hogy legalább kettő, vagy azt, hogy pontosan kettő?
|
|
| [720] HAnonymus | 2008-12-07 20:29:07 |
 Köszi a segítséget, megnyugodtam. :)
|
|
| [719] leni536 | 2008-12-07 16:07:05 |
 A differenciálegyenletet jól írtad fel, a megoldásodat visszaírva kielégíti a differenciálegyenletet és a kezdeti feltételeket is, megvan a két szabadsági fok is, úgyhogy jó valószinűleg. Erre a típusú diffegyenletre mi v(x)-et kerestük és vezettük vissza vele elsőfokúakra, azzal is ez jön ki.
|
| Előzmény: [718] HAnonymus, 2008-12-04 13:39:06 |
|
| [718] HAnonymus | 2008-12-04 13:39:06 |
 Sziasztok!
Egy differenciálegyenletes feladatban szeretnék segítséget kérni.
A következő lenne: Egy 6 m hosszú lánc súrlódás nélkül csúszik az asztalon. Ha a csúszás akkor kezdődik, amikor már 1m-nyi lánc lóg lefelé, akkor mennyi idő múlva esik le a lánc? (Feltesszük, hogy az asztal legalább 6 m magas lábakon áll.)
Ötletem az van rá, csak szerintem hibás a gondolatmenetem, szívesen venném ha valaki véleményezné.
Abból indulok ki hogy leesésnek az számít amikor az utolsó láncszem is lefut az asztalról.
Sajnos TeX-használatban nem állok sehogy, úgy találtam egyszerűnek a dokumentálását ha képként elmentem azt ahogy megoldottam, és felteszem egy tárhelyre: ide
Örülnék ha valaki véleményezné, vagy akár teljesen máshogy megoldaná. Köszönöm előre is a segítséget.
Üdv: egy ZH-ra készülő amatőr. :)
|
|
|
|
| [715] leni536 | 2008-12-02 21:07:02 |
 "Érezhető", hogy ha egy konvex síkidom magába foglal egy nála kisebb konvex síkidomot, akkor a külső síkidom kerülete nagyobb, mint a másik síkidom kerülete. Létezik erre tétel? Van erre közismert bizonyítás?
|
|
| [714] Euler | 2008-11-30 19:53:29 |
 Az eredményt konkrétan nem mondom meg, mert nem számoltam végig, de az eljárás a következő:a nevezőben ird fel a nevezetes szorzatot, majd bonts parciális törtekre, ennek módszere több helyen is megtalálható, pl. Bárczy Barnabás: Integrálszámitás c. könyvében is. Innen már "könnyű" a feladat, remélem elég segitséget adtam a feladat megoldásához.
|
| Előzmény: [711] sandor720, 2008-11-29 17:28:56 |
|
| [713] sandor720 | 2008-11-30 12:40:14 |
 Szia!
A mapel-re gondoltál Robert Gida? Az ha jóltudom nem vezeti le csak a megoldást mutatja meg!
|
|
|
| [711] sandor720 | 2008-11-29 17:28:56 |
 Köszönöm a segitséget! Vola itt még egy feladat
|
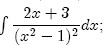 |
|
|
|
| [708] sandor720 | 2008-11-29 13:36:32 |
 sziasztok!
Köszönöm a segitségeteket integráláshoz nem tudom levezetni melyik szabály alkalmazható a:
|
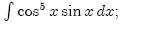 |
|
| [707] Gyöngyő | 2008-11-26 21:21:24 |
 Szia!
Amit csináltam megoldást az pontosan az amit most leirtál. Azt mondta rá a tanárom,hogy szerinte sincs egyszerűbb megoldás.Majd megprobálom feltölteni a megoldásomat,ha sikerül,csak most ezzel a konvex geometriai feladattal szenvedek.
Üdv.: Gyöngyő
|
| Előzmény: [706] sakkmath, 2008-11-26 18:54:21 |
|
| [706] sakkmath | 2008-11-26 18:54:21 |
 Kiegészítés: A (2) egyenlőtlenség bal oldalán álló kifejezés t-nek páros függvénye, ezért elég az egyenlőtlenséget t 0-ra bebizonyítani. Ekkor az alkalmazott 0-ra bebizonyítani. Ekkor az alkalmazott 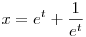 helyettesítés már egy-egy értelmű megfeleltetést létesít az x-ek t-k halmaza között, hiszen az x(t)=2cht függvénynek csak az első síknegyedbe eső, szigorúan monoton növekedő részével van dolgunk. helyettesítés már egy-egy értelmű megfeleltetést létesít az x-ek t-k halmaza között, hiszen az x(t)=2cht függvénynek csak az első síknegyedbe eső, szigorúan monoton növekedő részével van dolgunk.
Egy kérdés Gyöngyőhöz: Születtek-e a feladatra más, egyszerűbb megoldások?
|
| Előzmény: [654] sakkmath, 2008-10-31 17:17:06 |
|
| [705] Gyöngyő | 2008-11-26 16:27:58 |
 Sziasztok! Az alábbi két feladathoz szeretnék segítséget kérni:
1.:Vesszük az összes konvex centrálszimmetrikus sokszöget.Az a kérdés hogy milyen határok között változik a kerülete,ha a saját normájában nézzük.Pl. ha a négyszöget nézzük akkor a négyszög normában mekkora a kerülete.
2.:Mekkora az azonos centrumú szabályos n-szög és kör Hausdorf távolsága?
Köszi elöre is. Gyöngyő
|
|
|



 =2. Ekkor az f(x)=x2 (x
=2. Ekkor az f(x)=x2 (x I) függvény Lipschitz-folytonos,
I) függvény Lipschitz-folytonos,  f már nem tartozik ebbe az osztályba, ha
f már nem tartozik ebbe az osztályba, ha 



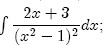

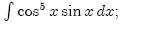

 0-ra bebizonyítani. Ekkor az alkalmazott
0-ra bebizonyítani. Ekkor az alkalmazott