| [653] enyac | 2008-10-23 04:40:17 |
 Köszönöm szépen a segítséget, sikerült a zh-m! :-)
|
|
| [652] nadorp | 2008-10-20 14:18:55 |
 Természetesen alkalmazható, ezt nem is vitatom, (sőt még a végeredmény is meg fog egyezni :-), csak nekem mindig "hasogassa" a szememet :-) ha mezei deriválás helyett nagyágyút - L'Hospital-t használunk.
|
| Előzmény: [651] jenei.attila, 2008-10-20 11:46:56 |
|
|
| [650] nadorp | 2008-10-20 08:51:48 |
 Csak egy megjegyzés:
Ha g(x)=log2(x+2), akkor a feladat g'(0) értékét kérdezi, úgy hogy itt szerintem a L'Hospital szabály nem "való" ( ahogy a 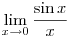 esetén sem), mivel a logaritmus deriváltjának meghatározásakor épp ezt a határértéket használjuk fel. esetén sem), mivel a logaritmus deriváltjának meghatározásakor épp ezt a határértéket használjuk fel.
|
| Előzmény: [646] enyac, 2008-10-19 19:08:01 |
|
|
|
| [647] S.Ákos | 2008-10-19 20:09:41 |
 Vizsgáljuk külön-külön a számláló és a nevező határértékét:
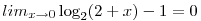
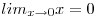
Mivel a határérték 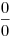 alakú, így az L'Hospital szabály alapján : alakú, így az L'Hospital szabály alapján :
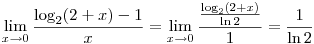
(remélem nem szúrtam el semmit)
|
| Előzmény: [646] enyac, 2008-10-19 19:08:01 |
|
| [646] enyac | 2008-10-19 19:08:01 |
 Köszönöm szépen a segítséget! Lenne még egy feladat, amiben nagyon sürgősen szükségem lenne segítségre (legkésőbb holnap reggelig) - nagyon szépen kérem, segítsetek, talán ezen múlik a zh-m...
Íme:
|
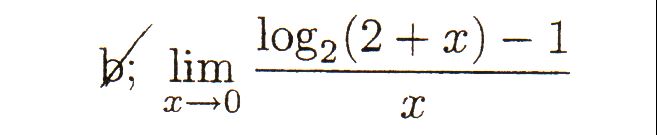 |
| Előzmény: [645] Lóczi Lajos, 2008-10-18 15:11:42 |
|
|
|
| [643] enyac | 2008-10-18 13:10:17 |
 Üdv!
Egy rövid kérdés: hol folytonos a sin x függvény egészrésze? Ahol nem folytonos, ott folytonossá tehető?
|
|
|
| [641] sanyikavagyok | 2008-10-12 21:39:11 |
 van egy házim amivel nem tudok mit kezdeni, mivel nem nagyon vagyok jó matekból, de azt is kell tanulnom:) segítenétek?
|
|
| [640] gmaccone | 2008-10-10 02:32:10 |
 Hello!
szerintem ha elkezded kibontani a rekúrziót akkor kapsz egy ilyet, hogy:
t(n)<=n+an+bn+t(a2n)+2t(abn)+t(b2n)<=...
(feltéve, hogy kommutatív számkörben operálunk:-)
végül:
t(n)<=n+n(a+b)+n(a+b)2+...+n(a+b)k+...
mértani sor összegképlet alapján LINEÁRIS BECSLÉST akkor tudsz adni, ha abszolút érték a+b<1 ugyanis akkor n/(1-(a+b))-vel tudod becsülni, de lehet, hogy én félreértettem a feladatot.
Peace
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|
|
| [638] Doom | 2008-10-08 18:40:21 |
 Szia!
Nem szép dolog egy pályázat feladatát megoldani helyetted, úgyhogy inkább csak egy kis támpontot adnék:
- A teljesítmény mértékegysége a watt (W), ami az időegység alatt végzett munka, azaz W=J/s.
- Ehhez az időt tudod (1 óra 10 perc), a benzin sűrűségéből és térfogatából meg tudod kapni a tömegét (m=V* ), abból pedig az égéshő segítségével az összes munkát. A hasznos teljesítmény az összes munka szorozva a hatásfokkal. És ekkor már majdnem készen is vagy... ), abból pedig az égéshő segítségével az összes munkát. A hasznos teljesítmény az összes munka szorozva a hatásfokkal. És ekkor már majdnem készen is vagy...
- Ügyelj a mértékegységekre!
|
| Előzmény: [637] Dorottya, 2008-10-08 15:58:24 |
|
| [637] Dorottya | 2008-10-08 15:58:24 |
 Szolnokról autóval mentünk Csongrádra. A 90km-es utat 1 óra 10 perc alatt tettük meg. Az autó közben 6 liter benzint fogyasztott. A benzin sűrűsége 700 kg/köbméter, égéshője 46000kJ/kg. A motor hatás foka 40 százalék. Mekkora a motor hasznos ( tényleges) teljesítménye? Lécci segítsetek pályázatot írok és 14pontos feledat de még nem tanultuk. Köszönöm szépen.
|
|
| [636] Lóczi Lajos | 2008-10-07 22:06:01 |
 Szerintem ha egy változó elé nem teszünk kvantort, akkor a szokásos értelmezésben mindig "minden" kvantort értünk elé.
"Bizonyítsuk be, hogy n>1 esetén..." ezalatt szerintem mindenki azt érti, hogy "minden n>1 esetén" stb.
|
| Előzmény: [633] sakkmath, 2008-10-07 19:05:05 |
|
| [635] Gyöngyő | 2008-10-07 19:48:46 |
 De ha vkit érdekel a feladat megoldása,annak elküldöm. Mindekettő feladatot megoldottam!
Üdv.: Zsolt
|
|
| [634] Gyöngyő | 2008-10-07 19:45:26 |
 Sziasztok!
Nem is tudtam hogy ezek a feladatok valahol le vannak közölve! Nekem van egy órám,az egyenlötlenségek,és ott kapjuk ezeket a feladatok Pintér Lajos tanár úrtól. Akkor addig nem kell válaszolni a monthly-s feladatra, a másik feladat ami szerintetek a magazinba van,az is ott kaptuk de arra van megoldásom! Nem tudom hogy az meddig él,majd utánna beirom ide!:-)
Köszike még1szer!
Üdv.: Gyöngyő
|
|
| [633] sakkmath | 2008-10-07 19:05:05 |
 A kétféle megfogalmazás között szerintem van különbség, s ezt egy egyenlőtlenség két szövegváltozatán próbálom bemutatni:
Gyöngyő-féle szövegezés:
2x 3x ahol x 3x ahol x 0. 0.
Donald Knuth-féle szövegezés:
Bizonyítsuk be, hogy az összes nemnegatív x-re 2x 3x. 3x.
A Gyöngyő-féle példafeladatnak van megoldása, s ez az x=0, ezzel szemben a Knuth-féle példafeladat állítása egy hamis állítás. (A Gyöngyő-féle szövegezés nem minden nemnegatív x-re írja elő az egyenlőtlenséget, míg a Knuth-féle szöveg minden nemnegatív x-re előírja ezt az egyenlőtlenséget.)
|
| Előzmény: [632] Lóczi Lajos, 2008-10-07 16:10:00 |
|
|
| [631] sakkmath | 2008-10-07 11:40:12 |
 Szia! Ez a feladat a The American Mathematical Monthly 2008/júniusi számában jelent meg azzal a "kis" különbséggel, hogy az egyenlőtlenséget az összes valós t-re és az összes   2-re kell bebizonyítani. 2-re kell bebizonyítani.
A megoldásokat a Monthly 2008. október 31-ig kéri a nyomtatott lapban közölt címre. Ez arra utal, hogy (üzleti okokból) elsősorban a lap vásárlóitól várják a megoldásokat. Ezek miatt úgy vélem, az lenne a helyes, ha az esetleges megoldó csak november 1-től tenné nyilvánossá a megoldását bárhol, s így pl. itt, a Fórumban is. Alább mellékelem az interneten talált, idevágó laprészletet.
(Az Érdekes matekfeladatok [2727]-es hozzászólásában általad közölt feladat szintén "él" és egy másik matematikai MAGAZIN várja a megoldását 2008. november 1-ig.)
Üdvözlettel: sakkmath
|
 |
| Előzmény: [602] Gyöngyő, 2008-09-28 13:55:06 |
|
|
| [629] Róbert Gida | 2008-10-06 22:51:05 |
 Nem írtad, de feltételezem, hogy T a természetes egészeken van értelmezve, így a,b 0-t is feltehetem. 0-t is feltehetem.
1. eset: a+b<1. Tetszőleges N0 egészre és elég nagy d számra telejesül, hogy T(n) d*n minden n<N0-ra. Legyen most d*n minden n<N0-ra. Legyen most 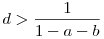 és még olyan nagy, hogy az előbbi feltétel is teljesül, azaz T(n)<d*n, ha n<N0 és még olyan nagy, hogy az előbbi feltétel is teljesül, azaz T(n)<d*n, ha n<N0
Indukcióval tegyük fel, hogy k<n-re T(k) d*k. Ekkor k=n-re is teljesül ez: a feltételt használva: T(n) d*k. Ekkor k=n-re is teljesül ez: a feltételt használva: T(n) n+T(an)+T(bn) n+T(an)+T(bn) n+adn+bdn=(1+d(a+b))n n+adn+bdn=(1+d(a+b))n dn teljesül, mert d(1-a-b)>1 igaz, d-re tett feltevés miatt. dn teljesül, mert d(1-a-b)>1 igaz, d-re tett feltevés miatt.
2. eset: Ha a+b>1, akkor létezik olyan c>1 valós szám, melyre T(n)=nc-vel definiált sorozat esetén T teljesíti a feltételt, továbbá T nyilván nem lineáris (mert c>1). c egyébként az a szám, melyre, ha a,b<1, akkor ac+bc=1 teljesül, ha a 1 vagy b 1 vagy b 1, akkor tetszőleges c>1 jó. 1, akkor tetszőleges c>1 jó.
3. eset Ha a+b=1, ekkor nem tudom mi van.
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|




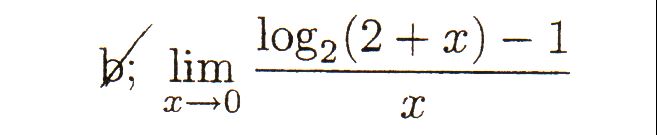

 /2-ben és ott folytonossá tehető.
/2-ben és ott folytonossá tehető.
 ), abból pedig az égéshő segítségével az összes munkát. A hasznos teljesítmény az összes munka szorozva a hatásfokkal. És ekkor már majdnem készen is vagy...
), abból pedig az égéshő segítségével az összes munkát. A hasznos teljesítmény az összes munka szorozva a hatásfokkal. És ekkor már majdnem készen is vagy... 

 3x ahol x
3x ahol x

 d*n minden n<N0-ra. Legyen most
d*n minden n<N0-ra. Legyen most