|
| [753] Valezius | 2009-01-21 20:22:43 |
 Láttam valamelyik topikban egy feladatot, de most az istenért se találom, valaki nem tudja, melyikben van?
ABCD konvex négyszög, ABD és ACD derékszög. Ugyanezekbe, mint háromszögbe írt körök középpontjai gyök(2) távolságra vannak.
Csak érdekelne, hogy jól emlékszem-e rá.
|
|
|
|
| [750] Gyöngyő | 2009-01-17 16:31:28 |
 Sziasztok!
Köszike Nadorp! Eszembe nem jutott,hogy sorbafejtesem.Nagyot koppant amikor elolvastam! Köszike még1szer!
|
|
|
| [748] nadorp | 2009-01-16 23:03:09 |
 Mivel nem volt logaritmus alap, ezért ez "hagyomány" szerint valóban ln-t jelent. Különben a 10-es alapú logaritmus lg. Az integrál kijön komplex integrállal is, ha az első negyedben levő egységnyi sugarú negyedkör ív és a két tengely által meghatározott zárt göbén integrálunk és a valós részeket nézzük, csak ez macerásabb számolás.
|
| Előzmény: [746] HoA, 2009-01-16 20:00:28 |
|
|
|
|
| [744] Gyöngyő | 2009-01-16 11:10:47 |
 Sziasztok!
Tud vki vmilyen ötletet adni a következő feladathoz: 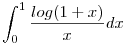
Thx: Gyöngyő
|
|
|
| [741] Valezius | 2009-01-11 17:24:46 |
 a kotangenst még én is ki tudom integrálni :) mert ugye az cos/sin, tehát az 1/sin épp a belső függyvény deriváltjával van szorozva. Azaz a másik tag: ln abs(sin x)
|
|
| [740] And | 2009-01-11 16:33:09 |
 Sziasztok! Ezt szeretném eintegrálni:
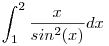
Próbáltam partiálisan integrálni: 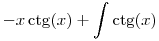
És ez lenne a végerendmény? tehát lehet tovább integrálni?
|
|
|
| [743] Suhanc | 2009-01-11 14:05:17 |
 Kedves And!
Ha szabad egy felvetéssel, javaslattal élnem: a fórumon már több olyan topic nyílt, melyben témafüggetlen, aktuális kérdések, problémák felvetése és megválaszolása folyik, példának hoznám a "Valaki mondja meg" és "Metematika segítségre van szükségem" topicokat. Önmagában már ez is "dőzsölés", hiszen úgy látom, a két topic teljesen azonos szerepet tölt be. Ezzel párhuzamosan többen nyitottak már új topicot egyetlen kérdés kedvéért; nem vagyok gyakori látogatója a fórumnak, de úgy látom, ezek a kezdeményezések 5-10 hozzászólást érnek meg, így vélhetően az előbb felsoroltak valamelyikébe is "beágyazhatóak". Javasolnám tehát, hogy "aktuális kérdéseinket" a fenti formában tegyük közlésre, elkerülve ezzel a kérészéltű topicok felhalmozását.
Üdvözlettel: Suhanc
* * *
A két témát összevontam. Moderátor
|
| Előzmény: [734] And, 2009-01-10 19:27:40 |
|
| [738] álmodozó | 2009-01-11 11:31:54 |
 Vegyük, észre, hogy
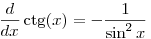
Vagyis az integrál:
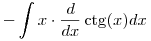
Csinálj egy parciális integrálást és kész
|
|
| [737] jonas | 2009-01-11 10:55:20 |
 Vizsgán, ha írásbeli, talán jobb, ha be is bizonyítod úgy, hogy egy lineáris helyettesítéssel megfordítod az integrált.
Az újabb integrál nagyon érdekes. Én ugyanis arra tippeltem volna, hogy az x/sin x-hez hasonlóan nem lehet zárt alakban felírni a határozatlan integrálját, de kiderül (táblázatból), hogy lehet. Nem tudom, hogy lehet levezetni, integrálásban nem vagyok jó.
|
| Előzmény: [736] And, 2009-01-10 22:52:55 |
|
| [736] And | 2009-01-10 22:52:55 |
 Sejtettem ,hogy ezt valahogy így meg lehet állapítani. Csak nem vagyok benne biztos ,hogy vizsgán elfogadják-e. Valamint még a következővel is bajba vagyok:
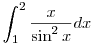
Nem tudom ,hogy a számlálóból az x-et hogyan kellene eltüntetni.
|
| Előzmény: [735] Lóczi Lajos, 2009-01-10 19:51:20 |
|
| [735] Lóczi Lajos | 2009-01-10 19:51:20 |
 Páratlan folytonos függvény origóra szimmetrikus intervallumon vett integrálja mindig nulla: a pozitív és negatív területek a szimmetria miatt kiejtik egymást.
|
| Előzmény: [734] And, 2009-01-10 19:27:40 |
|
| [734] And | 2009-01-10 19:27:40 |
 Valaki tudna segíteni ennek az integrálnak a levezetésében? Tudom ,hogy a végeredmény 0, de sehogyse jön ki.
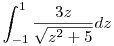
|
|
| [732] Gyöngyő | 2009-01-03 13:40:40 |
 Sziasztok!
segitséget szeretnék kérné,hogy hol találom meg az alábbi három tétel teljes bizonyitását:
Feltételes szélsőérték szükséges feltétele Darboux tétele arról,hogy az integrál határérték Potenciálfüggvény létezésének elegendő feltétele
Köszönöm előre is
Gyöngyő
|
|
|
| [730] epsilon | 2008-12-31 10:15:03 |
 BÚÉK Mindenkinek! Az a kérdésem lenne, hogy Valaki tud-e minél egyszerűbb megoldást a következő állításra? Előre is köszönöm, üdv: epsilon
|
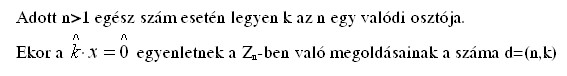 |
|
|