Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Fórum: Valaki mondja meg!

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]    [79]    [80]    [81]    [82]    [83]    [84]    [85]    [86]    [87]    [88]    [89]    [90]    [91]    [92]    [93]  

Szeretnél hozzászólni? Jelentkezz be.
[982] pdm2009-09-15 02:51:10

I(x+a,y+b)= I(x,y) + \frac {dI(x,y)} {dx}a + \frac {dI(x,y)} {dy}b

Hogy lehet az "a"-t és a "b"-t meghatározni?

Kösz.

[981] Lóczi Lajos2009-07-26 20:37:14

Megnézve a netes forrásokat Gauss munkájáról, ilyen utalásokat nem találtam: az algebra alaptételét a "közönséges" alakban mondja ki.

Előzmény: [980] Maga Péter, 2009-07-26 10:50:20
[980] Maga Péter2009-07-26 10:50:20

Én azt tippelem, hogy "rational integer"="racionális egész" (ezt szokták használni, amikor más számgyűrűk is játszanak, például Euler- vagy Gauss-egészek). Ilyenformán "rational integral algebraic function"="racionális egész együtthatós polinom"

Előzmény: [976] Zibin, 2009-07-23 21:25:00
[979] Tibixe2009-07-26 00:06:17

Szerintem valahogy így érti:

Minden racionális együtthatós polinom felbomlik első- és/vagy másodfokú valós együtthatós polinomok szorzatára.

Ez egy kicsit gyengébb állítás, mint az algebra alaptétele, de hihetőnek látszik, hogy csak ezt bizonyította.

[978] Zibin2009-07-24 08:53:40

Igazából az algebra alaptételének ezt az alternatív megfogalmazását ismertem, csak nem tudom... nem voltam benne biztos, hogy itt is erre gondol, mert valós polinomra nem hallottam még ezt a kifejezést. Mindenesetre köszönöm.

Előzmény: [977] Lóczi Lajos, 2009-07-23 23:09:02
[977] Lóczi Lajos2009-07-23 23:09:02

Akkor viszont ez a régies elnevezés a "valós együtthatós polinomra".

Előzmény: [976] Zibin, 2009-07-23 21:25:00
[976] Zibin2009-07-23 21:25:00

Gauss 1799-es doktori disszertációjának a címéből van, amelyben az algebra alaptételére adott bizonyítást, a címe angolul: "A new proof of the theorem that every rational integral algebraic function in one variable can be resolved into real factors of first or second degree"

A többi részét értem szerintem...

A segítséget előre is köszönöm

Előzmény: [975] Lóczi Lajos, 2009-07-23 20:12:27
[975] Lóczi Lajos2009-07-23 20:12:27

Én arra tippelek, hogy vmilyen racionális törtfüggvény, vagyis két polinom hányadosa, és esetleg a polinomok együtthatójára van vmi megkötés (pl. egész együtthatósak?). (Írj egy kicsivel több kontextust.)

Előzmény: [974] Zibin, 2009-07-23 14:15:29
[974] Zibin2009-07-23 14:15:29

Üdv! Szeretnék egy kis segítséget kérni: cikk olvasása közben találkoztam ezzel a kifejezéssel: "rational integral algebraic function"

Külön-külön a szavak jelentését tudom, és bár meglehet, hogy én vagyok csak túl analfabéta, de az egésznek nem tudom mi lehet a magyar megfelelője. Ha valaki tudná és megmondaná azt megköszönném.

[973] Tibixe2009-07-20 21:05:50

Az most nem segít.

[972] Koli142009-07-16 22:26:21

Tudom az m1-kamera illetve az m2-kamera távolságot pontosan. 1méter, 1,méter...

[971] Tibixe2009-07-16 17:22:09

Ha jól értem, hogy csak az M1-HF és M2-HF szakaszok hosszának arányát tudod, akkor abból még nem számolható semmi, mert ezekből az adatok még nem határozzák meg egyértelműen a hangforrás helyét.

A hangforrás egy bizonyos körön ( Apollóniusz-körön ) bárhol lehet.

Előzmény: [970] Koli14, 2009-07-16 16:52:47
[970] Koli142009-07-16 16:52:47

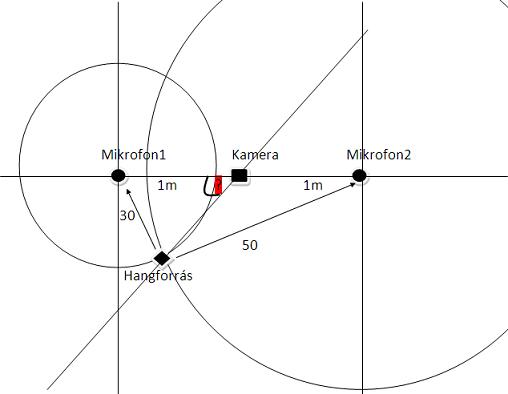
Sziasztok! Hogy tudom kiszámolni a piros kérdőjellel jelölt szöget? A helyzet az, hogy van 2 mikrofonom, illetve egy kamerám. A két mikrofonnal kiszámolom mondjuk egy tapsnak (ami a hangforrásból jön) az energáját. Ebből kapok 2 arányszámot. (ez az ábrán 30 és 50). A kamera és a mikrofonok távolságát tudom... Bárkinek valami ötlet? Köszi!

[969] Lóczi Lajos2009-07-15 15:17:07

Persze, hogy nem. (Nagyon kevés olyan sortípus van, amelynek az összege meghatározható. A többi szerencse kérdése.)

Előzmény: [968] vogel, 2009-07-15 10:52:09
[968] vogel2009-07-15 10:52:09

... egy konvergens sor összegének meghatározására?

Előzmény: [967] vogel, 2009-07-15 10:35:45
[967] vogel2009-07-15 10:35:45

Ebben az az érdekes (számomra), hogy "alkalmas" függvény Taylor-sorából. Általános módszer nem is létezik?

Előzmény: [966] Lóczi Lajos, 2009-07-14 15:25:01
[966] Lóczi Lajos2009-07-14 15:25:01

A legegyszerűbbeket alkalmas függvény Taylor-sorfejtéséből (pl. http://mathworld.wolfram.com/MaclaurinSeries.html). A többi után érdemes a szerzők nevére rákeresve utánanézni.

Előzmény: [965] Higgs, 2009-07-13 21:46:11
[965] Higgs2009-07-13 21:46:11

Pl. azokat amik itt vannak: http://hu.wikipedia.org/wiki/Pi

[964] Lóczi Lajos2009-07-13 19:14:29

Konkrétan melyeket?

Előzmény: [963] Higgs, 2009-07-12 19:04:51
[963] Higgs2009-07-12 19:04:51

Üdv! Köszönöm a linket, hasznos volt, és felvetett egy új kérdést. A pi-vel egyenlő végtelen sorokat, hogyan lehet levezetni?

[962] vogel2009-07-06 14:49:50

Itt találsz rá választ.

Előzmény: [961] Higgs, 2009-07-06 13:57:02
[961] Higgs2009-07-06 13:57:02

Üdv! Először is köszönöm a segítséget, de egy új kérdés merült fel bennem. A következő sor végtelen összegét hogyan lehet kiszámítani? 1/1*1+1/2*2+1/3*3+...+1/n*n Az összege pi*pi/6, de nem tudom ez, hogy jön ki.

[960] Csimby2009-07-05 11:54:10

Szia!

Nézd meg ezt!

Előzmény: [958] Higgs, 2009-07-05 00:47:01
[959] R.R King2009-07-05 06:42:22

Üdv.

Azt hiszem, hogy az általad megadott összegre nem létezik egyszerű zárt képlet. Egyébként nagyságrendet lehet mondani: az összeg nagyságrendileg kb. ln(n)

Sőt van egy olyan tétel, mely szerint az összeged-ln(n) konvergens és az Euler-konstans a határértéke

Előzmény: [958] Higgs, 2009-07-05 00:47:01
[958] Higgs2009-07-05 00:47:01

Üdv! A következő dolog érdekel. Az 1per1+1per2+1per3+...1pern-nek mi az összege?(azért írtam így, mert máshogy nem fogadta el.)

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]    [79]    [80]    [81]    [82]    [83]    [84]    [85]    [86]    [87]    [88]    [89]    [90]    [91]    [92]    [93]