KöMaL Problems in Physics, April 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 10, 2019. |
M. 386. Make a long-period torsion pendulum, which swings in air. With measurement determine how the period of the pendulum depends on the length of the thread.
(6 pont)
 |
Problems with sign 'G'Deadline expired on May 10, 2019. |
G. 669. Signs similar to the one shown in the figure can often be seen on highways to warn drivers to maintain a safe following distance. How can the following distance be given in seconds? Why is it that the appropriate ``following distance'' is two or more seconds?
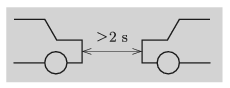
(3 pont)
solution (in Hungarian), statistics
G. 670. Different amount of samples of water of different temperature values are mixed. The corresponding volume and temperature data are the following: 1 litre water at \(\displaystyle 10\;{}^\circ\)C, 2 litres water at \(\displaystyle 20\;{}^\circ\)C, 3 litres water at \(\displaystyle 30\;{}^\circ\)C, 4 litres water at \(\displaystyle 40\;{}^\circ\)C, 5 litres water at \(\displaystyle 50\;{}^\circ\)C, 6 litres water at \(\displaystyle 60\;{}^\circ\)C, 7 litres water at \(\displaystyle 70\;{}^\circ\)C, 8 litres water at \(\displaystyle 80\;{}^\circ\)C and 9 litres water at \(\displaystyle 90\;{}^\circ\)C. What is the common temperature of the mixture if heat losses are negligible?
(3 pont)
solution (in Hungarian), statistics
G. 671. Two large, vertical and parallel plane mirrors are facing opposite to each other at a distance of 1 m. If you stand exactly midway between the mirrors outstretching your hand sideways, and observe the image of your palm reflected in one of the mirrors, you see quite a lot of images. What are the distances between the images of your palm?
(3 pont)
solution (in Hungarian), statistics
G. 672. A room has three doors, and next to each door there is a switch. With each of them the chandelier in the room can be switched on or off separately. In order to build such a circuit, multiway switches, namely 3-way and 4-way switches should be used. How can this circuit be built? Look up in literature how these switches work, and give the diagram of their connections.
(4 pont)
 |
Problems with sign 'P'Deadline expired on May 10, 2019. |
P. 5122. The braking distance of a car moving along dry and horizontal, asphalt-covered road at a speed of 50 km/h is at least 13 m, that is, the distance the car covers from the instant when the brakes are applied to when it comes to a complete stop. (In the definition of the braking distance the reaction time of neither the driver nor the vehicle are included.)

What is the minimum braking distance of the same car at a speed of 20 km/h on an unusually steep slope of angle of elevation of \(\displaystyle 30^\circ\) (approximately 58% slope)? Investigate both the upward and downward motions.
(4 pont)
solution (in Hungarian), statistics
P. 5123. There is a small object of mass \(\displaystyle m=0{.}25~\)kg at the left end of a trolley of mass \(\displaystyle M=1~\)kg and of length \(\displaystyle L=0.3~\)m. The trolley has vertical walls at its sides, and moves frictionlessly along the horizontal plane. Its small wheels are of negligible mass and size.
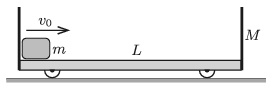
At a given instant the small object of mass \(\displaystyle m\) is given an initial speed of \(\displaystyle v_0=1~\)m/s towards the right. The coefficient of friction between the trolley and the object is \(\displaystyle \mu=0.1\). The collision between the object and the trolley can be considered elastic.
\(\displaystyle a)\) What is the speed of the trolley, when the object of mass \(\displaystyle m\) on it does not move with respect to the trolley?
\(\displaystyle b)\) How far is the object of mass \(\displaystyle m\) from the left wall of the trolley in the above asked case?
\(\displaystyle c)\) What are the velocities of the objects right after the moment of the first collision?
(5 pont)
solution (in Hungarian), statistics
P. 5124. \(\displaystyle a)\) Two alike solid cylinders are placed to the level tabletop next to each other and then carefully a third similar cylinder is placed to the top of the other two. What are the least values of the coefficient of static friction between the cylinders and between a cylinder and the table so that the arrangement stays at rest?
\(\displaystyle b)\) Three alike solid spheres are placed to the level tabletop next to each other and then carefully a fourth similar sphere is placed to the top of the other three. What are the least values of the coefficient of static friction between the spheres and between a sphere and the table so that the arrangement stays at rest?

(5 pont)
solution (in Hungarian), statistics
P. 5125. A slope of angle of elevation of \(\displaystyle \alpha =30^\circ\) is followed by a cylindrical surface of radius \(\displaystyle R=32~\)cm as shown in the figure. The cross section of the cylinder is three-quarters of a circular path started at the lowermost point of the circle \(\displaystyle T\), and the tangent to the circle at point \(\displaystyle T\) is in the plane of the slope. A uniform solid disc of mass \(\displaystyle m\) and of radius \(\displaystyle r\) is released without any initial speed from the plane. (Static friction is big enough everywhere, so the disc rolls down the slope without sliding. Rolling friction is negligible. The cylindrical surface is ideally smooth.)
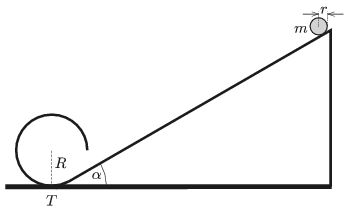
\(\displaystyle a)\) What is the radius of the disc if it just passes the gap below the cylinder?
\(\displaystyle b)\) What is the least height, measured from the ground, from which the disc should be released in order that it arrive back to the slope at a vertical velocity?
\(\displaystyle c)\) In this case what is the speed of the disc when it reaches the slope?
(5 pont)
solution (in Hungarian), statistics
P. 5126. The inside part of a circular-base vertical tube of height 1 m and of inner diameter 20 cm is filled with ice of temperature \(\displaystyle 0\;{}^\circ\)C. The wall of the tube is slippery and is made of some insulating material. The tube is open at its top and closed at its bottom. We start heating the bottom of the tube at a rate of 335 W.
At what constant speed will the top of the ice-cylinder move downwards?
(4 pont)
solution (in Hungarian), statistics
P. 5127. The total mass of a hot-air balloon (envelope + basket + load) is 320 kg. Initially the pressure inside and outside the envelope is \(\displaystyle 1.01\cdot10^5~\)Pa and its density is \(\displaystyle 1.29~\rm kg/m^3\). In order to raise the hot-air balloon a gas burner is used to heat the air inside the balloon. The volume of the envelope filled with hot air is 650 \(\displaystyle \rm m^3\), and the pressure inside does not change.
To what temperature must the air inside the balloon be heated in order that the balloon begin to rise?
(4 pont)
solution (in Hungarian), statistics
P. 5128. Two point-like charges of charge values \(\displaystyle Q\) and \(\displaystyle -3Q\) are at a distance of \(\displaystyle d\) in vacuum. Determine the electric flux through a disk of radius \(\displaystyle r=d/2\) at a distance of \(\displaystyle d_1=d/3\) from charge \(\displaystyle Q\). The centre of the disk is on the line segment which joins the two charges and the plane of the disk is perpendicular to the line segment.
(5 pont)
solution (in Hungarian), statistics
P. 5129. There is a circular conducting loop of radius \(\displaystyle R\ll \ell\) around a very long solenoid of radius \(\displaystyle r\), with number of turns \(\displaystyle N\) and of turn density \(\displaystyle n=N/\ell\), as shown in the figure. What is the reading on an ideal voltmeter connected across the terminals of the solenoid, if the current that flows in the circular loop is changing uniformly in time, according to the formula \(\displaystyle I(t)=\alpha\cdot t\)?
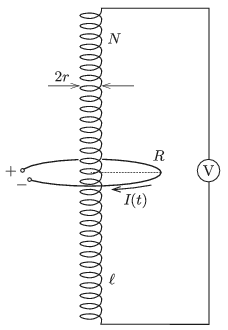
(5 pont)
solution (in Hungarian), statistics
P. 5130. The detected wavelength of the radiation coming from a star in a distant galaxy, and belonging to the electron transition of \(\displaystyle \rm 4d\to\rm 2p\) of the hydrogen atom is 513 nm. How far is the galaxy from us in light years?
(5 pont)
solution (in Hungarian), statistics
P. 5131. Three objects have the same, constant thermal heat capacities. Two of them have a temperature of 300 K, whilst the third one has a temperature of 100 K. Is it possible to heat one of them to a temperature of 400 K only by operating heat engines or heat pumps between the objects, so without adding external heat or performing external work?
(6 pont)
Upload your solutions above.
