KöMaL Problems in Physics, January 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 12, 2018. |
M. 374. Measure the refractive index of some type of honey.
(6 pont)
 |
Problems with sign 'G'Deadline expired on February 12, 2018. |
G. 621. The pressure of air at a height of 1 km is 899 hPa and its temperature is \(\displaystyle 8.6~{}^\circ\)C. At a height of 10 km the pressure is only 265 hPa, and the temperature is \(\displaystyle -37.2~{}^\circ\)C.
\(\displaystyle a)\) By what factor is the density of air smaller at the height of 10 km than that of at the height of 1 km?
\(\displaystyle b)\) By what factor is acceleration due to gravity smaller at the height of 10 km than that of at the height of 1 km?
(3 pont)
solution (in Hungarian), statistics
G. 622. A spherical gas container gets so warm in a hot summer day from morning to noon, such that its volume at noon differs by 0.6% from its volume in the morning. By what percent did the surface area of the container change?
(3 pont)
solution (in Hungarian), statistics
G. 623. A bucket of mass 10 kg is raised by means of a negligible-mass rope, such that first it is accelerated uniformly in 2 s to a speed of 0.6 m/s, and then it continues its motion at this speed for 8 more seconds. To what height is the bucket raised, and how much work was done?
(3 pont)
solution (in Hungarian), statistics
G. 624. Some of the newly established sailing boat ports at lake Balaton are ice-free, which means that even in very cold weather the water around the sailing boats do not freeze. This is due to the constant stirring of water. Why does this method work?
(3 pont)
 |
Problems with sign 'P'Deadline expired on February 12, 2018. |
P. 4991. Two objects of total mass 4 kg, one of them is hanging below the other and attached to it by means of a thread, are attached to the lower end of a spring, hung onto a stand, as shown in the figure. If the lower object falls down the other one at the end of the spring begins to oscillate. If the two objects are interchanged and the lower one falls the other also begins to oscillate. The difference between the periods is 0.3 s. Calculate the mass of each object if the period of the oscillatory motion when both objects are on the spring is 1.5 s.
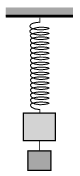
(4 pont)
solution (in Hungarian), statistics
P. 4992. A ball which was dropped from a height of \(\displaystyle h\) in a stationary elevator is bouncing for a time of \(\displaystyle t\).
\(\displaystyle a)\) What is the coefficient of restitution \(\displaystyle k\), which characterises the elasticity of the impact? (The constant \(\displaystyle k\) is the ratio of the linear momentum of the ball before the impact to that of after the impact.)
\(\displaystyle b)\) The elevator is moving upwards at a speed of \(\displaystyle v\). How long does the ball bounce when it is dropped from a height of \(\displaystyle h\)?
(5 pont)
solution (in Hungarian), statistics
P. 4993. The Channel Tunnel, between Calais and Dover has a length of 55 km, and 38 km of it is below the English Channel. Think of a 40 km long straight train tunnel on the exactly spherical Earth of radius 6371 km, below sea level, such that above the two ends of the tunnel the height of water is 20 m.
\(\displaystyle a)\) What is the height of water above the middle of the tunnel?
\(\displaystyle b)\) If there was no air in the tunnel and friction was also negligible, how long would it take for a train, starting from rest, to go through the channel due to just the gravitational pull of the Earth?
\(\displaystyle c)\) At what speed would the train go through the middle of the tunnel?
(5 pont)
solution (in Hungarian), statistics
P. 4994. The masses of both the wedge and the solid cylinder shown in the figure are \(\displaystyle m\), the radius of the cylinder is \(\displaystyle R\). The wedge can slide without friction on the ground. What is the minimum value of the coefficient of static friction between the wedge and the cylinder, if the cylinder rolls without slipping along the wedge and the angle of elevation of the wedge is \(\displaystyle \alpha=30^\circ\)?
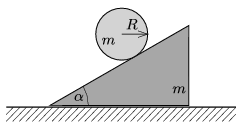
(5 pont)
solution (in Hungarian), statistics
P. 4995. Estimate the displacement of the centre of the mass of the Sun, due to the planets orbiting around it.
(4 pont)
solution (in Hungarian), statistics
P. 4996. In the process of \(\displaystyle p=\frac{\alpha}{V^2}\) (where \(\displaystyle \alpha\) is a constant) the volume of one mole helium was doubled, whilst its internal energy was decreased by 2493 J.
\(\displaystyle a)\) What was the initial temperature of the helium?
\(\displaystyle b)\) How much heat was released by the gas during the process?
(5 pont)
solution (in Hungarian), statistics
P. 4997. A point-like bead of mass \(\displaystyle m\), and of charge \(\displaystyle q\) can move frictionlessly along a horizontal semicircular path of radius \(\displaystyle R\). At each end of the semicircle there is a point-like fixed object of charge \(\displaystyle Q\). The system described is in equilibrium. What is the period of the motion of the bead if it is displaced a bit from its equilibrium position and then released?
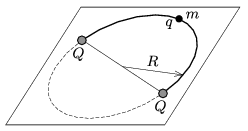
(5 pont)
solution (in Hungarian), statistics
P. 4998. A ray of light enters into a spherical water droplet, and after three total internal reflections it travels into its original direction as shown in the figure. What was the angle of incidence of the ray when it entered into the droplet? (The refractive index of water is \(\displaystyle n=4/3\).)
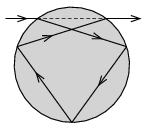
(5 pont)
solution (in Hungarian), statistics
P. 4999. In the device called JET (Joint European Torus, is the greatest ``tokamak'' type device in the world (http://www.euro-fusion.org/jet, in which the heating, the properties and the confinement of hot plasma, needed for the production of controlled nuclear fusion power, is investigated) deuterium (\(\displaystyle {}^2\)H) and tritium (\(\displaystyle {}^3\)H) nuclides fuse and create an \(\displaystyle \alpha\)-particle, and a neutron, while 17.62 MeV energy is liberated in each individual fusion.
\(\displaystyle a)\) The total liberated fusion energy by the Jet, when it produced the most power during an experiment, was 16 MW. How many grams of tritium and deuterium were used in the device in one second?
\(\displaystyle b)\) A fusion power plant is expected to produce electrical power of 1 GW. Suppose that the efficiency to transform the liberated nuclear energy to electrical energy is 35%. How many kilograms of deuterium and tritium would be used by this type of plant in one year?
\(\displaystyle c)\) Suppose that research on fusion power plants is successful, and by the year of 2050 the total electrical energy demand of all the 10 thousand million people (7000 kWh per person per year) living at that time on the Earth is supplied by fusion power plants. How many kilogram helium is generated in one year, and by what volume percent does the helium content of the atmosphere is increased? (Consider the atmosphere as a 5 km thick gas layer at standard conditions.)
(4 pont)
solution (in Hungarian), statistics
P. 5000. The U-shaped tube shown in the figure was filled with water. How, and by what amount will the level of the water in the arms of the tube change, if a current of \(\displaystyle I\) is made flow through the coil, of length \(\displaystyle \ell\) and of number of turns \(\displaystyle N\), tightly wrapped around the arm at the left-hand side? The diameter of the tube is much smaller than the length of the coil. (The relative permeability of water is \(\displaystyle \mu_{\rm r}\), its numerical value is just a very little bit less than 1.)
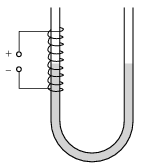
(6 pont)
Upload your solutions above.
