|
| [207] Sabroso | 2006-04-20 21:46:43 |
 Bocsi, de azt a 'szakadásmentes'-t kifejtenéd? Nekem ugyanis hiperbola jött ki koordinátageometriával.
Persze érdekes kérdés, hogy a 30o-os szöget bezáró érintők az érintőszakaszokat vagy az egyeneseket jelentik. Ha az előbbi, akkor csak a hiperbola alsó ága lesz megfelelő, szerintem ezt találhattad meg.
|
| Előzmény: [206] Iván88, 2006-04-20 21:42:58 |
|
| [206] Iván88 | 2006-04-20 21:42:58 |
 Sziasztok. Elakadtam a B.3901-essel (Az a parabolás)
Odáig jutottam, (sajnos ábrát nem tudok feltölteni) hogy (A parabola fókusza F, vezéregyenese v,) Az összes ilyen P pontra igaz, hogy a P középpontú PF sugarú körök metszéspontjait v-vel E1-gyel és E2-vel jelölve a PE1E2 háromszög szabályos. (Kiss György tavalyi kúpszeletes cikkében van néhány hasznos infó, de nem elég...)
A keresett alakzat nyilvánvalóan szimmetrikus az F-ből v-re bocsájtott merőleges egyenesre, biztosan szakadásmentes és nyítl.
Euklidesszel megnéztem, és 99,9999 százalék, hogy a keresett alakzat szintén parabola, de itt akadtam el.
Valaki aki tud segítsen. (Koordináta-renszerbe betéve semeddig sem tudtam eljutni, szerintem túl sok jó megoldás nem lesz :o) )
|
|
| [205] rizsesz | 2006-04-20 15:52:35 |
 mármint az én időmben, azaz 2002-ben :)
|
|
| [204] rizsesz | 2006-04-20 15:52:15 |
 emellett még a 11. osztályos matek oktv 2. és döntő fordulójából is volt példa...
|
|
| [203] Sümegi Károly | 2006-04-20 15:50:37 |
 Idén eddig legalább 10-15 olyan feladat volt B-ben, ami könyvekben megtalálható. Ezt nem tartom kifejezetten szerencsésnek. Ezt a feladatot én nem találtam meg, de ki tudja mennyi feladatot tűztek ki még máshol.
|
| Előzmény: [202] rizsesz, 2006-04-20 00:57:37 |
|
| [202] rizsesz | 2006-04-20 00:57:37 |
 A B.3875.-höz kapcsolódóan a 2002. májusi szám egyik feladata:
B.3555. Egy 2n+1-tagú társaság bármely n-tagú csoportjához van a társaságnak olyan a csoporthoz nem tartozó tagja, aki a csoport minden tagját ismeri. Az ismeretséget kölcsönösnek tételezzük fel. Bizonyítsuk be, hogy a társaságnak van olyan tagja, aki mindenkit ismer. (5 pont) ...
|
|
| [201] Iván88 | 2006-04-06 15:13:30 |
 Kösz!
Az igazat megvallva nekem volt hozzá könyvem, onnan néztem ki, de ez nem tilos.
De azért ez az 5 pontosok között is egy nehezebb feladat volt.
Én hamar eljutottam odáig, hogy
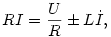
innentől a diff. egy. az kézenfekvő, csak nem tananyag...
|
| Előzmény: [200] CsG, 2006-04-05 22:58:59 |
|
| [200] CsG | 2006-04-05 22:58:59 |
 Igen, diff. egyenlet nélkül is megoldható. Ha felhasználod, hogy a fluxus egyenesen arányos az áramerősséggel, és hogy a fluxus hirtelen nem változhat (tehát állandó). Ellentétes tekercselésnél a fluxusok kivonódnak egymásból, azonos menetiránynál pedig összeadódnak. Ezekből is ugyanúgy kijön, amire te is jutottál.
|
| Előzmény: [199] Iván88, 2006-04-05 20:19:34 |
|
| [199] Iván88 | 2006-04-05 20:19:34 |
 Már régen írtam megoldást!
A P.3872.-esre a megoldásom: (sajnos az ábrát nem bírta a rendszer feltölteni)
A kapcsolós ág a Kettes, a másik az 1-es. A Kettes ág nyitva van, tehát ott nyitás után semmikor sem folyhat áram. (feszültség persze indukálódik...)
Az 1-esben viszont:
a) Ha a tekercselés azonos, akkor a vasmagman-nyitás előtt-a mágneses indukció nagysága(jó közelítéssel) 0 .
Ha nyitjuk a Kapcsolót, akkor bekapcsolási jelenséget figyelhetünk meg. Azaz az indukált feszültség és a telep feszültsége egymást rontja. Mint ismeretes:
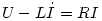
Ez I-re egy elsőfokú differenciálegyenlet, azaz
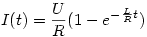
(Mivel I(0)= ) Tehát ) Tehát  . Így közvetlenül a nyitás után sehol sem folyik áram. . Így közvetlenül a nyitás után sehol sem folyik áram.
b) Itt viszont nyitás előtt a B-k egymást erősítik, azaz az egyes tekercsek mégneses indukciója (mely mindkét tekercsnél ugyanakkora) fele a vasmagban lévőnek. Nyitás után a B értéke a felére csökken, tehát egy kikapcsolási jelenség figyelhető meg nyitáskor, így az indukált feszültség( ), és a telep feszültsége egymást erősítik. Így: ), és a telep feszültsége egymást erősítik. Így:
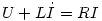
. Ennek a megoldása:
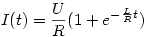
(I(0)=UR) Tehát

Tehát ez esetben az áramerősség értéke kezdetben a nyitás előttinek a duplája.
De vajon differenciál egyenletek nélkül ez megoldható?
|
|
|
|
| [196] Sabroso | 2006-04-05 17:05:03 |
 Bocs, de ezt nem értem. Ha x és y racionálisak, abból szerintem nem következik, hogy 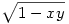 is racionális. is racionális.
Viszont az én megoldásom szerintem jó, csak eléggé kitalálhatatlan: Osszunk át x2y2-tel (x=y=0-ra nyilván igaz az állítás)
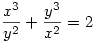
Jelöljük most  -et a-val! Ekkor -et a-val! Ekkor
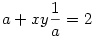
Ahonnan a-val fölszorozva
a2-2a=-xy
, tehát
(a-1)2=a2-2a+1=1-xy
Persze az egy jó kérdés, hogy miért nem szimmetrikus az a... Megpróbáltam végig levezetni, de egy kicsit hosszadalmas, úgyhogy inkább nem írnám le :)
|
| Előzmény: [195] jenei.attila, 2006-04-04 23:09:30 |
|
| [195] jenei.attila | 2006-04-04 23:09:30 |
 A B.3891 feladat megoldása. A feladat: x,y racionális számokra x5+y5=2x2y2. Biz. be, hogy 1-xy egy racionális szám négyzete.
Megoldás: Az egyszerűség kedvéért vezessük be a p=xy jelölést. Az egyenletből:
y5=2p2-x5
. Ezzel a helyettesítéssel írjuk fel p5-t.
p5=x5(2p2-x5)
, vagyis
x10-2p2x5+p5=0
x5-ben másodfokú egyenletet kapjuk. Ebből
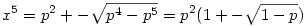
. Mivel x,y racionális 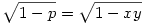 is racionális. is racionális.
|
|
| [194] Mate | 2006-03-24 17:07:19 |
 Igen, azt hiszem, jó ez a megoldás, bár nem számoltam utána. Majd a többivel együtt kijavítom ezt is. Én ilyen megoldást vártam, és Iván hozzászólása alapján nem is értem, hogy lehetett ezt másképpen értelmezni.
|
| Előzmény: [193] [evilcman], 2006-03-24 16:01:00 |
|
|
| [192] Iván88 | 2006-03-24 15:36:01 |
 P.3867. Egyenletes sűrűségű, állandó keresztmetszetű, nyújthatatlan, függőlegesen lógó szál valamilyen L hosszúságnál a saját súlya alatt leszakad. Elképzelhető-e olyan alakú szál, amely akármilyen hosszú lehet, mégsem szakad el a saját súlya alatt?
|
| Előzmény: [191] Mate, 2006-03-24 15:30:48 |
|
| [191] Mate | 2006-03-24 15:30:48 |
 Sziasztok!
A feladatot én tűztem ki, de mivel nekem már nem jár a KöMaL, nem tudom, pontosan hogyan szólt a feladat szövege. Az biztos, hogy én arra gondoltam, amit Onogur írt, hogy a szál keresztmetszetének nagysága változik a hossz függvényében. Hatványfüggvény nem lehet a szál alakja, hiszen ez esetben egy "végtelen" hosszú szál tömege is végtelen nagy. Valaki írja be pontosan a feladat szövegét!
|
|
| [190] Hajba Károly | 2006-03-24 13:52:41 |
 Egy kicsit pontosítanék a felírt képleten, hogy szakszerűbb legyen.
A szakítószilárdsági határ miatt 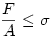
![k\int_x^\infty[f(x)]^2dx \le [f(x)]^2](keplet.cgi?k=8E08B22E2DBCD867)
ahol k egy az anyag sűrűségével és szakítószilárdságával ill. gravitációs gyorsulással arányos és 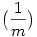 mértékegységű konstans. mértékegységű konstans.
|
| Előzmény: [189] Hajba Károly, 2006-03-24 12:43:54 |
|
| [189] Hajba Károly | 2006-03-24 12:43:54 |
 Üdv!
Szerintem a feladat második mondata nem utal az állandó keresztmetszetre, így valóban forgástestről is lehet szó. Elvileg ebben az esetben nem a (központosan szimetrikus) forma, hanem a keresztmetszeti felület nagysága érdekes, de számolni kör keresztmetszettel célszerű. Gyakorlatilag egy adott magasságban található keresztmetszet nagysága arányos az alatta található végtelen hosszú és egyre vékonyabb "rúd" térfogatával.
A következők csak tipp, mivel kb. 20 éve nem foglalkoztam ezzel. Tehát, ha jó az elképzelésem és jól írom fel a következő egyenletet, akkor ennek megoldása adja a rúd alakjának függvényét.
![\int_x^\infty[f(x)]^2dx = [f(x)]^2](keplet.cgi?k=DAE704663CF4325F)
De gondolom, majd Máté rendberakja a dolgokat. :o)
|
| Előzmény: [187] HoA, 2006-03-24 11:06:09 |
|
| [188] Iván88 | 2006-03-24 12:10:37 |
 Szia HoA!
Én úgy értelmeztem a feladatot, hogyha a keresztmetszete állandó, akkor valamekkora L-nél elszakad.
Szerintem olyan alakúnak kell lennie, hogy a tömege véges legyen, akármilyen hosszú is. Ha a keresztmetszete állandó, akkor nyilván nem beszélhetünk véges tömegről végtelen hosszúság mellett.
Így muszáj neki vékonyodnia.
|
| Előzmény: [187] HoA, 2006-03-24 11:06:09 |
|
| [187] HoA | 2006-03-24 11:06:09 |
 Lehet, hogy nem jól értem a feltételeket, de nekem az "Egyenletes sűrűségű, állandó keresztmetszetű, nyújthatatlan, függőlegesen lógó szál" azt jelenti, hogy egy hengerszerű testről van szó, melynek tömege és így súlya is egyenesen arányos az L hosszúsággal. Ez áll az állandó keresztmetszet miatt az egységnyi keresztmetszetre ható erőre is. Ha feltételezzük, hogy a szál szakítószilárdsága véges 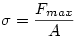 , kellően hosszú szál esetén biztosan elszakad. Csak az nem világos, hogy merül fel egyáltalán a keresztmetszet alakja. , kellően hosszú szál esetén biztosan elszakad. Csak az nem világos, hogy merül fel egyáltalán a keresztmetszet alakja.
|
| Előzmény: [186] Iván88, 2006-03-23 21:38:29 |
|
| [186] Iván88 | 2006-03-23 21:38:29 |
 Sziasztok!
A P.3867.-esre van valakinek megoldása?
Az én tippem az, hogy a szál alakja legfeljebb valamilyen 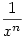 tengelymetszetű forgástest lehet, de ez sak tipp. tengelymetszetű forgástest lehet, de ez sak tipp.
|
|
|
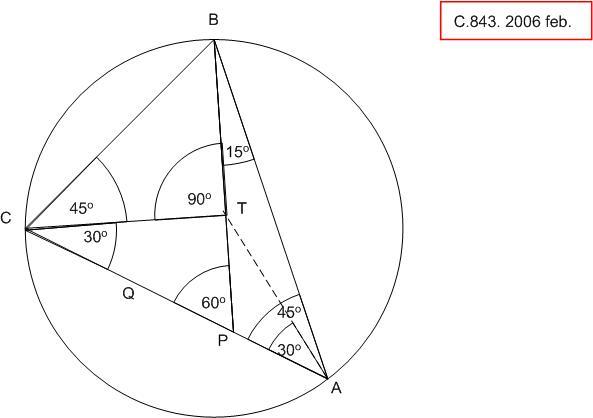
| [184] HoA | 2006-03-20 10:44:57 |
 C.842 helyett C.843
A megoldás természetesen jó, de kicsit "deus ex machina". Ugyanezeket az elemeket felhasználva egy konstruktív megoldás:
BPC  = 45 + 15 = 60o . Bocsássunk merőlegest C-ből BP-re, talppontja legyen T. Ekkor CPT 60o -os derékszögű = 45 + 15 = 60o . Bocsássunk merőlegest C-ből BP-re, talppontja legyen T. Ekkor CPT 60o -os derékszögű  , PT = PQ = PA . PAT egyenlőszárú , PT = PQ = PA . PAT egyenlőszárú  , TAP , TAP  = 30o , BAT = 30o , BAT  = 15o . TCA egyenlőszárú = 15o . TCA egyenlőszárú  ( két 30o -os szög ) TC = TA, TAB egyenlőszárú ( két 30o -os szög ) TC = TA, TAB egyenlőszárú  ( két 15o -os szög ) TB = TA . Így TC = TB, TBC derékszögű ( két 15o -os szög ) TB = TA . Így TC = TB, TBC derékszögű  egyenlőszárú, TCB egyenlőszárú, TCB  = 45o . (És persze kiderül, hogy T tkp. O ) = 45o . (És persze kiderül, hogy T tkp. O )
|
 |
| Előzmény: [179] Káli gúla, 2006-03-19 14:52:01 |
|







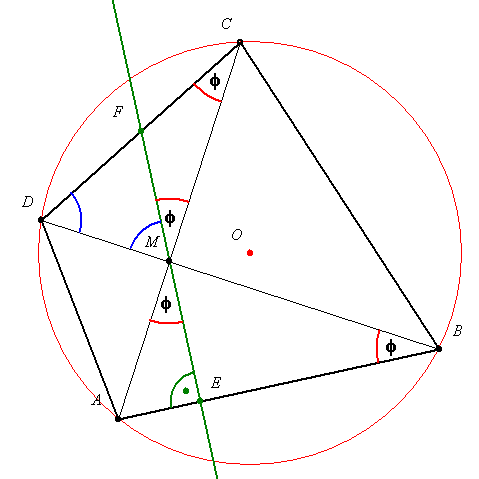
 =ACD
=ACD mert a DA iven nyugvó kerületi szögek. ABD
mert a DA iven nyugvó kerületi szögek. ABD egyenlő szárú és egyenlő szárú a DMF
egyenlő szárú és egyenlő szárú a DMF