Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[27] lorybetti

2003-12-15 21:26:01

Kedves Ákos!

Ugyanigy oldottam meg én is ezt a feladatot. Talán még szerencsésnek is mondhatom magam, mert 1 pontot kaptam, és szeretném tudni, miért!

Előzmény: [25] Gyarmati Ákos, 2003-12-15 21:14:14

[26] PálinkásCsaba	2003-12-15 21:22:45
Én már sokat gondolkoztam, hogy miért vontak le 1 pontot a B.3670-nél,talán azért mert nem igazoltam, hogy a 30,60,90 fokos háromszög hozzáírt körei valóban teljesítik is a feladat feltételeit így az általunk talált szöghármas elégséges is, nemcsak szükséges. De ez csak találgatás (nekem is 4 pont lett) kíváncsi vagyok az igazi helyes megoldásra.
Előzmény: [24] Csimby, 2003-12-12 18:38:49

[25] Gyarmati Ákos

2003-12-15 21:14:14

B. 3668-as feladatra én a következő megoldást adtam:

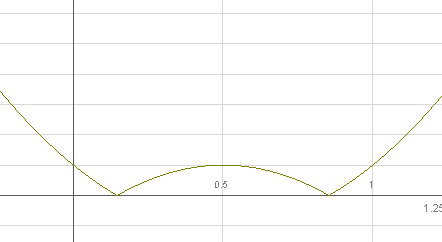
Alakítsuk át a függvényt f(x)=(x–u)²+v alakúra. Mivel a függvény képe egyenes állású parabola, ezért minimumértéke v lesz, ekkor x=u. Az abszolútérték, miatt a már transzformált függvény maximumértéke lesz. Mivel abs((x-u)²+v)<=1/8 , ezért abs(v)=1/8, v=-1/8 . Mivel a függvény képe a parabola tengelyesen szimmetrikus (tengelye x = u-ban van), ezért ahhoz, hogy a parabola mindkét ága a megadott értéken belül maradjon, a [0;1] intervallumon, tengelyének u=0,5-ben kell lennie. Ha u-t nagyobbra választanánk (u=0,5+p, p eleme R(+) és p < 0,5), akkor az 0 < x < p szakaszon a függvény értéke nagyobb lenne, mint . Hasonlóképpen látható, hogy ha u-kisebbre választanánk mint 0,5 (u=0,5–p, p eleme R(+) és p < 0,5) akkor az (1 – p) < x < 1 szakaszon nem teljesülne a feltétel. Tehát u=0,5. Ekkor a függvény, így néz ki: f(x)=(x–0,5)²–0,125. Az eredeti függvényt teljes négyzetté alakítva: x²–ax–b=(x-a/2)²-(a²)/4-b. Tehát a/2=0,5,a=1. Ekkor b=-1/8, f(x)=x²–x+1/8 .Tehát a=1, és b=-1/8.

Én a megoldást függvényként ábrázoltam, és abból is az derül ki, hogy a és b ezen értékei megfelelnek.

Ennek ellenére 0 pontot kaptam. Szeretném megtudni miért?

[24] Csimby	2003-12-12 18:38:49
A B.3670-es példában volt valami rejtett gonoszság, vagy csak egy keménykezű javítóhoz került? Ugyanis szinte senki sem kapott rá 5 pontot... Valaki mondja meg aki rájött, miért kapott/nem kapott max. pontot.

[23] Kós Géza

2003-12-11 10:03:40

Én inkább a b_n=x_n²+y_n²+z_n² összeggel írtam volna a megoldást, azzal majdnem szó szerint ugyanúgy jön ki, hogy

$b_{n+1}=x_{n+1}^2+y_{n+1}^2+z_{n+1}^2= \left(y_n+\frac1{z_n}\right)^2+ \left(z_n+\frac1{x_n}\right)^2+ \left(x_n+\frac1{y_n}\right)^2>$

$>x_n^2+y_n^2+z_n^2+ 2\left(\frac{y_n}{z_n}+\frac{z_n}{x_n}+\frac{x_n}{y_n}\right) \ge b_n+6\root3\of{\frac{y_n}{z_n}\cdot\frac{z_n}{x_n}\cdot\frac{x_n}{y_n}}=b_n+6,$

és b₂₀₀>b₁+199^.6>1200.

Előzmény: [22] Rácz Béla, 2003-12-10 18:48:01

[22] Rácz Béla	2003-12-10 18:48:01
Ha a B-feladatra gondolsz, a szeptemberiek megoldásai már a honlapon is fenn vannak, itt.
Előzmény: [21] Suhanc, 2003-12-09 21:38:02

[21] Suhanc	2003-12-09 21:38:02
A szeptemberi egyetlen 5 pontos feladat megoldását fel tudná valaki tenni?

[20] Suhanc

2003-12-07 13:46:49

Kedves Nadorp!

Most volt türelmem végigolvasni! Nagyon ravasz!!!

[19] nadorp

2003-11-27 15:56:44

B3671

Megpróbálok vázlatosan leírni egy megoldást. Nem túl szép, de jónak tűnik.

Előszőr is alakítsuk át a baloldalt:

(x²+y)(x+y²)=x³+y³+xy+x²y²=(x+y)[(x-y)²+xy]+xy(xy+1)=(x+y)(x-y)²+(x+y)xy+xy(xy+1),azaz

(x+y)(x-y)²+xy(x+1)(y+1)=(x-y)³

2y(x-y)²+xy(1+x)(1+y)=0

Innen y=0 és x bármely egész az egyik megoldás.

Ha y $\ne$ 0, akkor y-nal osztva és felhasználva, hogy (x-y)=(1+x)-(1+y)

2(1+x)²-4(1+x)(1+y)+2(1+y)²+x(1+x)(1+y)=0

2(1+x)²+(x-4)(1+x)(1+y)+2(1+y)²=0

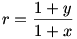Ha x=-1, akkor y=-1 és ez is megoldás. Ha x $\ne$ -1, akkor bevezetve az $r=\frac{1+y}{1+x}$ új változót, kapjuk

2r²+(x-4)r+2=0

Ez egy egész együtthatós másodfokú egyenlet, melynek racionális megoldását keressük. Ez csak úgy lehet, ha a diszkrimináns négyzetszám, azaz

(x-4)²-16=z² , ahol z egész.

Könnyen ellenőrizhető, hogy két négyzetszám különbsége csak két esetben lesz 16:

25-9=16 vagy 16-0=16. Innen

(x-4)²=25 vagy (x-4)²=16 adódik, azaz

x= 0 ,8 vagy 9 lehet. ( Az x=-1 esetet már kezeltük).

Innen már y könnyen meghatározható.Az összes megoldás:

x= bármely egész szám , y=0

x=-1 , y=-1

x=8 , y=-10

x=9 , y=-6

x=9 , y=-21

Előzmény: [3] Suhanc, 2003-11-20 14:40:16

[18] Kós Géza 2003-11-26 11:16:34

BTW Béla, mikor tanulsz meg legalább egy kicsit szépen írni? Egyáltalán nem kidobott idő. Ha nagy leszel, úgyis minden cikket TeX-ben kell majd írnod. (Ez még akkor is igaz, ha nem matematikus, hanem fizikus leszel :-P)

Az alsó és felső indexek írása meg semmiség, pl. $H_{i+2}^2$ = H_i+2². De az egész TeX minitanfolyamon is átrághatod magad egy óra alatt.

U.I. Rég láttalak a Tom és Jerryben.

[17] Kós Géza

2003-11-26 11:06:11

Én is erre tippeltem.

Ezeket az azonosságokat Newton-Girard formuláknak hívják (lásd pl. itt), de hallottam már a Newton-Waring-Girard formulák elnevezést is.

Előzmény: [14] Rácz Béla, 2003-11-25 21:00:07

[16] Rácz Béla

2003-11-25 22:51:00

Kösz, Peti!! Benned bíztam!

Szóval, kedves Géza! Irodalomként hivatkozom Pach Péter Pál alábbi hozzászólására!

[15] Pach Péter Pál

2003-11-25 22:41:52

Én úgy emlékszem, hogy Tihamér éppen a k $\ge$ n esethez tartozó összefüggést nevezte Newton-tételnek. Biztos, hogy „sokkal könnyebb bizonyítani”? Az igaz, hogy ott működik egy olyan bizonyítás is, ami sokkal rövidebb, de a 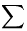$\sum$ -s felírás mindkettőt kihozza. Remélem mindenki kitalálja, hogyan működik a jelölés. :-)

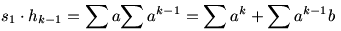
$s_1 \cdot h_{k-1} ={\sum a}{\sum {a^{k-1}}}={\sum {a^k}}+{\sum {a^{k-1}}b}$

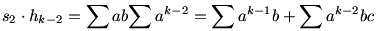
$s_2 \cdot h_{k-2} ={\sum ab}{\sum {a^{k-2}}}={\sum {a^{k-1}b}}+{\sum {a^{k-2}}bc}$

És így tovább…

Az ilyen típusú egyenleteket kell összeadni, hogy megkapjuk azt a tételt, amit (legalábbis ebben a témában) Newton-tételnek hívunk. A végén (az utolsó egyenletnél) egyébként éppen k $\le$ n miatt „jön be” a k-as szorzó.

Előzmény: [14] Rácz Béla, 2003-11-25 21:00:07

[14] Rácz Béla

2003-11-25 21:00:07

Hát biztos az a baj, hogy nem ez a neve ...

Szóval, az állítás a következő:

Ha van n szám, és bármely i-re H(i) a számok i. hatványösszege, S(i) pedig az összes i-szeres szorzat összege (ami a Vieta-formulákban szokott pl. felbukkanni), akkor k <= n esetén

H(k) = S(1)*H(k-1) - S(2)*H(K-2) + S(3)*H(K-3) - ... + (-1)i*S(i)*H(k-i) + ... + (-1)k*S(k-1)*H(1) - (-1)k*k*S(k)

Például (k=3-ra):

H(3) = S(1)*H(2) - S(2)*H(1) + 3S(3), ez tényleg nagyon ismert.

Nagyon hasonló állítás igaz akkor is, ha k >= n, csak azt sokkal könnyebb bizonyítani.

Olimpiai felkészülésen mint ismert tételre hivatkoztak erre; azt hiszem, ott hallottam rá azt a nevet, hogy Newton-tétel. Most akkor utánanézek.

Előzmény: [10] Kós Géza, 2003-11-24 16:35:36

[13] Csillag	2003-11-25 20:38:11
:)
Előzmény: [12] Kós Géza, 2003-11-24 19:27:19

[12] Kós Géza

2003-11-24 19:27:19

Blöffölni tudni kell. :-)

Tegnap hallottam, hogy valaki egy versenyen hivatkozott a "Csimkin féle fokszámeltolási tételre", és ezt még egy hivatkozással is megtoldotta egy orosz nyelvű lap 30 évvel ezelőtti számára. Elhitték neki.

Előzmény: [10] Kós Géza, 2003-11-24 16:35:36

[11] Csillag

2003-11-24 18:50:44

Szia Béla!

Ezt megkaptad!:)

Amúgy avass be, hogy hol olvastad a tételt!

Köszi mindannyiunk nevében!

Előzmény: [9] Rácz Béla, 2003-11-22 20:49:47

[10] Kós Géza

2003-11-24 16:35:36

Szia Béla,

Számomra nem egyértelmű, hogy mi az a ,,polinomos Newton-tétel'', de ha tisztességesen hivatkoztál rá, akkor nem lehet gond.

Előzmény: [9] Rácz Béla, 2003-11-22 20:49:47

[9] Rácz Béla

2003-11-22 20:49:47

Az A. 326. példáról szeretnék kérdezni. (Géza, figyelem!)

Szóval: baj, ha felhasználtam a polinomos Newton-tételt, mint nagyágyú?

[8] lorantfy

2003-11-22 16:48:22

Bocs! A vége rossz lett:

... amiből: (a+b+c)(a+b-c)=2ab

(a+b)²-c²=2ab, vagyis a²+b²=c²

Előzmény: [7] lorantfy, 2003-11-21 14:00:31

[7] lorantfy

2003-11-21 14:00:31

Kedves Rizsa!

Jól néz ki a megoldás, de én az alábbi két egyenlet összevetéséből:

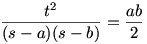
$\frac{t^2}{(s-a)(s-b)}=\frac{ab}{2}$

t²=s(s-a)(s-b)(s-c)

ezt kapom: 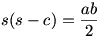$s(s-c)=\frac{ab}{2}$ , amiből (a+b+c)(a+b)=2ab

Elírtál valamit vagy csak én vagyok túl fáradt?

Előzmény: [6] Rizsa, 2003-11-21 11:39:25

[6] Rizsa

2003-11-21 11:39:25

en igy oldottam meg a b. 3671.t:

Ra = t/(s-a) Rb=t/(s-b), r=abc/4t

Ra+Rb= t*(1/(s-a)+1/(s-b))=t*c/((s-a)*(s-b))=2r=abc/2t, mert s-a+s-b=2s-(a+b)=c.

ebből t*t/((s-a)*(s-b))=ab/2. t*t=s*(s-a)*(s-b)*(s-c), egyszerusitve (s-a)*(s-b)=ab/2

s-a=(b+c-a)/2, s-b=(a+c-b)/2.

Ebből (b+c-a)*(a+c-b)=2ab.

c*c-(a-b)*(a-b)=2ab, amiből c*c=a*a+b*b, gamma=90fok. ugyanigy a masik szog 60 fok, tehat a harmadik szog 30fok. szerintem igy egyszerubb :)

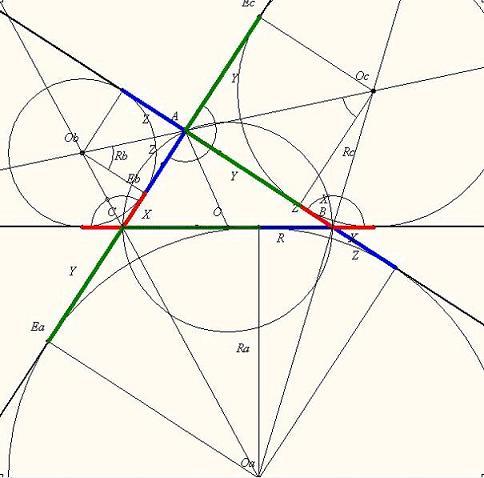
[5] lorantfy

2003-11-20 23:50:49

2. Ha $\alpha$ =90^o , akkor a hozzáírt körök középpontjai, az érintési pontok és az A csúcs négyzeteket alkotnak, igy

Ra=Z+X+Y,Rc=Y

Az Ra – Rc = R egyenletbe beírva Z + X = R.

Tehát a háromszögben AC = Z + X = R, és BC = 2 R miatt $\beta$ =30^o és $\gamma$ =60^o

[4] lorantfy

2003-11-20 23:34:00

B.3670. megoldása

I. Ra+Rb=3R, II. Rb+Rc=2R amiből:

III. Ra–Rc=R

1.Belátjuk, II-ből következik, hogy a háromszög derékszögű,.

2.Belátjuk, III-ből következik, hogy $\beta$ =30^o és $\gamma$ =60^o

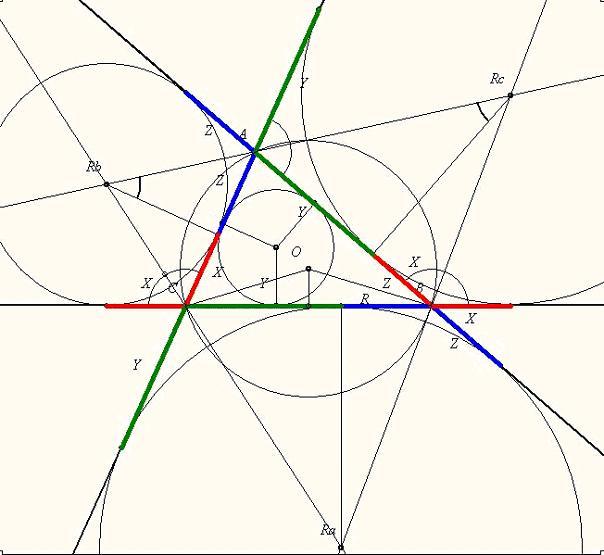
1. Az egyenlő érintőszakaszokat azonos betűkkel: X, Y, Z jelöljük. A BCO háromszögben

2Rsin $\alpha$ =Y+Z

Ez a két szakasz Rb és Rc sugarakkal is kifejezhető:

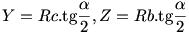
$Y = Rc. \tan\frac{\alpha}{2} , Z = Rb. \tan\frac{\alpha}{2}$

amiből

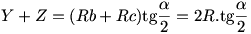
$Y + Z = ( Rb + Rc) \tan\frac{\alpha}{2} = 2 R. \tan\frac{\alpha}{2}$

Tehát 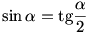$\sin\alpha =\tan\frac{\alpha}{2}$ és 0< $\alpha$ <180^o, amiből $\alpha$ =90^o : a háromszög derékszögű.

[3] Suhanc

2003-11-20 14:40:16

Üdvözlet mindenkinek! Leírom a rádiós feladatra a megoldásomat. Sajnos eléggé hosszúra sikerült: Ábrázoljuk az elemeket egy 8 csúcsú gráf pontjaival. Ha 2 csúcsot él köt össze, akkor azt a két elemet egy lépésben betettük a készülékbe. Ez alapján egy él /próbálkozás/ rossznak minősül, ha legalább egyik végpontja rossz csúcs (elem). Állítás: legalább 7 kísérletre van szükség. Először azt lássuk be, hogy 6 él esetén még nem biztos, hogy van köztük jó él. Indirekten bizonyítsunk, tfh:6 él minden esetben elég ahhoz, hogy legyen jó él! Válasszuk két részre a bizonyítást: 1. Van olyan csúcs a 8 közül,amelyből legalább 3 él indul. 2. Minden élből legfeljebb 2 él indul. 1. esetben tekintek egy olyan csúcsot, amelyből legalább 3 él indul. Legyen ez a csúcs (elem) rossz! Ekkor a hat csúcsból legalább három rossz! Ha a maradék (legfeljebb) 3 él 1-1 csúcsa rossz, úgy az összes él rossz. Ez lehetséges, mert 4 rossz elem van, és az előbb is legfeljebb 4 csúcsnak kellett rossznak lennie. Tehát ez esetben nincs biztosan jó él! 2. esetben legalább 4 olyan csúcsnak kell lennie, amelyből pontosan 2 él indul.Ellenkező esetben az élek számának maximuma (ha 3csúcsból 2, 5 csúcsból 1 él indul) 11/2 lenne, de nekünk 6 él kell. Tehát van 4 ilyen csúcs. Tekintek két olyan csúcsot, amelyből pontosan két él indul, és nem köti össze őket él. Ilyen biztosan van, mert 1 ilyen csúcsot legfeljebb 2 másik ilyen csúccsal köthetek össze, és legalább 3 másik van. Legyen a kiválasztott 2 csúcs rossz! Ekkor a hozzájuk tartozó 2-2 él rossz, tehát a 6 élből négy rossz. Ha a maradék 2 él 1-1 csúcsa rossz, akkor az összes él rossz. Ez lehetséges, mert négy rossz elem van, és most is legfeljebb 4 csúcsnak kellett rossznak lennie. Tehát ez esetben sem lesz biztosan jó él. Azaz 6 kísérlet kevés a biztos eredményhez! Most még azt kell belátni, hogy hét él esetén biztosan lesz jó él, ha megfelelően választjuk meg az éleket. Erre elégséges egy konstrukciót készíteni. Legyen a 8 csúcs A;B;...H, és legyenek AB; CD; CE; DE; FG; FH;GH; csúcsok éllel összekötve. Szintén indirekten bizonyítsunk, tfh: ki tudjuk választani a 8 csúcsból a négy rosszat, úgy, hogy a fenti 7 él között ne legyen jó! Ekkor CDE háromszögben a 3 csúcsból legalább kettő rossz, ellenkező esetben lenne a háromszögben jó él! Ugyanez igaz FGH háromszögre. Tehát C;D;E;F;G;H csúcsok közül legalább 4 csúcs rossz. Azaz a négy rossz csúcs ezen hat csúcs közt van.Tehát A és B csúcsok jók, azaz AB él jó!

Ha valakinek sikerült az ehavi utolsó B-s feladatot(ha jól emlékszem B.3671.) megoldani, szívesen megnézném, mert bajlódtam vele, de nem jött ki.

Már regisztráltál?
Új vendég vagy?