| [933] Kovács 972 Márton | 2014-11-11 17:04:40 |
 Köszönöm szépen ezt is, de nekem továbbra is az a sejtésem, hogy ezt meg lehet oldani, valami szép, elemi úton is. :)
Pld.: tükrözések összességével, invariáns tulajdonság keresésével, esetleg valamiféle indukció, vagy akármi hasonló trükk segítségével.
|
| Előzmény: [931] w, 2014-11-11 16:09:33 |
|
| [932] Fálesz Mihály | 2014-11-11 16:39:19 |
 Mondjuk a maximum-elvre hivatkozni sokkal "meredekebb", mint a Hadamard-egyenlőtlenség... ;-)
Szerencsére polinomokra a maximum-elv bizonyítása is sokkal egyszerűbb.
|
| Előzmény: [931] w, 2014-11-11 16:09:33 |
|
|
| [930] Kovács 972 Márton | 2014-11-11 15:03:02 |
 Köszönöm szépen mind a két megoldást!
A B.4655 feladat megoldása szép, sajnos más irányokba indultam el, így nem jött ez ki nekem.
A B.4659 feladatra adott megoldás pedig első olvasatra elég meredek (még másodikra is), de elolvasom a 2 cikket amit írtál melléjük.
Nagyon sokat foglalkoztam ezzel a feladattal, ezért az alábbi dolog igazolása érdekelne: (én nem tudok vele dűlőre jutni)
1. Lássuk be, hogy a pontoknak a köríven kell lennie. 2. Egyenletes eloszlásban. 3. Ekkor kiszámolni.
Ez a 3 állítás együttesen kihozná a feladat állítását, és a &tex;\displaystyle (\sqrt{n})^n&xet; maximumot is.
A 2-es és 3-as pontot meg tudom csinálni. Az 1-es nem megy. Ebben tudna valaki segíteni?
|
|
| [929] Fálesz Mihály | 2014-11-11 11:19:30 |
 A B.4655. az
&tex;\displaystyle x^2+y^2 = 8\cdot 2012^{2015}+2 &xet;
egyenletre vezet.
Az &tex;\displaystyle 8\cdot 2012^{2015}+2&xet; szám osztható 7-tel, de nem osztható 49-cel. Viszont &tex;\displaystyle x^2+y^2&xet; csak úgy lehet 7-tel osztható, ha &tex;\displaystyle x&xet; és &tex;\displaystyle y&xet; is osztható 7-tel...
|
| Előzmény: [927] Kovács 972 Márton, 2014-11-11 07:40:32 |
|
| [928] Fálesz Mihály | 2014-11-11 10:40:47 |
 Egy rövid megoldás a B.4659.-re (valószínűleg nem leszel tőle túl boldog, de talán tanulhatsz belőle...):
A pontokat vegyük fel a komplex egységkörben: &tex;\displaystyle a_1,\dots,a_n&xet;. A pontokból készített Vandermonde-determinánsra írjuk fel a Hadamard-egyenlőtlenséget :
&tex;\displaystyle
\left|\prod_{1\le j<k\le n} (a_k-a_j)\right| =
\left| {\rm det} \left(\matrix{
1 & a_1 & a_1^2 & \dots & a_1^{n-1} \cr
1 & a_2 & a_2^2 & \dots & a_2^{n-1} \cr
\dots & \dots & \dots & & \dots \cr
1 & a_n & a_n^2 & \dots & a_n^{n-1} \cr}\right) \right| \le
\prod_{j=1}^n \sqrt{1^2+|a_j|^2+|a_j|^4+\dots+|a_j|^{2n-2}} \le (\sqrt{n})^n.
&xet;
Ha a pontok az egységkörbe írt szabályos &tex;\displaystyle n&xet;-szög csúcsai, akkor egyenlőség áll. Ez közvetlenül is ellenőrizhető, de a megoldásból is leolvasható.
|
| Előzmény: [927] Kovács 972 Márton, 2014-11-11 07:40:32 |
|
| [927] Kovács 972 Márton | 2014-11-11 07:40:32 |
 Sziasztok!
Valaki legyen szíves töltse fel a B.4659 és B.4655 feladatok megoldásait, vagy legalább annak egy vázlatát. Ha megjelenik a honlapon, az is jó, de a szeptemberi feladatok megoldásai sem jelentek meg, én pedig kíváncsi vagyok, hogy hogyan lehet ezeket a feladatokat elegánsan megoldani.
Köszönöm előre is!
Üdv.: Marci
|
|
| [926] w | 2014-11-10 16:59:55 |
 Nos igen. Az eredeti feladatjavaslatnál is kb. ez a megoldás szerepelt, csak, mint pár hónappal később kiderült, ennél sokkal triviálisabb a feladat. :)
Még szóra érdemes az a pici hiba, ahol írod: &tex;\displaystyle n(n-1)(n+1)-1&xet; tényező &tex;\displaystyle 3k+2&xet; alakú, így van &tex;\displaystyle 3k+2&xet; alakú prímosztója. Ez csak &tex;\displaystyle n>1&xet;-re igaz.
|
| Előzmény: [925] emm, 2014-11-10 13:38:26 |
|
| [925] emm | 2014-11-10 13:38:26 |
 &tex;\displaystyle 0>n\implies 0>n^7-n^5-n^4&xet;, s &tex;\displaystyle k^2-k+1>0&xet;, ezért &tex;\displaystyle n>0&xet;. Mivel &tex;\displaystyle -3&xet; kvadratikus nemmaradék mod &tex;\displaystyle p&xet;, ha &tex;\displaystyle p=3k+2&xet;. De &tex;\displaystyle 4(k^2-k+1)=(2k-1)^2+3&xet;. Viszont &tex;\displaystyle 4(n^7-n^5-n^4)=4n^4(n(n-1)(n+1)-1)&xet;-ben az utolsó tényező &tex;\displaystyle 3k+2&xet; alakú, így van &tex;\displaystyle 3k+2&xet; alakú prímosztója. Ellentmondásra jutottunk, nincs megoldás.
|
| Előzmény: [924] w, 2014-11-09 16:46:12 |
|
| [924] w | 2014-11-09 16:46:12 |
 Igen, ez kijön beszorításosan. :) És akkor következik:
B.4643.'' Mely &tex;\displaystyle (n,k)&xet; egész számpárokra teljesül:
&tex;\displaystyle n^7-n^5-n^4=k^2-k+1.&xet;
|
| Előzmény: [923] Róbert Gida, 2014-11-09 15:59:14 |
|
| [923] Róbert Gida | 2014-11-09 15:59:14 |
 Nem számoltam végig, de valószínűleg nincs több. Egy könnyű út: 4 eset van aszerint, hogy n és k milyen előjelű: ha például &tex;\displaystyle n<0; k\ge 0&xet;, akkor &tex;\displaystyle N=-n;K=k&xet; jelöléssel az egyenlet (&tex;\displaystyle N,K\ge 0&xet;)-ra &tex;\displaystyle N^4-N^2+N=K^2-K+1&xet;, itt &tex;\displaystyle K^2-K+1&xet; monoton növő a nemneg. egészeken. De &tex;\displaystyle K=N^2+1&xet;-re &tex;\displaystyle K^2-K+1=N^4+N^2+1>N^4-N^2+N&xet;, továbbá &tex;\displaystyle K=N^2&xet;-re &tex;\displaystyle K^2-K+1=N^4-N^2+1<N^4-N^2+N&xet;, ha &tex;\displaystyle N>1&xet;. Így csak az lehet a monotonitás miatt, hogy &tex;\displaystyle N=0&xet; vagy &tex;\displaystyle N=1&xet; (ez utóbbi ad 2 megoldást). Többi eset is hasonló lehet.
|
| Előzmény: [922] w, 2014-11-09 13:05:50 |
|
|
|
| [920] w | 2014-11-09 11:26:01 |
 B.4643.' Léteznek-e olyan &tex;\displaystyle n&xet; és &tex;\displaystyle k&xet; egész számok, amelyekre &tex;\displaystyle n^4-n^2-n=k^2-k+1&xet;?
|
|
| [919] w | 2014-11-08 15:40:36 |
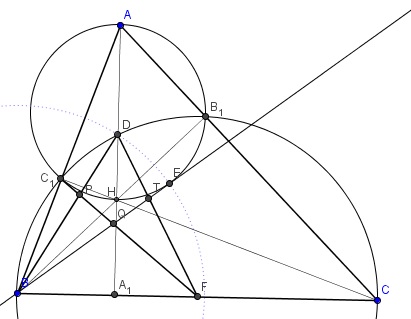
 A.621. Az &tex;\displaystyle ABC&xet; hegyesszögű háromszög magasságainak talppontjai rendre &tex;\displaystyle A_1&xet;, &tex;\displaystyle B_1&xet;, illetve &tex;\displaystyle C_1&xet;. A &tex;\displaystyle BC&xet; oldal felezőpontja &tex;\displaystyle F&xet;. A &tex;\displaystyle BCB_1C_1&xet; pontokon átmenő kör az &tex;\displaystyle AA_1&xet; szakaszt a &tex;\displaystyle D&xet; pontban metszi. Legyen &tex;\displaystyle T&xet; az a pont a &tex;\displaystyle DF&xet; szakaszon, amelyre a &tex;\displaystyle BT&xet; egyenes érinti az &tex;\displaystyle AB_1C_1&xet; kört. Messe a &tex;\displaystyle C_1F&xet; szakasz a &tex;\displaystyle BD&xet; és &tex;\displaystyle BT&xet; egyeneseket &tex;\displaystyle P&xet;-ben, illetve &tex;\displaystyle Q&xet;-ban. Mutassuk meg, hogy a &tex;\displaystyle DPQT&xet; négyszög érintőnégyszög.
Megoldás. &tex;\displaystyle BT&xet; az &tex;\displaystyle E&xet; pontban érinti &tex;\displaystyle AB_1C_1&xet; kört, a magasságpont &tex;\displaystyle H&xet;. Ismert, hogy &tex;\displaystyle AB_1HC_1&xet; húrnégyszög.
Egy, az érintőnégyszögek tételéhez hasonlóan belátható tétel (B.4639. rokona) szerint &tex;\displaystyle DPQT&xet; pontosan akkor érintőnégyszög, hogyha &tex;\displaystyle BD-FD=BQ-FQ&xet; (1).
Könnyű látni, hogy &tex;\displaystyle FC_1B\angle=\beta&xet; és &tex;\displaystyle AC_1B_1\angle=\gamma&xet;, innen &tex;\displaystyle FC_1B_1\angle=\alpha=C_1AB_1\angle&xet;. Ebből leolvasható, hogy &tex;\displaystyle F&xet; az &tex;\displaystyle AB_1C_1&xet; körhöz &tex;\displaystyle C_1&xet;-ben húzható érintőre illeszkedik.
Kaptuk, hogy &tex;\displaystyle QC_1=QE&xet; egyenlő hosszú érintőszakaszok. Ezzel (1) átalakítható:
&tex;\displaystyle BD-FD=BQ-FQ=(BQ+QE)-(FQ+QC_1)=BE-FC_1.&xet;
Mivel &tex;\displaystyle FC_1=FD&xet;, ezért csak annyit kell belátnunk, hogy &tex;\displaystyle BD=BE&xet;.
Invertáljunk a &tex;\displaystyle B&xet; középpontú, &tex;\displaystyle BE&xet; sugarú körre! Ekkor az &tex;\displaystyle AB_1C_1&xet; kör invariáns marad, hisz merőleges az alapkörre, így &tex;\displaystyle A&xet; és &tex;\displaystyle C_1&xet;, &tex;\displaystyle B_1&xet; és &tex;\displaystyle H&xet; helyet cserél. Ezért &tex;\displaystyle AH&xet; egyenes képe &tex;\displaystyle BB_1C_1&xet; kör lesz.
Az inverzióban &tex;\displaystyle D\in AH&xet; képe a &tex;\displaystyle BD&xet; egyenesen lesz, és a &tex;\displaystyle BB_1C_1&xet; körön. Mivel &tex;\displaystyle D&xet; képe &tex;\displaystyle B&xet; nem lehet, ezért &tex;\displaystyle D&xet; fixpont kell legyen. Vagyis &tex;\displaystyle BD=BE&xet;. Ezzel (1)-et beláttuk, készen vagyunk.
|
 |
|
| [918] w | 2014-10-25 20:56:46 |
 Tetszik az a meglátás, hogy a probléma ekvivalens azzal, hogy &tex;\displaystyle BC&xet; oldal hatványvonala az &tex;\displaystyle AB_1C_1&xet; körnek és &tex;\displaystyle D&xet; pontnak.
Innen rövid befejezés kínálkozik a megoldásra.
|
| Előzmény: [917] Sinobi, 2014-10-25 18:18:18 |
|
| [917] Sinobi | 2014-10-25 18:18:18 |
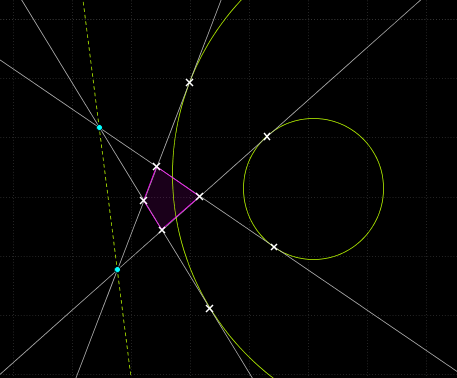
 Az A621-hez egy lemma (az A613-as ha már nem jött ki vele):
Ha két körhöz a hatványvonalán ha felveszünk két pontot, akkor azokból ha érintőket húzunk, a megfelelő érintőegyenesek egy érintőnégyszög oldalai.
A megfordítása meg valami olyasmi, hogy ha az egyik pont nincs a hatványvonalon, akkor a másik pont egy hiperbolán mozog, ha érintőnégyszögeket akarunk kapni (a két körtől való távolságok különbsége állandó).
És akkor azt kell belátni, hogy a B és F pontok az &tex;\displaystyle AB_1C_1&xet; és a D pont hatványvonalán fekszenek.
(nem biztos, hogy így a legegyszerűbb)
Ábra:
|
 |
|
| [916] Old boy | 2014-10-24 06:57:12 |
 Egy megjegyzés a C. 1242. feladathoz. Nemcsak derékszögű, hanem bármilyen háromszögre érvényes a következő tétel. Az alábbi három állítás közül 1) az egyenes felezi a háromszög kerületét 2) az egyenes felezi a háromszög területét 3) az egyenes átmegy a beírt kör középpontján ha bármelyik kettő mint feltétel igaz, akkor a harmadik is, mint állítás igaz. A kitűzött feladatra vonatkozólag ez azt jelenti, hogy a megoldásként kapott „felező egyenes” is átmegy a háromszög beírható körének középpontján. A feladat speciális adataival ez kis számolással a fenti tétel ismerete nélkül is igazolható. A beírt kör sugarát r-el jelölve a terület: T = a*r/2+b*r/2+c*r/2 = r/2*(a+b+c). Mivel T = 6 és a+b+c = K = 12, 6 = r/2 * 12, amiből r = 1. Ezek után helyezzük el a háromszöget a (derékszögű) koordináta rendszerben úgy, hogy a derékszögnél levő csúcsot az origóra, a befogókat a két tengelyre fektetjük (az első síknegyedben). Ekkor a beírt kör középpontja a P(1;1) pont lesz. A megoldásban kapott értékekkel felírva a két adott ponton átmenő egyenes egyenletét láthatjuk, hogy P koordinátái kielégítik az egyenletet, azaz az egyenes valóban átmegy a P ponton.
|
|
| [915] Sinobi | 2014-10-23 01:20:45 |
 Való igaz, gyakran jól jönne a sokkal hamarabbi megoldás. Főleg amikor (egy iskolában mondjuk) senki nem tudja megcsinálni. A hivatalos később már nem ér sokat.
Talán az lenne a legkézenfekvőbb megoldás, ha a feladatot beküldők beküldéskor egy checkbox-szerűvel hozzájárulnhatnának ahhoz hogy a beküldött megoldás pl a munkafüzetbe regisztrált tagok számára látható legyen. (azt hiszem ha nem nagyon ocsmány az e-KöMaL kódja akkor nem kell sokat kalapálni egy ilyen beépítéséhez rajta)
|
| Előzmény: [913] microprof2, 2014-10-22 10:39:46 |
|
| [914] w | 2014-10-22 18:53:57 |
 Akkor kimásolom neked a megoldásokat:
B.4647. Legyen a &tex;\displaystyle 100&xet; egységkör halmaza &tex;\displaystyle K&xet;, továbbá a &tex;\displaystyle K&xet; körei által lefedett &tex;\displaystyle 101&xet;-edik egységkör &tex;\displaystyle k&xet;.
Válasszuk ki &tex;\displaystyle K&xet;-ból azt a &tex;\displaystyle c&xet; kört, amely lefedi &tex;\displaystyle k&xet;-nak a legalsó pontját; legyen &tex;\displaystyle k&xet; és &tex;\displaystyle c&xet; középpontja &tex;\displaystyle O&xet; és &tex;\displaystyle C&xet;, &tex;\displaystyle k&xet; legalsó pontja &tex;\displaystyle B&xet;, &tex;\displaystyle c&xet; legfelső pontja &tex;\displaystyle A&xet;. Mivel &tex;\displaystyle BO=CA=1&xet; függőleges szakaszok, így &tex;\displaystyle AOBC&xet; paralelogramma, amiből &tex;\displaystyle OA=CB&xet;. Mivel viszont &tex;\displaystyle c&xet; lefedi &tex;\displaystyle B&xet;-t, így &tex;\displaystyle CB\le 1&xet;, ahonnan &tex;\displaystyle OA\le 1&xet;, ami ekvivalens azzal, hogy &tex;\displaystyle k&xet; lefedje &tex;\displaystyle A&xet; pontot.
Tegyük fel indirekt, hogy &tex;\displaystyle K^*:=K\setminus\{c\}&xet; nem tartalmaz olyan kört, amely lefedi &tex;\displaystyle A&xet; pontot. Ekkor a &tex;\displaystyle K^*&xet;-beli körök középpontjainak távolsága &tex;\displaystyle A&xet;-tól mind &tex;\displaystyle 1&xet;-nél nagyobb. Legyen e véges sok távolság közül a legkisebbik &tex;\displaystyle d>1&xet;, ekkor minden &tex;\displaystyle K^*&xet;-beli középpont legalább &tex;\displaystyle d&xet; távol van &tex;\displaystyle A&xet;-tól, vagyis a &tex;\displaystyle K^*&xet;-beli körök minden pontja legalább &tex;\displaystyle d-1&xet; messzire esik az &tex;\displaystyle A&xet; ponttól.
Legyen &tex;\displaystyle P&xet; a &tex;\displaystyle k&xet; körnek legfelső pontja, és tekintsük az &tex;\displaystyle AP&xet; szakaszt (ez a szakasz létezik, hisz &tex;\displaystyle A\neq P&xet; mert &tex;\displaystyle c\neq k&xet; feltétel volt). Mivel &tex;\displaystyle A&xet; és &tex;\displaystyle P&xet; is &tex;\displaystyle k&xet; határán vagy belsejében van, ezért a kör konvexitása miatt &tex;\displaystyle AP&xet; szakasz &tex;\displaystyle k&xet; belsejébe esik. Mi több, a &tex;\displaystyle P&xet; pont magasabban helyezkedik, mint &tex;\displaystyle A&xet;, mert &tex;\displaystyle O&xet; magasabban van &tex;\displaystyle C&xet;-nél, tudniillik &tex;\displaystyle BC\le 1&xet; miatt &tex;\displaystyle C\neq O&xet; a &tex;\displaystyle B&xet; középpontú egységkörlapra esik, amely körlap legfelső pontja &tex;\displaystyle O&xet;. Tehát &tex;\displaystyle A&xet; kivételével az &tex;\displaystyle AP&xet; szakaszon lévő pontok mind &tex;\displaystyle c&xet; felett találhatók, így &tex;\displaystyle c&xet; nem tartalmazza őket.
Válasszunk az &tex;\displaystyle AP&xet; szakaszon egy olyan &tex;\displaystyle X&xet; pontot, amelyre &tex;\displaystyle 0<AX<d-1&xet;. Ekkor az &tex;\displaystyle X&xet; pontot &tex;\displaystyle c&xet; körlap nem tartalmazza, továbbá mivel feltevésünk szerint a &tex;\displaystyle K^*&xet;-beli körök minden pontja legalább &tex;\displaystyle d-1&xet; messze van &tex;\displaystyle A&xet;-tól, így azok sem fedik le &tex;\displaystyle X&xet; pontot. Vagyis &tex;\displaystyle X&xet; olyan pont &tex;\displaystyle k&xet; belsejében, amit egyik &tex;\displaystyle K&xet;-beli kör sem fed le, ez ellentmond a feltételnek.
Tehát van olyan &tex;\displaystyle K^*&xet;-beli kör, amely tartalmazza &tex;\displaystyle c&xet; legfelső &tex;\displaystyle A&xet; pontját. Ez bizonyítja a feladat állítását.
B.4549. Tegyük fel, hogy &tex;\displaystyle f_1&xet;, &tex;\displaystyle f_2&xet; és &tex;\displaystyle f_3&xet; egyenesek párhuzamosak, úgy helyezkednek el, hogy &tex;\displaystyle f_2&xet; esik az &tex;\displaystyle f_1&xet; és &tex;\displaystyle f_3&xet; egyenesek közé, és elmetszik az &tex;\displaystyle e_1,e_2,\dots,e_n&xet; egyenesek mindegyikét. Legyen &tex;\displaystyle f_1&xet;, &tex;\displaystyle f_2&xet;, &tex;\displaystyle f_3&xet; és &tex;\displaystyle e_i&xet; metszéspontja rendre &tex;\displaystyle A_i&xet;, &tex;\displaystyle B_i&xet;, &tex;\displaystyle C_i&xet; minden &tex;\displaystyle 1\le i\le n&xet;-re, és a megfelelő pontokba egy tetszőleges &tex;\displaystyle O&xet; origóból mutató helyvektorok &tex;\displaystyle \vec{a_i}&xet;, &tex;\displaystyle \vec{b_i}&xet; és &tex;\displaystyle \vec{c_i}&xet;.
Legyen továbbá &tex;\displaystyle \lambda:=\frac{d(f_3,f_1)}{d(f_2,f_1)}&xet;. A párhuzamos szelők tétele szerint ekkor &tex;\displaystyle \frac{A_iC_i}{A_iB_i}=\lambda&xet; (bármely &tex;\displaystyle i=1,\dots,n&xet;-re). Mivel pedig &tex;\displaystyle A_i,B_i,C_i&xet; kollineáris és &tex;\displaystyle B_i&xet; az &tex;\displaystyle A_iC_i&xet; szakaszra esik, hisz &tex;\displaystyle f_2&xet; van &tex;\displaystyle f_1&xet; és &tex;\displaystyle f_3&xet; között, így ezt úgy is írhatjuk, hogy &tex;\displaystyle \vec{A_iC_i}=\lambda\cdot \vec{A_iB_i}&xet;, azaz &tex;\displaystyle \vec{c_i}-\vec{a_i}=\lambda\left(\vec{b_i}-\vec{a_i}\right)&xet;. &tex;\displaystyle (*)&xet;
Jelölje az &tex;\displaystyle A_1,\dots,A_n&xet; pontok &tex;\displaystyle S_A&xet;, a &tex;\displaystyle B_1,\dots,B_n&xet; pontok &tex;\displaystyle S_B&xet;, illetve a &tex;\displaystyle C_1,\dots,C_n&xet; pontok &tex;\displaystyle S_C&xet; súlypontjába mutató helyvektort rendre &tex;\displaystyle \vec{s_a}&xet;, &tex;\displaystyle \vec{s_b}&xet;, &tex;\displaystyle \vec{s_c}&xet;. Ekkor &tex;\displaystyle (*)&xet; értelmében, és persze felhasználva a súlypont definícióját, felírhatjuk a következőt:
&tex;\displaystyle \vec{S_AS_C}=\vec{s_c}-\vec{s_a}=\frac1n\sum_{i=1}^n \vec{c_i}-\frac1n\sum_{i=1}^n \vec{a_i}=\frac1n\sum_{i=1}^n \left(\vec{c_i}-\vec{a_i}\right)=&xet;
&tex;\displaystyle =\frac1n\sum_{i=1}^n \lambda\left(\vec{b_i}-\vec{a_i}\right)=\lambda\cdot \left(\frac1n\sum_{i=1}^n \vec{b_i}-\frac1n\sum_{i=1}^n \vec{a_i}\right)=\lambda\cdot \left(\vec{s_b}-\vec{s_a}\right)=\lambda\cdot\vec{S_AS_B},&xet;
amiből tüstént leolvasható, hogy az &tex;\displaystyle S_C&xet; pont az &tex;\displaystyle S_AS_B&xet; egyenesre esik.
A feladat megoldásához azt kell belátnunk, hogy az összes &tex;\displaystyle S_\alpha&xet; pont egy egyenesre esik. Ehhez persze elegendő belátni, hogy bármely három &tex;\displaystyle S_\alpha&xet; pont egy egyenesen van, hisz akkor minden &tex;\displaystyle S_\alpha&xet; pont illeszkedik valamely két &tex;\displaystyle S_\alpha&xet; pont által meghatározott egyenesre. Utóbbi tényt azonban a fenti okfejtéssel bebizonyítottuk, így készen is vagyunk.
|
| Előzmény: [913] microprof2, 2014-10-22 10:39:46 |
|
| [913] microprof2 | 2014-10-22 10:39:46 |
 Köszönöm, de főleg utóbbi nem sokat segített. Arra, hogy vektorok kellenének meg hogy ki kéne használni a párhuzamosságot, eddig is gondoltam. Csak hozzá sem tudok kezdeni. Nem lenne baj, ha a 6 pontos feladatok megoldása aránylag hamar megjelenne online.
|
| Előzmény: [912] w, 2014-10-15 15:28:15 |
|
| [912] w | 2014-10-15 15:28:15 |
 B.4647. Van 100 egységkörünk, ezek halmaza legyen &tex;\displaystyle K&xet;, és még van egy 101., amit együttesen lefednek, ez legyen &tex;\displaystyle k&xet;.
Mi garantálná azt, hogy legyen olyan &tex;\displaystyle c\in K&xet; kör, amelynek a legfelső pontja le van fedve &tex;\displaystyle K&xet; többi köre által? Legegyszerűbben úgy lehetne ezt elérni, hogyha &tex;\displaystyle c&xet; legfelső pontja netán &tex;\displaystyle k&xet;-ba esne, hisz már van olyan feltételünk, hogy &tex;\displaystyle k&xet;-t lefedik &tex;\displaystyle K&xet; körei.
A megoldáshoz szerintem elég lesz a következő két kulcslépést belátnod:
1. állítás: &tex;\displaystyle k&xet; pontosan akkor tartalmazza &tex;\displaystyle c&xet; legfelső pontját, hogyha &tex;\displaystyle c&xet; lefedi &tex;\displaystyle k&xet; legalsó pontját.
2. állítás: legyen &tex;\displaystyle k&xet; legfelső pontja &tex;\displaystyle P&xet;, és &tex;\displaystyle c&xet; legfelső pontja &tex;\displaystyle A&xet;. Ekkor &tex;\displaystyle AP&xet; szakasz belső pontjait &tex;\displaystyle k&xet; lefedi, de &tex;\displaystyle c&xet; nem.
B.4649. Vektorok és a párhuzamos szelők tétele segítségével bizonyítsd be, hogy az említett súlypontok közül bármely három egy egyenesre esik.
|
| Előzmény: [911] microprof2, 2014-10-15 14:27:29 |
|
| [911] microprof2 | 2014-10-15 14:27:29 |
 Valaki tudna mondani egy szép megoldást a B4647 és B4649 feladatokra? Előre is kösz.
|
|
| [910] Róbert Gida | 2014-10-13 14:02:57 |
 A622. potya feladat volt (hivatalos megoldás is fent van.)
&tex;\displaystyle 7^{7*h}+1=(7^h+1)*L*M&xet;, ahol
&tex;\displaystyle L=T^3-B, M=T^3+B, T=7^h+1, B=7^k*(T^2-7^h), h=2k-1&xet;
Így már &tex;\displaystyle \frac {7^{7*h}+1}{7^h+1}&xet; is összetett, ha &tex;\displaystyle h&xet; páratlan szám. Egyébként Aurifeuillean faktorizáció a neve. Aki ezt ismeri az kb. 1 perc alatt meg is oldotta. Más alapokra, kitevőkre is van hasonló faktorizáció, ez mind ismert, és valószínűtlen, hogy lenne más felbontás is.
|
|
| [909] w | 2014-08-10 14:11:39 |
 Ami nekem szintetikus úton kijött az A.614. feladatból a következő, önmagában is érdekes feladat.
Legyen &tex;\displaystyle ABC&xet; háromszög &tex;\displaystyle BC&xet; oldalához írt köre &tex;\displaystyle h&xet;, amely a &tex;\displaystyle BC&xet; oldalt &tex;\displaystyle D&xet;-ben érinti. Tekintsük azt a &tex;\displaystyle k&xet; kört, amely áthalad a &tex;\displaystyle B&xet; és &tex;\displaystyle C&xet; pontokon, és érinti &tex;\displaystyle h&xet;-t (de nem a &tex;\displaystyle BC&xet; egyenes). Mutassuk meg, hogy &tex;\displaystyle h&xet; és &tex;\displaystyle k&xet; érintési pontját &tex;\displaystyle P&xet;-vel jelölve, &tex;\displaystyle PD&xet; egyenes felezi a &tex;\displaystyle BPC&xet; szöget.
|
|








