| [858] GK | 2013-12-16 11:13:48 |
 hello!
A novemberi feladatok (matek, k jelű) megoldásai hol olvashatók?
|
|
| [857] HoA | 2013-12-13 14:13:27 |
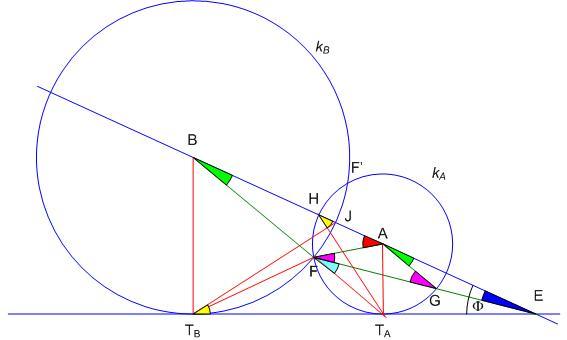
 De előbb [856] utolsó képletein felbátorodva egy elemi megoldás:
F tükörképe v1 -re F’ . FF’ látószöge az A, B , E pontokból rendre 4 ,4 ,4 ,4 ,4 . EF másik metszéspontja kA -val G. Mivel E kA és kB külső hasonlósági pontja, EAG . EF másik metszéspontja kA -val G. Mivel E kA és kB külső hasonlósági pontja, EAG =2 =2 . EAG és FAG . EAG és FAG 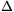 ekből ekből
 - - =2 =2
v1 metszéspontja kA val ill. kB vel A és B között H ill. J. A HATA és JBTB 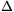 ekből ekből 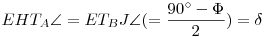 . FTBE . FTBE = = - - EFTA EFTA = =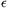 ra EFTAH hurkolt négyszögből ra EFTAH hurkolt négyszögből 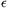 + + = = +2 +2 , ,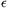 = = +2 +2 - - = = - - =FTBE =FTBE . EFTAésETBF . EFTAésETBF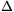 ek hasonlók. ETA.ETB=EF2 Hasonlóan ugyanezt kapjuk ETC.ETD re. Így TA,TB,TC,TD, egy körön vannak és ETA=EA.cos ek hasonlók. ETA.ETB=EF2 Hasonlóan ugyanezt kapjuk ETC.ETD re. Így TA,TB,TC,TD, egy körön vannak és ETA=EA.cos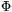 stb. matt A, B, C, D is. stb. matt A, B, C, D is.
|
 |
| Előzmény: [856] Fálesz Mihály, 2013-12-13 07:47:25 |
|
| [856] Fálesz Mihály | 2013-12-13 07:47:25 |
 Van teljesen koordináta-geometriai megoldás is.
Legyen d1(X) és d2(X) a két vezéregyenestől mért előjeles távolság. A metszéspontokra teljesül például a következő egyenlet:
FX2=d12(X)+d22(X).
Innen ti jöttök.
|
| Előzmény: [855] w, 2013-12-12 17:45:26 |
|
| [855] w | 2013-12-12 17:45:26 |
 Ez szép megoldás. Mivel viszont a decemberi Kömalban a feladatot koordinátageometria kategóriába sorolták, érdemes volna egy ilyen megoldást is megemlíteni, én például így csináltam.
Ha d1 és d2 párhuzamos, akkor kész vagyunk, tegyük fel, hogy nem párhuzamosak. Legyen O=d1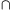 d2, legyen olyan koordinátarendszerünk, melyben d1 az x-tengely és O az origó. d2, legyen olyan koordinátarendszerünk, melyben d1 az x-tengely és O az origó.
Megmutatjuk, hogy 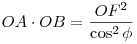 , ahol , ahol  a d1 és d2 egyenesek szöge. Legyen F(p,q), és legyen d2 egyenlete y=mx. Ekkor az ismert képletek szerint tetszőleges (x,y) pont távolsága d2-től a d1 és d2 egyenesek szöge. Legyen F(p,q), és legyen d2 egyenlete y=mx. Ekkor az ismert képletek szerint tetszőleges (x,y) pont távolsága d2-től 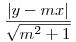 , távolsága F-től pedig , távolsága F-től pedig 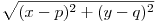 , a P2 parabola (x,y) pontjaira ez a két mennyiség megegyezik, azaz , a P2 parabola (x,y) pontjaira ez a két mennyiség megegyezik, azaz
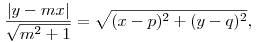
![(y-mx)^2=(m^2+1)\left[(x-p)^2+(y-q)^2\right].](keplet.cgi?k=2B891C101F16B6DE)
Mivel A és B második koordinátája nulla, így első koordinátáikra, x1 és x2-re másodfokú egyenletet kapunk:
![(mx)^2=(m^2+1)\left[(x-p)^2+q^2\right]](keplet.cgi?k=E41AEF7F97FAA074)
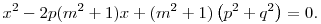
A Viéte-formulákból adódik, hogy 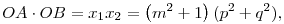 ahol OF2=p2+q2 és m=tg ahol OF2=p2+q2 és m=tg  , ezért az állításunkat igazoltuk. Ugyanezzel egyenlő OC.OD, ha a d2 egyenest vesszük x-tengelynek. Mivel P1 a d1 és P2 a d2 egyenes felett halad, így O az AB és CD szakaszok külső pontja, és így A,B,C,D konciklikus. , ezért az állításunkat igazoltuk. Ugyanezzel egyenlő OC.OD, ha a d2 egyenest vesszük x-tengelynek. Mivel P1 a d1 és P2 a d2 egyenes felett halad, így O az AB és CD szakaszok külső pontja, és így A,B,C,D konciklikus.
|
| Előzmény: [854] HoA, 2013-12-12 10:04:17 |
|
| [854] HoA | 2013-12-12 10:04:17 |
 Nem euklideszi [76] –nál talán egyszerűbb megoldás A.599 -re:
A. 599. A P1 és P2 parabolák fókuszpontja közös. A P1 vezéregyenese a P2-t az A és B pontokban, a P2 vezéregyenese pedig a P1-et az C és D pontokban metszi. Mutassuk meg, hogy az A, B, C és D pontok egy körön vannak.
1: A közös fókusz F, a v1 és v2 vezéregyenesek az E ponban  szögben metszik egymást.Az A ill. B középpontú , F-en átmenő kA ill. kB körök v2-t TA-ban ill. TB -ben érintik. Hasonlóan a C ill. D középpontú , F-en átmenő kC ill. kD körök v1-et TC-ben ill. TD -ben érintik.Bizonyítandó, hogy EA.EB=EC.ED . szögben metszik egymást.Az A ill. B középpontú , F-en átmenő kA ill. kB körök v2-t TA-ban ill. TB -ben érintik. Hasonlóan a C ill. D középpontú , F-en átmenő kC ill. kD körök v1-et TC-ben ill. TD -ben érintik.Bizonyítandó, hogy EA.EB=EC.ED .
2: Mivel P = A, B, C, D –re igaz, hogy ETP=EP.cos , ez pontosan akkor teljesül, ha ETA.ETB=ETC.ETD , vagyis ha a TP pontok egy körön vannak. , ez pontosan akkor teljesül, ha ETA.ETB=ETC.ETD , vagyis ha a TP pontok egy körön vannak.
3: Egy F középpontú inverzió v1 -et és v2 -t az F-en átmenő, O1’ ill. O2’ középpontú v1’ ill. v2’ körökbe, az F-en átmenő, v1 -et merőlegesen metsző, v2-t érintő kA és kB köröket a v1’ -t merőlegesen metsző, tehát O1’ -n átmenő, v2’ -t érintő egyenesekbe, az F-en átmenő, v2 -t merőlegesen metsző, v1-t érintő kC és kD köröket a v2’ -t merőlegesen metsző, tehát O2’ -n átmenő, v1’ -t érintő egyenesekbe képezi le.
4: TA’,TB’,TC’,TD’ rajta vannak O1’O2’ Thálesz körén, ezért az eredeti TP pontok is egy körön vannak, és így (2) alapján A,B,C,D is.
|
|
| [853] Róbert Gida | 2013-11-24 19:52:15 |
 Wolfram Alpha kitalálja nekünk a sorozatot, csak az első 4 tag kell neki:
FindSequenceFunction[{ { 2,1/8 }, { 3,1/6 } , { 4,3/16 }, {5,1/5 } } , n]
|
| Előzmény: [852] w, 2013-11-23 23:56:53 |
|
| [852] w | 2013-11-23 23:56:53 |
 Két megjegyzésem volna.
1. Az 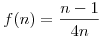 képletet megsejteni annyira nem triviális, de egyetértek, csak 5 pontot érne. képletet megsejteni annyira nem triviális, de egyetértek, csak 5 pontot érne.
2. A megadott rekurziót meg lehet oldani sejtés nélkül. Elég ehhez átrendezni: 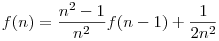 ekvivalens ekvivalens 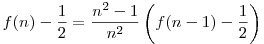 -vel. Innen teleszkópikus szorzat. Ezen megoldás viszont csak a hiv. megoldás egyszerűbb átfogalmazása. -vel. Innen teleszkópikus szorzat. Ezen megoldás viszont csak a hiv. megoldás egyszerűbb átfogalmazása.
|
| Előzmény: [850] Róbert Gida, 2013-11-23 22:09:21 |
|
|
|
| [849] w | 2013-11-15 21:29:51 |
 Igen, én is ezt csináltam. Kis megjegyzés az érdeklődők számára, akiknek nem ismert, amit felhasználtunk. Valójában két dologra volt szükség:
(1) (Fn,Fk)=F(n,k),
(2) p|Fp-1 vagy p|Fp+1. /p prím/
Az (1) bizonyításához a kulcs a Fibonacci számok bontogatásával adódó azonosság lehet: Fn=Fn-1+Fn-2=2Fn-2+Fn-3=...=FiFn-i+1+Fi-1Fn-i. Ebből indukcióval előbb n|k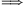 Fn|Fk adódik, majd maga az (1). Fn|Fk adódik, majd maga az (1).
A (2) bizonyítása nehezebb, és attól függ, hogy 5(p-1)/2 +1 vagy -1 maradékot ad mod p. Ha utóbbi a helyzet, akkor p|Fp+1, ennek belátásához elég kifejteni a binomiális tétellel az Fp+1-re vonatkozó explicit képletet. Az előbbi eset érdekesebb, abban az esetben az 5 kvadratikus maradék lesz mod p (lásd pl. itt), ezért  és és  reprezentálható, mint maradék mod p, vagyis a Binet-képlet felírható mod p maradékokkal is, és p|Fp-1 a Kis-Fermat-tételből következik. (Amúgy itt is van erről szó.) Szóval ezzel a két lemma is elintézhető. reprezentálható, mint maradék mod p, vagyis a Binet-képlet felírható mod p maradékokkal is, és p|Fp-1 a Kis-Fermat-tételből következik. (Amúgy itt is van erről szó.) Szóval ezzel a két lemma is elintézhető.
Ha tud valaki jobb bizonyítást, az érdekelne.
|
| Előzmény: [848] Róbert Gida, 2013-11-15 20:49:35 |
|
| [848] Róbert Gida | 2013-11-15 20:49:35 |
 Valóban, ezt a példát akkor elvinném:
(lejárt) A598. megoldása:
Legyen Fn az n-edik Fibonacci szám. Ismert, hogy lnko(Fn,Fk)=Flnko(n,k) ebból kapjuk, hogy az m-el osztható Fibonacci számok pontosan (valamilyen t-re) a t-vel osztható indexűek, ezen t pedig akkor nyilván a legisebb pozitív egész, amire Ft osztható m-mel (t létezik). Ismert, hogy m=p-re t|p+-1, ha p!=5 (valójában p-nek az ötös maradékától függ, hogy p+1 vagy p-1, de ez itt most nem kell).
A feladat a,b,c-ben ciklikus. Tegyük fel, hogy az egyik páros, mondjuk az a. 2|a, akkor 2|Fb, így 3|b, de akkor 3|Fc, így 4|c, amiből 4|Fa, így 6|a is teljesül, végül 6|Fb miatt 12|b. Innen pedig 12|c, majd 12|a következik. Azaz 12|a,b,c, ami az egyik lehetőség volt.
Ha van köztük 5-tel osztható, akkor például 5|a, de akkor 5|Fb, amiből 5|b és hasonlóan 5|c is kijön. Azaz 5|a,b,c, a másik lehetőség,
Ha nincs köztük páros és 5-tel osztható sem, akkor p legyen az a,b,c legkisebb prímosztója (ilyen van, mert a,b,c>1) ami nem lehet a 2 sem az 5, ekkor mondjuk p|a, így p|Fb, de mivel ekkor p|F(p+-1) (lásd fent). Így p|Flnko(p+-1,b), de p minimalitása miatt lnko(p+-1,b)=1, vagy p=2. Első esetben p|F1=1, ellentmondás, második esetben b páros, szintén ellentmondás.
|
| Előzmény: [847] w, 2013-11-13 17:29:47 |
|
|
| [846] w | 2013-10-29 19:44:42 |
 Tehát az én megoldásom (vázlatos):
Vegyük észre, hogy
a) a1+a2+...+a2013=2014
b) a1+2a2+...+2013a2013=4026.
Emellett vezessük be ak-t, mint a legutolsó olyan ai szám a mondatban, ami még nem nulla. Mivel minden szám legfeljebb k-szor fordul elő a mondatban, és a nullák száma legalább 2013-k, így k 2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak. 2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak.
Vonjuk ki a)-t b)-ből, amit kapunk, azt pedig becsüljük meg alulról:
![2012=\sum_{i=2}^k (i-1)a_i=\sum_{i=2}^{k-1}(i-1)a_i+ka_k\ge[1+2+\dots+(2011-k)]+k=[1+2+\dots+(2010-k)]+2011](keplet.cgi?k=FCA691FC5F319BCB)
Ebből adódik, hogy k>2008 is igaz. Innen kis gondolkodás és kész.
|
| Előzmény: [844] w, 2013-10-21 21:05:42 |
|
| [845] Róbert Gida | 2013-10-23 21:22:38 |
 Aki a feltett megoldásokat elolvassa nagy előnyben van: http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=A588&l=hu
http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=A595&l=hu
|
|
| [844] w | 2013-10-21 21:05:42 |
 Talán a legnehezebb szeptemberi B-feladat (legalábbis számomra) a B.4552-es volt:
Ebben a mondatban az 1 alkalommal előforduló számok száma a1,
a 2 alkalommal előforduló számok száma a2,
...,
a 2013 alkalommal előforduló számok száma a2013.
Adjuk meg az a1,a2,...,a2013 számokat úgy, hogy igaz állítást kapjunk. Hányféleképpen tehetjük ezt meg?
Hogyan oldottátok meg? (Nekem van egy relatívan szép és egyszerű megoldásom, de kíváncsi vagyok, hogy Ti mit kezdettetek vele. Az eredeti javasolt megoldás is érdekelne.)
|
|
|
|
|
| [840] Kardos | 2013-10-17 20:57:57 |
 B. 4559.-hez van valakinek valami ötlete?!?!? :) Előre is köszi!
|
|
| [839] n | 2013-10-13 17:49:17 |
 Azért az A595-höz a kétnégyzetszámos bizonyítás se' annyira ötlet, mert kb. rögtön kipotyog belőle a megoldás...
|
| Előzmény: [838] w, 2013-10-13 15:18:16 |
|
|
| [837] w | 2013-10-11 10:48:27 |
 Igen. (Pontosítás: k+1 pont határoz meg egy k fokszámú polinomot.)
Nyilván az volt a háttérbeli cél, hogy belássuk, hogyha érvényes a megadott feltétel, akkor a két polinom csak egymás eltoltja lehet. A következő kérdésem tehát az volna, hogyha deg(P)=deg(Q)=n, a feltétel marad, és P(x) Q(x+k) (k>0), akkor mekkora lehet k? Q(x+k) (k>0), akkor mekkora lehet k?
|
| Előzmény: [836] Sinobi, 2013-10-11 10:41:18 |
|
| [836] Sinobi | 2013-10-11 10:41:18 |
 Nem léteznek. Egy idő után mind a kettő monoton lesz (legyen monoton növő), és nagyobb az addigi felvett értékeknél.
Ebből következik, hogy egy idő után ha p(x)=q(z), akkor p(x+n)=q(z+n), minden természetes n-re. Legyen p és q közül a nagyobb fokszma k. Mivel k pontra egyértelműen illeszthető k (vagy annál kisebb, ha létezik) fokszámú polinom, véve az (x,p(x)), (x+1,p(x+1)),...(x+k,p(x+k)) és (z,q(z)), (z+1,q(z+1)),...(z+k,q(z+k)) pontokat, ezek egyértelműen meghatározzák p-t, és q-t is, és ezek a pontok egymásba eltolhatóak, tehát p és q is egymásba eltolható, tehát ugyanannyi a fokszámuk, ha léteznek.
|
| Előzmény: [835] w, 2013-10-11 10:25:59 |
|
| [835] w | 2013-10-11 10:25:59 |
 B.4561-hez egy nehéz, de nagyon érdekes csatlakozó kérdés:
Léteznek-e olyan különböző fokszámú P és Q polinomok, melyeknek természetes számokon vett értékkészleteik megegyeznek?
|
|
| [834] w | 2013-07-07 08:32:26 |
 Melyik a könnyebb: B.4149 vagy B.4536? Érdekes, hogy az ilyen ismétlődő feladatokat akkor találjuk meg, mikor legkevésbé keressük őket :-) A megfogalmazást, a hiv. megoldás hosszát és a statisztikát is érdemes megfigyelni.
|
|




 ,4
,4 ,4
,4 . EF másik metszéspontja kA -val G. Mivel E kA és kB külső hasonlósági pontja, EAG
. EF másik metszéspontja kA -val G. Mivel E kA és kB külső hasonlósági pontja, EAG =2
=2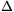 ekből
ekből  -
-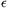 ra EFTAH hurkolt négyszögből
ra EFTAH hurkolt négyszögből 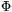 stb. matt A, B, C, D is.
stb. matt A, B, C, D is. 


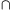 d2, legyen olyan koordinátarendszerünk, melyben d1 az x-tengely és O az origó.
d2, legyen olyan koordinátarendszerünk, melyben d1 az x-tengely és O az origó.  a d1 és d2 egyenesek szöge. Legyen F(p,q), és legyen d2 egyenlete y=mx. Ekkor az ismert képletek szerint tetszőleges (x,y) pont távolsága d2-től
a d1 és d2 egyenesek szöge. Legyen F(p,q), és legyen d2 egyenlete y=mx. Ekkor az ismert képletek szerint tetszőleges (x,y) pont távolsága d2-től 
 Fn|Fk adódik, majd maga az (1).
Fn|Fk adódik, majd maga az (1).  2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak.
2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak. 


 Q(x+k) (k>0), akkor mekkora lehet k?
Q(x+k) (k>0), akkor mekkora lehet k?