Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Fórum: Lejárt határidejű KÖMAL feladatokról

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]  

Szeretnél hozzászólni? Jelentkezz be.
[433] S.Ákos2008-12-22 10:21:56

Arra nem figyeltél, hogy nem ugyanakkora a valószínűsége az eseményeknek.

Előzmény: [432] Blinki Bill, 2008-12-22 09:16:59
[432] Blinki Bill2008-12-22 09:16:59

Kedves Fórumozók!

A C.958. számú feladatra az alábbi megoldást adtam. Kérlek, ha van egy kis időtök, akkor mondjátok meg, hogy mi a hiba benne, mert egészen más eredményt kaptam, mint a hivatalos megoldás.

Előre is kösz.

Számoljuk össze a lehetséges játék-befejeződéseket:

1dobásból vége van a játéknak: 4est dobunk, vagy 5-öst dobunk vagy 6-ost dobunk, azaz 3 eset összesen

2dobásból van vége a játéknak: 1-3;1-4;1-5;1-6; 2-2;2-3;2-4;2-5;2-6; 3-1;3-2;3-3;3-4;3-5;3-6, azaz 15 eset összesen

3dobásból van vége a játéknak: 1-1-2;1-1-3;1-1-4;1-1-5;1-1-6; 1-2-1;1-2-2;1-2-3;1-2-4;1-2-5;1-2-6; 2-1-1;2-1-2;2-1-3;2-1-4;2-1-5;2-1-6, azaz összesen 17 eset

4dobásból van vége a játéknak: 1-1-1-1;1-1-1-2;1-1-1-3;1-1-1-4;1-1-1-5;1-1-1-6, azaz összesen 6 eset

több változat nincs,mert 4pozitív szám összege legalább négy és 4 mezőre voltunk a céltól.

Amikor több,mint két dobás kell, azon esetek száma 17+6=23, az összes eseté pedig 41, tehát a keresett valószínűség 23/41.

Bogár Blanka 7.o.

[431] nadorp2008-12-20 10:22:54

Megjegyzés az A.465. számú feladat megoldásához ( másképp számolva)

Ha 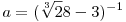a=(\root3\of28-3)^{-1},akkor

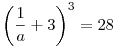\left(\frac1a+3\right)^3=28, azaz "a" gyöke az

x3-27x2-9x-1=0 egyenletnek. Ha ennek az egyenletnek a másik két gyöke b és c - melyek nyilván komplex számok és egymás konjugáltjai -, akkor a megoldásban közölt S összegre

S=an+bn+cn

A gyökök és együtthatók összefüggése alapján

a+b+c=27

a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=272-2.(-9)=747

Tekintsük ezek után az

xn+3=27.xn+2+9.xn+1+xn rekurziót a x0=3, x1=27, x2=747 kezdeti értékekkel. A rekurzió karakterisztikus egyenletének gyökei éppen a,b és c, tehát

xn=an+bn+cn

másrészt az xn sorozat elemei egész számok sőt egyszerű indukcióval adódik, hogy 6k+3 alakúak. Mivel abc=1, ezért

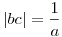
|bc|=\frac1a

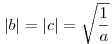|b|=|c|=\sqrt{\frac1a}, azaz

x_n=a^n+\frac2{{\sqrt a}^n}\cos n\phi alakú alkalmas \phi értékre. Innen a>27 miatt már látszik, hogy

xn-1<an<xn+1, azaz [an]=xn vagy [an]=xn-1, tehát 6k+2 vagy 6k+3 alakú

[430] nadorp2008-11-23 22:25:09

Most már látom mi tévesztett meg,elírtam. Helyesen:

Ha az eredeti állításs HAMIS lenne ...

Előzmény: [427] rizsesz, 2008-11-22 17:23:13
[429] Róbert Gida2008-11-23 03:52:10

??? A segédtétel megfordítása triviális. Amúgy több is igaz. Szép megoldás.

Előzmény: [427] rizsesz, 2008-11-22 17:23:13
[428] Valezius2008-11-22 17:26:47

Teljesen jó bizonyítás, gondold át újra :) Indirekt tegyük fel, hogy a keresett szám racionális, akkor a segédtétel miatt a 100. hatványösszeg is racionális. Ezzel megvan a kívánt ellentmondás.

Előzmény: [427] rizsesz, 2008-11-22 17:23:13
[427] rizsesz2008-11-22 17:23:13

Na, jól megfogalmaztam - szóval a segédtétel bizonyítása jó, de a végén pont a fordított állítást használod fel.

Előzmény: [426] rizsesz, 2008-11-22 17:22:28
[426] rizsesz2008-11-22 17:22:28

Nem jó a bizonyításod. A segédtételt legalábbis csak az egyik irányban bizonyítod be, viszont a megoldásod végén a másik irányt használod ki.

Előzmény: [425] nadorp, 2008-11-22 16:23:36
[425] nadorp2008-11-22 16:23:36

Az alábbi megoldás kicsit egyszerűbb a közöltnél és általánosabb is

B. 4109. Igazoljuk, hogy

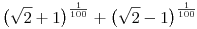
\big(\sqrt{2}+1\big)^{\frac{1}{100}}+ \big(\sqrt{2}-1\big)^{\frac{1}{100}}

irracionális szám.

Bebizonyítjuk a következő segédállítást:

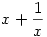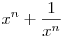Ha x+\frac1x racionális, akkor x^n+\frac1{x^n} is racionális minden pozitív egész n-re

Az állítás n=1 esetén nyilván igaz,n=2-re

x^2+\frac1{x^2}=\left(x+\frac1x\right)^2-2 miatt szintén teljesül.

Ha n>2, akkor indukcióval

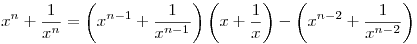
x^n+\frac1{x^n}=\left(x^{n-1}+\frac1{x^{n-1}}\right)\left(x+\frac1x\right)-\left(x^{n-2}+\frac1{x^{n-2}}\right)

miatt n-re is igaz a segédállítás.

Ha az eredeti feladat állítása igaz lenne, akkor a segédállításban x=(\sqrt2+1)^{\frac1{100}} és n=100 értékeket véve

(\sqrt2+1)+(\sqrt2-1)=2\sqrt2 is racionális lenne, ami ellentmondás

[424] KK072008-11-19 18:48:53

Azt szeretném megtudni hogy a a C951 -s feladatnál nem volt megadva hogy melyik saroktól számolom, és én azt küldtem be ha a jobbról számolom akkor 4, de ha balról akkor 12! Ez rossznak számít? Mert sztem akkor egyértelművé kellet volna tenni!

[423] Káli gúla2008-11-19 13:19:59

Igy lehetne "fejben" igazolni, hogy a szorzat valóban annyi, amennyi: 166*56=(100+66)*(100-66)=10000-662, és 662=62*112=30*121=3630, ezért a szorzat : 10000-3630=8590 (minden szám 12-es számrendszerben van írva).

[422] Káli gúla2008-11-19 10:35:12

Egyébként mindenféle polinomok nélkül a "kilences" próba azt adja a 166*56-8590-re (1+6+6=13, 5+6=11, 8+5+9+0=22), hogy 13*11-22 = 121 osztható (a-1)-gyel, tehát a=2, a=12 vagy a=122. Az alap páros, így 166*56 4-gyel osztható, ezért 8590 is, tehát a is 4-gyel osztható, vagyis a=12.

Előzmény: [421] Róbert Gida, 2008-11-19 02:01:49
[421] Róbert Gida2008-11-19 02:01:49

A komal.hu-n közölt C950. megoldása rossz, egy érettségin sem fogadnák el. Ha történetesen f(9)=0 volna akkor sem lenne megoldás, mivel a jegyek között szerepel a 9, így a számrendszer alapja nem lehet 9. f(12)=0, de ott sem nézte meg, hogy minden számjegy kisebb-e, mint 12.

[420] Róbert Gida2008-11-19 01:54:50

B.4413. négy potya pontért, a Maple szerint ugyanis:

factor(2*(a4+b4+c4+(-a-b-c)4)+8*a*b*c*(-a-b-c));

4*(a2+a*b+b2+a*c+b*c+c2)2

[419] KK072008-10-31 12:08:41

Helló mindenkinek! Nem tudná valaki fel tenni a szeptemberi megoldásokat, hogy össze vessem az enyéimmel! :) Előre is köszi, bár én nem tartozom a "nagyok közé" én még mindig csak a C kategóriával próbálkozom. Ezért elsősorban az érdekelne. :P Üdv: Kristóf

[418] Róbert Gida2008-10-27 14:27:39

Nem oldottam meg, de a konstans éles: http://www.mathlinks.ro/viewtopic.php?p=1187185#1187185

Előzmény: [417] janomo, 2008-10-27 08:47:45
[417] janomo2008-10-27 08:47:45

Hello!

Ha valaki tudja, örülnék, ha feltenné a tavalyi májusi A455 feladat megoldását.

N.J.

[416] lorantfy2008-09-17 10:24:15

Nagyon tetszik! Köszönöm, hogy feltetted!

Előzmény: [406] Káli gúla, 2008-06-16 17:00:58
[415] nadorp2008-09-10 15:26:51

A. 457.

Legyen p páratlan prímszám. Igazoljuk, hogy

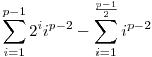
\sum_{i=1}^{p-1}2^ii^{p-2}-\sum_{i=1}^{\frac{p-1}2}i^{p-2}

osztható p-vel.

Azt bizonyítjuk be, hogy a mod p testben a fenti kifejezés 0, azaz a két összeg egyenlő.

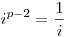Mivel 1\leqi\leqp-1 esetén i^{p-2}=\frac1i, ezért

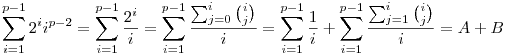
\sum_{i=1}^{p-1}2^ii^{p-2}=\sum_{i=1}^{p-1}\frac{2^i}i=\sum_{i=1}^{p-1}\frac{ \sum_{j=0}^i\binom{i}{j}}i=\sum_{i=1}^{p-1}\frac1i+\sum_{i=1}^{p-1}\frac{\sum_{j=1}^i\binom{i}{j}}i=A+B

Mivel 1\leqj\leqi esetén

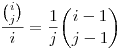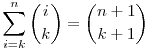\frac{\binom{i}{j}}i=\frac1j\binom{i-1}{j-1}, ezért felhasználva az ismert \sum_{i=k}^n\binom{i}{k}=\binom{n+1}{k+1} összefüggést

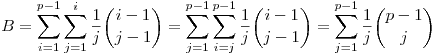
B=\sum_{i=1}^{p-1}\sum_{j=1}^i\frac1j\binom{i-1}{j-1}=\sum_{j=1}^{p-1}\sum_{i=j}^{p-1}\frac1j\binom{i-1}{j-1}=\sum_{j=1}^{p-1}\frac1j\binom{p-1}{j}

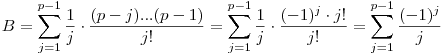B=\sum_{j=1}^{p-1}\frac1j\cdot\frac{(p-j)...(p-1)}{j!}=\sum_{j=1}^{p-1}\frac1j\cdot\frac{(-1)^j\cdot j!}{j!}=\sum_{j=1}^{p-1}\frac{(-1)^j}j Tehát

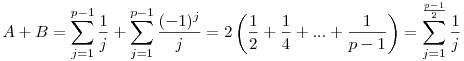
A+B=\sum_{j=1}^{p-1}\frac1j+\sum_{j=1}^{p-1}\frac{(-1)^j}j=2\left(\frac12+\frac14+...+\frac1{p-1}\right)=\sum_{j=1}^{\frac{p-1}2}\frac1j

és ezt kellett belátni

[414] Róbert Gida2008-06-19 11:50:41

Akkor szerinted 24 darab 5 pontos megoldás fog érkezni a feladatra? Kizárt. Egyébként nem kell hozzá semmilyen trükk. Angolul is fent vannak a feladatok a Kömalon, csak a feladat pontos szövegére rákeresve a harmadik találat, de az első is a Putnam feladatról szól, de az fizetős cikk.

"Sajnos manapság az Internet korában sokkal nehezebb olyan feladatot kitűzni, amit nem lehet a Google-lal megoldani."

Ezért kell eredeti feladatokat kitűzni...

Előzmény: [413] jenei.attila, 2008-06-19 09:40:37
[413] jenei.attila2008-06-19 09:40:37

Köszi, valószínűleg megtaláltam volna előbb-utóbb én is, de először magamtól akartam megoldani (így azért nem volt olyan könnyű, legalábbis nekem). Másrészt, még arra voltam kiváncsi, ki hogyan oldotta meg, mit gondol a feladatról. Sajnos manapság az Internet korában sokkal nehezebb olyan feladatot kitűzni, amit nem lehet a Google-lal megoldani. Végülis, szerintem egy verseny nem erről kell, hogy szóljon, de talán még a fórum sem. Szerintem előbb próbálja mindenki saját fejéből megoldani, mások megoldásához hozzászólni, megbeszélni a dolgokat. A Google keresőszavakat szerintem mindenki maga ki tudja találni.

Előzmény: [412] Róbert Gida, 2008-06-18 22:41:57
[412] Róbert Gida2008-06-18 22:41:57

1992-es Putnam verseny A6-os példája volt ez az A jelű feladat n=4-re, megoldása is fent van például D.J.Bernstein honlapján: http://www.math.niu.edu/ rusin/problems-math/bernstein92

De általánosított feladat megoldása is fent van, tetszőleges dimenzióra! Az eredmény az amit Káli gúla is írt:

http://www.mathematik.uni-bielefeld.de/ sillke/PUZZLES/ranpoint.txt

5 perc Google keresés volt az egész. Jelenleg mindössze a 4. találat egyébként a következő kulcsszavakkal találtam: sphere+convex hull+probability+n points containing the origin

Talán nem ezt a példát kellett volna feladni..... Így túl könnyű.

Előzmény: [411] jenei.attila, 2008-06-18 21:47:56
[411] jenei.attila2008-06-18 21:47:56

Nagyon szép gondolat. De ugye a "Tekintsük a pólusokhoz tartozó félgömbök közül azt, amelyik az illető pólust tartalmazza" mondatod helyesen "Tekintsük a pólusokhoz tartozó félgömbök közül azokat, amelyek az illető tartományt tartalmazzák"? Legalábbis számomra így érthető. A magasabb dimenzióra való általánosítás továbbra sem világos, de lehet,hogy csak a megfelelő fogalmakat kellene tisztázni (mint pl. a gömbfelszín két pontjához húzott sugarak által bezárt szög). Ezt az un-re vonatkozó rekurziót kicsit nehezen hoztam össze, csak utólag (a tn ismeretében) tudtam közvetlenül megmagyarázni, pedig így már nem is olyan nehéz. Egyébként biztos vagyok benne, hogy ez egy jól ismert kivesézett probléma (még nem néztem utána), és esetleg lehet rá valami geometriai valószínűséggel operáló megoldás (mint körvonalon 3 pont esete, amely nemrég egy B feladat volt). Mit tudtok erről?

Előzmény: [402] Káli gúla, 2008-06-13 16:12:29
[410] rizsesz2008-06-17 16:14:37

Az hogy akkor egy feladatra nem érkezett megoldás, az nem tudom, hogy miért nem jelentheti azt, hogy akkoriban a megoldók birtokában nem volt olyan tudásanyag, mint a mai versenyzőkében (és hogy miért kell egyből a lapot bántani megint - ráadásul elképzelésem sincsen, hogy a mai fejeddel, mert ha jól gondolom időközben elvégeztél valamilyen jópofa matek ttk szakot (az a sejtésem, hogy eltét) hogyan tudod megítélni, hogy a mai feladatok könnyebbek. Én egy középszerű dupla B díjazott vagyok, bár, főleg 12.-ben inkább a nehezebb példák mozgattak meg. Egyetem alatt már az A-k is sokkal barátságosabbak lettek.

Előzmény: [408] Róbert Gida, 2008-06-17 00:09:49
[409] Róbert Gida2008-06-17 00:14:25

Ez nem tudom, mire vonatkozik. Ha a monogramomra, akkor nem talált.

Előzmény: [405] rizsesz, 2008-06-15 15:45:53

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]