KöMaL Problems in Mathematics, September 2022
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2022. |
K. 729. What angle is enclosed by the hands of the tower hall clock 2022 minutes before it strikes midnight?
(Based on the idea of K.A. Kozma, Győr)
(5 pont)
solution (in Hungarian), statistics
K. 730. Eight chords are drawn in a circle, such that they have the largest possible number of intersections. Into how many regions will the eight chords divide the disc bounded by the circle?
(5 pont)
solution (in Hungarian), statistics
K. 731. A \(\displaystyle 4\times6\) rectangle is to be covered, without overlaps, with tiles congruent to the L-shape shown in the figure. The L-shaped tiles may be rotated or turned over as needed. Are there at least 36 different arrangements possible?
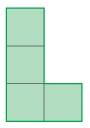
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on October 10, 2022. |
K/C. 732. Four mathematics teachers are all younger than 70 years, and the age of each of them is a prime number of years. How old is the youngest if their average age is 60 and all their ages are different?
(5 pont)
solution (in Hungarian), statistics
K/C. 733. What is the area of the smallest rectangle that has an inscribed parallelogram in which one angle is \(\displaystyle 60^{\circ}\), sides are 4 cm and 6 cm long, and two sides lie on two sides of the rectangle?
(5 pont)
 |
Problems with sign 'C'Deadline expired on October 10, 2022. |
C. 1728. Find the exact solutions of the equation
\(\displaystyle -\frac{1}{6}x+\frac{1}{2}=\{x\}. \)
(\(\displaystyle \{x\}\) denotes the fractional part of \(\displaystyle x\), that is, the difference between \(\displaystyle x\) and the greatest integer not greater than \(\displaystyle x\).)
(5 pont)
solution (in Hungarian), statistics
C. 1729. Semicircles \(\displaystyle k_1\) and \(\displaystyle k_2\), respectively, are drawn outside a square \(\displaystyle ABCD\), over the sides \(\displaystyle BC\) és \(\displaystyle CD\) as diameters. The midpoints of the semicircular arcs are \(\displaystyle E\) and \(\displaystyle F\), and the midpoints of line segments \(\displaystyle DE\) and \(\displaystyle AF\) are \(\displaystyle P\) and \(\displaystyle Q\), respectively. Show that \(\displaystyle P\) lies on diagonal \(\displaystyle AC\) and \(\displaystyle Q\) lies on diagonal \(\displaystyle BD\) of the square.
(5 pont)
solution (in Hungarian), statistics
C. 1730. Find all decimal numbers of the form \(\displaystyle \overline{0.abc}\) where \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) are digits, \(\displaystyle a\ne 0\), and \(\displaystyle \overline{0.abc}=\dfrac{a}{a+b+c}\).
(Croatian problem)
(5 pont)
solution (in Hungarian), statistics
C. 1731. The parallel sides of a trapezium \(\displaystyle ABCD\) are \(\displaystyle AB>CD\). The midline of the trapezium intersects diagonal \(\displaystyle AC\) at \(\displaystyle E\) and diagonal \(\displaystyle BD\) at \(\displaystyle F\). The length of line segment \(\displaystyle CD\) is the
\(\displaystyle a)\) arithmetic
\(\displaystyle b)\) geometric mean of line segments \(\displaystyle AB\) and \(\displaystyle EF\).
In which of the two cases will the ratio \(\displaystyle \dfrac{AB}{CD}\) have a larger value?
(5 pont)
solution (in Hungarian), statistics
C. 1732. Let \(\displaystyle U\) denote the set of prime numbers greater than \(\displaystyle 337\) but not greater than \(\displaystyle 733\). How many \(\displaystyle 4\)-element subset does \(\displaystyle U\) have that contain \(\displaystyle 467\) or \(\displaystyle 499\) as an element?
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 10, 2022. |
B. 5254. Prove that the difference of the squares of any two odd numbers not divisible by 3 is divisible by 24.
(Journal of Mathematics and Science Didactics, 1943)
(3 pont)
solution (in Hungarian), statistics
B. 5255. Vertex \(\displaystyle A\) of a triangle \(\displaystyle ABC\) is reflected about vertex \(\displaystyle B\), \(\displaystyle B\) is reflected about \(\displaystyle C\), and \(\displaystyle C\) is reflected about \(\displaystyle A\). The reflections are points \(\displaystyle C_1\), \(\displaystyle A_1\) and \(\displaystyle B_1\), respectively. Show that there exists a triangle with sides of lengths \(\displaystyle AA_1\), \(\displaystyle BB_1\) and \(\displaystyle CC_1\).
(3 pont)
solution (in Hungarian), statistics
B. 5256. In the lottery game, five numbers are drawn out of ninety every week. Andrew fills out a single lottery ticket with the same five numbers in each of the 52 weeks of the year. Belle uses a different scheme. She plays only once a year with 52 tickets simultaneously: she fills them out in pairwise different ways. Is it true that both of them have the same chance of having a ticket with five correct numbers?
(4 pont)
solution (in Hungarian), statistics
B. 5257. In an acute-angled triangle \(\displaystyle ABC\), the heights are \(\displaystyle AA_1\), \(\displaystyle BB_1\), \(\displaystyle CC_1\), and the midpoint of side \(\displaystyle AB\) is \(\displaystyle F\). A circle \(\displaystyle k\) passes through the points \(\displaystyle F\) and \(\displaystyle C_1\), and intersects the extensions of line segments \(\displaystyle A_1C_1\) and \(\displaystyle B_1C_1\) beyond \(\displaystyle C_1\) at points \(\displaystyle P\) and \(\displaystyle Q\), respectively. Prove that \(\displaystyle A_1P=B_1Q\).
(4 pont)
solution (in Hungarian), statistics
B. 5258. Is it true that every positive integer has a positive multiple in which the sum of the digits in decimal notation is at most 2022?
Proposed by Cs. Sándor, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5259. Solve the following simultaneous equations over the set of real numbers:
$$\begin{eqnarray*} x^2- 3y + 4 &=& z, \\ y^2 -3z + 4 &=& w,\\ z^2 - 3w +4 &=& x,\\ w^2 - 3x + 4 &=& y. \end{eqnarray*}$$Based on the idea of M. Bencze, Brassó
(4 pont)
solution (in Hungarian), statistics
B. 5260. \(\displaystyle G\) and \(\displaystyle H\) are points of chord \(\displaystyle AB\) of a circle \(\displaystyle k\) such that \(\displaystyle AG=GH=HB=1\). Let \(\displaystyle F\) denote the midpoint of one of the arcs \(\displaystyle AB\). The secants \(\displaystyle FH\) and \(\displaystyle FG\) intersect the circle again at points \(\displaystyle C\) and \(\displaystyle D\), respectively. Show that \(\displaystyle CD=BC^2\).
Proposed by Sz. Kocsis, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5261. Starting Player and Second Player are playing a game on the edges of a complete graph of 100 vertices. They take turns in colouring an edge of the graph that has not been coloured before. In each step, Starting Player colours his edge red, and Second Player colours his edge blue. The game terminates and Starting Player wins if there is a set of four vertices such that all the six connecting edges are red. The game terminates and Second Player wins if there is a set of four vertices such that all the six connecting edges are blue. The game terminates with a draw if there is no such set of four vertices but there remain no further vertices to colour. Who has a winning strategy?
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 10, 2022. |
A. 830. For \(\displaystyle H\subset \mathbb{Z}\) and \(\displaystyle n\in \mathbb{Z}\), let \(\displaystyle h_n\) denote the number of finite subsets of \(\displaystyle H\) in which the sum of the elements is \(\displaystyle n\). Does there exist \(\displaystyle H\subset \mathbb{Z}\), for which \(\displaystyle 0\notin H\), and \(\displaystyle h_n\) is a (finite) even number for every \(\displaystyle n\in \mathbb{Z}\)? (The sum of the elements of the empty set is 0.)
Submitted by Csongor Beke, Cambridge
(7 pont)
A. 831. In triangle \(\displaystyle ABC\) let \(\displaystyle F\) denote the midpoint of side \(\displaystyle BC\). Let the circle passing through point \(\displaystyle A\) and tangent to side \(\displaystyle BC\) at point \(\displaystyle F\) intersect sides \(\displaystyle AB\) and \(\displaystyle AC\) at points \(\displaystyle M\) and \(\displaystyle N\), respectively. Let line segments \(\displaystyle CM\) and \(\displaystyle BN\) intersect in point \(\displaystyle X\). Let \(\displaystyle P\) be the second point of intersection of the circumcircles of triangles \(\displaystyle BMX\) and \(\displaystyle CNX\). Prove that points \(\displaystyle A\), \(\displaystyle F\) and \(\displaystyle P\) are collinear.
(7 pont)
A. 832. Let us assume that the number of offsprings for every man can be \(\displaystyle 0, 1,\dots\) or \(\displaystyle n\) with probabilities \(\displaystyle p_0,p_1,\dots,p_n\) independently from each other, where \(\displaystyle p_0+p_1+\dots+p_n=1\) and \(\displaystyle p_n \ne 0\). (This is the so called Galton–Watson process.)
Which positive integer \(\displaystyle n\) and probabilities \(\displaystyle p_0,p_1,\dots,p_n\) will maximize the probability that the offsprings of a given man go extinct in exactly the tenth generation?
(7 pont)
Upload your solutions above.
