KöMaL Problems in Mathematics, February 2023
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 10, 2023. |
K. 754. Matt and Seb are playing tic-tac-toe. When Seb wins, he will get 3 candies from Matt. When Matt wins, he will get 2 candies from Seb. (There is no draw.) After 30 games, Seb had the same number of candies as initially. How many games did Seb win?
(5 pont)
solution (in Hungarian), statistics
K. 755. What is the maximum possible number of sides that a convex polygon may have if it has exactly 3 obtuse angles? Give an example of such a polygon.
(5 pont)
solution (in Hungarian), statistics
K. 756. A shop sells wooden cubes in two sizes: cubes of edge 1 cm and those with edges of 2 cm. The surfaces of the cubes are painted. In the case of the smaller cubes the paint represents 60% of the material costs, while the rest is the price of the wood. Both kinds of cube are made of the same type of wood and they are coated with a thin layer of paint with the same thickness. Labour costs are the same for each cube, independent of the size.
Considering all costs, it costs the shop 830 forints (HUF, Hungarian currency) to manufacture 10 small cubes and 5 large ones. 5 small cubes and 15 large ones cost 1490 forints to manufacture. What is the labour cost of one cube?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on March 10, 2023. |
K/C. 757. Kate is planning to cut a \(\displaystyle 4\times4\) sheet of squared paper into pieces with scissors, cutting along grid lines only. Show that she can make exactly 11 different kinds of puzzle that is symmetrical in all four symmetry axes of the original square sheet. The diagram shows a possible puzzle.
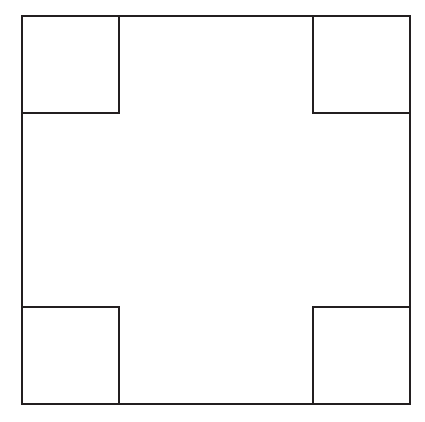
(5 pont)
solution (in Hungarian), statistics
K/C. 758. A sail is shaped like a right angled triangle and it has the red symbol of the boat class at a height such that \(\displaystyle MA + AC = CB + BM\) (see the figure). If \(\displaystyle BM = 7\) m and \(\displaystyle CB = 5\) m, what is the height of the peak of the sail above the red mark?
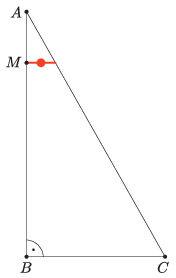
(5 pont)
 |
Problems with sign 'C'Deadline expired on March 10, 2023. |
C. 1753. A long strip of paper is divided into squares. The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 are written in the first ten squares, then the same numbers are written in the next ten squares, too, and so on. There are exactly 2030 squares numbered in this way. A token is placed in square \(\displaystyle 1\). In each move, the token is moved as many squares ahead as the number written in the square it is standing on. What is the number in the square where the token is when its next move would get out off the paper strip of length \(\displaystyle 2030\)?
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1754. Squares \(\displaystyle ABCD, BEFC\) and \(\displaystyle EGHF\) are drawn next to each other in a plane. The foot of the perpendicular drawn from \(\displaystyle B\) to \(\displaystyle DE\) is \(\displaystyle K\). Show that the points \(\displaystyle A\), \(\displaystyle K\), \(\displaystyle H\) are collinear.
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1755. What integers \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) satisfy the equality \(\displaystyle a^2+b^2-8c=6\)?
(Canadian problem)
(5 pont)
solution (in Hungarian), statistics
C. 1756. Solve the equation
\(\displaystyle 4\cdot \cos\big(\pi\cdot \sin {(\pi \cdot x)}\big)=-5x^2+15x-\frac{61}{4} \)
over the set of real numbers.
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1757. Johnny got a robot for Christmas, and he is trying it on a square carpet. The length of the sides of the square is \(\displaystyle 4\) metres, and its vertices are \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) and \(\displaystyle D\), in this order. Let \(\displaystyle P\) denote the interior point of square \(\displaystyle ABCD\) which is exactly \(\displaystyle 1\) metre away from both of sides \(\displaystyle AB\) and \(\displaystyle BC\). The robot is initially standing at point \(\displaystyle P\), and starts to move in a random direction. When it has covered \(\displaystyle 2\) metres, it will stop. What is the probability that the robot will get off the carpet?
Proposed by K.\(\displaystyle \,\)A. Kozma, Győr
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 10, 2023. |
B. 5294. Two altitudes of an acute-angled triangle \(\displaystyle ABC\) are \(\displaystyle AT_A\) and \(\displaystyle BT_B\). The midpoint of \(\displaystyle AB\) is \(\displaystyle F\), and the midpoint of \(\displaystyle T_AT_B\) is \(\displaystyle G\). Prove that \(\displaystyle FG\) is perpendicular to \(\displaystyle T_AT_B\).
Proposed by V. Vígh, Sándorfalva
(3 pont)
solution (in Hungarian), statistics
B. 5295. Find the largest integer \(\displaystyle k\) for which \(\displaystyle 1722\) divided by \(\displaystyle k\) leaves a remainder of \(\displaystyle 2m\) and \(\displaystyle 2179\) divided by \(\displaystyle k\) leaves a remainder of \(\displaystyle 3m\) (for some appropriate natural number \(\displaystyle 0 \le m < k/3\)).
Proposed by K.\(\displaystyle \,\)A. Kozma, Győr
(3 pont)
solution (in Hungarian), statistics
B. 5296. A rook is moving from the bottom left corner of a \(\displaystyle 8\times 8\) chessboard to the top right corner. It starts by moving to the right, then up, and so on, right and up alternatingly. How many different sequences of moves are there?
Proposed by B. Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5297. In a triangle \(\displaystyle ABC\), \(\displaystyle \angle BAC =2\angle CBA\). Let \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) denote interior points of sides \(\displaystyle CA\), \(\displaystyle AB\) and \(\displaystyle BC\), respectively, such that triangle \(\displaystyle A'B'C'\) is similar to triangle \(\displaystyle ABC\). Show that the angle bisectors of angles \(\displaystyle BAC\) and \(\displaystyle B'A'C'\) intersect each other on the line segment \(\displaystyle B'C'\).
Proposed by G. Kós, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5298. Solve the following system of equations over the set of real numbers:
$$\begin{align*} y+yx^2-2x & =0,\\ z+zy^2-2y & =0,\\ x+xz^2-2z & =0. \end{align*}$$American problem
(5 pont)
solution (in Hungarian), statistics
B. 5299. There is a flea sitting at each of points \(\displaystyle 1,2,3\) of the number line. If one flea is at point \(\displaystyle a\) and another is at point \(\displaystyle b\), then the flea at \(\displaystyle a\) may jump to the point \(\displaystyle 2b-a\). Is it possible for the fleas to end up at points \(\displaystyle 2^{100},3^{100},2^{100}+3^{100}\) with a finite sequence of such steps?
Proposed by P.\(\displaystyle \,\)P. Pach, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5300. Let \(\displaystyle T\) be a regular tetrahedron of unit edge. Inscribe a cube in \(\displaystyle T\) such that exactly two vertices of the cube lie on each face of \(\displaystyle T\), as shown in the figure (the dashed lines are parallel to the appropriate edges of the tetrahedron). What is the volume of the cube?
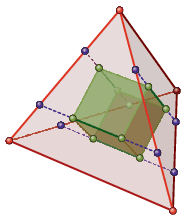
Proposed by V. Vígh, Sándorfalva
(5 pont)
solution (in Hungarian), statistics
B. 5301. Given that the sum of the reciprocals of ten distinct positive integers is 1, prove that each of them is smaller than \(\displaystyle 10^{1000}\).
Proposed by V. Vígh, Sándorfalva
(6 pont)
 |
Problems with sign 'A'Deadline expired on March 10, 2023. |
A. 845. The incircle of triangle \(\displaystyle ABC\) is tangent to sides \(\displaystyle BC\), \(\displaystyle AC\), and \(\displaystyle AB\) at points \(\displaystyle D\), \(\displaystyle E\), and \(\displaystyle F\), respectively. Let \(\displaystyle A'\) denote the point of the incircle for which circle \(\displaystyle (A'BC)\) is tangent to the incircle. Define points \(\displaystyle B'\) and \(\displaystyle C'\) similarly. Prove that lines \(\displaystyle A'D\), \(\displaystyle B'E\) and \(\displaystyle C'F\) are concurrent.
Proposed by Áron Bán-Szabó, Budapest
(7 pont)
A. 846. Let \(\displaystyle n\) be a positive integer and let vectors \(\displaystyle v_1,v_2,\ldots,v_n\) be given in the plain. A flea originally sitting in the origin moves according to the following rule: in the \(\displaystyle i^{\text{th}}\) minute (for \(\displaystyle i=1,2,\ldots,n\)) it will stay where it is with probability \(\displaystyle 1/2\), moves with vector \(\displaystyle v_i\) with probability \(\displaystyle 1/4\), and moves with vector \(\displaystyle -v_i\) with probability \(\displaystyle 1/4\). Prove that after the \(\displaystyle n^{\text{th}}\) minute there exists no point which is occupied by the flea with greater probability than the origin.
Proposed by Péter Pál Pach, Budapest
(7 pont)
A. 847. Let \(\displaystyle A\) be a given finite set with some of its subsets called pretty. Let a subset be called small, if it's a subset of a pretty set. Let a subset be called big, if it has a pretty subset. (A set can be small and big simultaneously, and a set can be neither small nor big.) Let \(\displaystyle a\) denote the number of elements of \(\displaystyle A\), and let \(\displaystyle p\), \(\displaystyle s\) and \(\displaystyle b\) denote the number of pretty, small and big sets, respectively. Prove that \(\displaystyle 2^a\cdot p\le s \cdot b\).
Proposed by András Imolay, Budapest
(7 pont)
Upload your solutions above.
