KöMaL Problems in Mathematics, January 2021
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 15, 2021. |
K. 679. Pete was three years old when he got a set of six rectangular building blocks. The dimensions of the blocks are \(\displaystyle 1~ \mathrm{dm} \times 1~ \mathrm{dm} \times 2~ \mathrm{dm}\). The dimensions of the interior of the box for storing the blocks are \(\displaystyle 3~ \mathrm{dm} \times 2~ \mathrm{dm} \times 2~ \mathrm{dm}\) and each face is different in colour. In how many different arrangements may Pete place the blocks in the box if the blocks are identical in colour and cannot be distinguished? (It is not allowed for any block to stick out of the box).
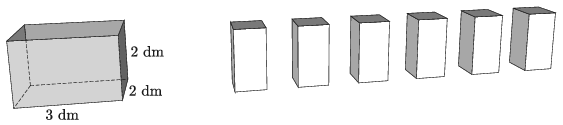
(6 pont)
solution (in Hungarian), statistics
K. 680. Four faces of a cube are coloured red, and then the cube is cut into 125 identical small cubes. What may be the number of small cubes with no red face?
(6 pont)
solution (in Hungarian), statistics
K. 681. How many triangles are there in which the sides have integer lengths in centimetres, and the longest side is 2021 cm long? (There may be more than one side of this length.)
(6 pont)
solution (in Hungarian), statistics
K. 682. There is a sufficient number of copies of three different cards, with one digit on each. All possible four-digit positive numbers are formed out of the cards. The sum of these numbers is \(\displaystyle 689\,931\). What are the three digits on the cards?
(6 pont)
solution (in Hungarian), statistics
K. 683. A heptagon \(\displaystyle ABCDEFG\) is inscribed in a circle. The sum of angles \(\displaystyle \angle ABC\), \(\displaystyle \angle CDE\) and \(\displaystyle \angle EFG\) is greatrer than \(\displaystyle 450^{\circ}\). Show that the centre of the circumscribed circle cannot lie either inside the heptagon or on its boundary.
(The University of Stirling, school mathematics competition, 1983)
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 15, 2021. |
C. 1644. We have made a \(\displaystyle 10 \mathrm{cm} \times 30 \mathrm{cm}\) rectangular tin of shortbread. It has a delicious crispy edge. We want to divide the bread into pieces by using cuts running all the way parallel to the edges of the tin. How many pieces may we obtain if we would like each piece to have the same length of crispy edge?
(5 pont)
solution (in Hungarian), statistics
C. 1645. In an acute-angled triangle, the sides are \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), and \(\displaystyle m_b\) is the height drawn to side \(\displaystyle b\). The lengths of \(\displaystyle m_b\), \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), in this order, are consecutive positive integers. What is the area of the triangle?
Proposed by Zs. M. Tatár, Esztergom
(5 pont)
solution (in Hungarian), statistics
C. 1646. Find the integer solutions of the equation \(\displaystyle {(xy-1)}^2 = {(x + 1)}^2 + {(y + 1)}^2\).
Proposed by M. Szalai, Szeged
(5 pont)
solution (in Hungarian), statistics
C. 1647. The medians drawn to the legs of an isosceles triangle are perpendicular to each other. Let \(\displaystyle r\) and \(\displaystyle R\) denote the inradius and circumradius, respectively. Find the exact value of the ratio \(\displaystyle \frac{r}{R}\).
(5 pont)
solution (in Hungarian), statistics
C. 1648. King Arthur and Sir Lancelot are running a horse race. Sir Lancelot says, ``Since Your Majesty's speed is only \(\displaystyle \frac{2}{3}\) of mine, I will give Your Majesty a handicap of \(\displaystyle 100\) metres, and then I would catch up within the length of the race track. Alternatively, if Your Majesty reduced speed by \(\displaystyle 2 \frac{\mathrm{m}}{\mathrm{s}}\) and I reduced mine by \(\displaystyle 5 \frac{\mathrm{m}}{\mathrm{s}}\), but I gave Your Majesty a \(\displaystyle 50\) metre handicap only, I would also be able to catch up within the length of the track. The sum of the two time intervals required to catch up is exactly \(\displaystyle 75\) seconds.'' Determine the speeds of King Arthur and of Sir Lancelot.
(5 pont)
solution (in Hungarian), statistics
C. 1649. The diagonals of a cyclic quadrilateral intersect each other at right angles at point \(\displaystyle M\). The diagonals divide the quadrilateral into triangles. Prove that the altitude of any triangle drawn from point \(\displaystyle M\) is collinear with the median drawn from point \(\displaystyle M\) in the opposite triangle.
(5 pont)
solution (in Hungarian), statistics
C. 1650. Prove the inequality
\(\displaystyle \log_{ab}c\le \frac{\log_ac + \log_bc}{4} \)
for \(\displaystyle a, b, c>1\).
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 15, 2021. |
B. 5142. In a football championship, there are four teams in a group. Within the group, each team plays every other team once. The teams receive 3 points for winning, 1 point for a draw and 0 points for losing a game. The two teams scoring the highest qualify for the semi-finals, and the other two teams are eliminated. In the case of equal scores, the qualification is decided by chance. Determine those values of the number \(\displaystyle p\) for which it may happen that a qualifying team and an eliminated team both have \(\displaystyle p\) points.
(3 pont)
solution (in Hungarian), statistics
B. 5143. Find the real solutions of the equation \(\displaystyle 16x^2+9x+117=24x\sqrt{x+13}\,\).
Proposed by S. Róka, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 5144. The area of a convex quadrilateral \(\displaystyle ABCD\) is \(\displaystyle t\), and an interior point is \(\displaystyle O\). Show that
\(\displaystyle 2t\le OA^2+OB^2+OC^2+OD^2. \)
When will equality occur?
(3 pont)
solution (in Hungarian), statistics
B. 5145. Show that there are \(\displaystyle \binom{n+1}{2k+1}\) different strings of zeros and ones of length \(\displaystyle n\) in which it occurs exactly \(\displaystyle k\) times that a \(\displaystyle 0\) is followed by a \(\displaystyle 1\).
(Problem from a qualifying competition in England for the Olympiad)
(4 pont)
solution (in Hungarian), statistics
B. 5146. \(\displaystyle T\) is a cuboid of unit volume, and \(\displaystyle M\) is a point in its interior. Point \(\displaystyle M\) is reflected in the planes of the faces. Let \(\displaystyle D\) be the convex hull of the \(\displaystyle 6\) images obtained. Determine the volume of the solid \(\displaystyle T\cap D\).
(5 pont)
solution (in Hungarian), statistics
B. 5147. Let \(\displaystyle k>1\) be a positive integer. Is there
\(\displaystyle a)\) a finite subset (of any size)
\(\displaystyle b)\) an infinite subset
of the set of positive integers in which the greatest common divisor of any \(\displaystyle k\) elements is greater than 1 but the greatest common divisor of any \(\displaystyle k+1\) elements is equal to 1?
Proposed by G. Mészáros, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5148. A triangle \(\displaystyle ABC\) is right angled at \(\displaystyle C\). The inscribed circle touches the leg \(\displaystyle BC\) at point \(\displaystyle D\), and the leg \(\displaystyle AC\) at point \(\displaystyle E\). The escribed circle of side \(\displaystyle BC\) touches line segment \(\displaystyle BC\) at point \(\displaystyle G\); and the escribed circle of side \(\displaystyle AC\) touches line segment \(\displaystyle AC\) at point \(\displaystyle H\). The intersection of line segments \(\displaystyle DH\) and \(\displaystyle EG\) is \(\displaystyle M\). Show that the other intersection of the circumscribed circles of triangles \(\displaystyle DGM\) and \(\displaystyle EHM\) lies on the inscribed circle.
(6 pont)
solution (in Hungarian), statistics
B. 5149. In how many different ways is it possible to fill in a \(\displaystyle 6\times 6\) table with the numbers \(\displaystyle 1,2,\dots,36\) so that however 6 fields are selected, all lying in different rows and in different columns, the sum of the numbers in 6 such fields should always be the same?
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 15, 2021. |
A. 791. A lightbulb is given that emits red, green or blue light and an infinite set \(\displaystyle S\) of switches, each with three positions labeled red, green and blue. We know the following:
\(\displaystyle i)\) For every combination of the switches the lighbulb emits a given color.
\(\displaystyle ii)\) If all switches are in a position with a given color, the lightbulb emits the same color.
\(\displaystyle iii)\) If there are two combinations of the switches where each switch is in a different position, the lightbulb emits a different color for the two combinations.
We create the following set \(\displaystyle U\) containing some of the subsets of \(\displaystyle S\): for each combination of the switches let us observe the color of the lightbulb, and put the set of those switches in \(\displaystyle U\) which are in the same position as the color of the lightbulb.
Prove that \(\displaystyle U\) is an ultrafilter on \(\displaystyle S\).
(\(\displaystyle U\) is an ultrafilter on \(\displaystyle S\) if it satisfies the following:
\(\displaystyle a)\) The empty set is not in \(\displaystyle U\).
\(\displaystyle b)\) If two sets are in \(\displaystyle U\), their intersection is also in \(\displaystyle U\).
\(\displaystyle c)\) If a set is in \(\displaystyle U\), every subset of \(\displaystyle S\) containing it are also in \(\displaystyle U\).
\(\displaystyle d)\) Considering a set and its complement in \(\displaystyle S\), exactly one of these sets is contained in \(\displaystyle U\).)
See also problem N.\(\displaystyle \,\)35. from the May issue of 1994 (in Hungarian).
(7 pont)
A. 792. Let \(\displaystyle p\ge 3\) be a prime number and \(\displaystyle 0\le r\le p-3\). Let \(\displaystyle x_1, x_2, \ldots, x_{p-1+r}\) be integer numbers satisfying \(\displaystyle \sum_{j=1}^{p-1+r}x_j^k\equiv r~ \textrm{(mod}\ p\textrm{)}\) for all \(\displaystyle 1\le k\le p-2\).
What are the possible remainders of numbers \(\displaystyle x_1,x_2,\ldots,x_{p-1+r}\) modulo \(\displaystyle p\)?
Submitted by Dávid Matolcsi, Budapest
(7 pont)
Upload your solutions above.
