| [110] lorantfy | 2005-12-20 23:58:51 |
 Szia Mate!
Szép a megoldás! A deriválást különben a faktosok tanulják a középiskolában, tehát ilyen szinten azért lehet alkalmazni. A deriválós megoldásból is ez a numerikus eredmény adódik, csak a végén a nagy kapkodásban a g mértékegységét nem vettem figyelembe. Hogy a deriválás áttekinthetőbb legyen az elején beírtam a numerikus értékeket, emiatt a g-t is cm/s2-ben kellett volna behelyettesíteni.
Kíváncsi vagyok, hány jó megoldás érkezett erre a feladatra!
Hogy lehet a szöveg közé ábrákat tenni?
|
| Előzmény: [109] Mate, 2005-12-20 18:54:15 |
|
| [109] Mate | 2005-12-20 18:54:15 |
 A deriválós megoldást át kellene nézni, ugyanezt az eredményt kellene kapnunk.
|
|
| [108] Mate | 2005-12-20 18:50:12 |
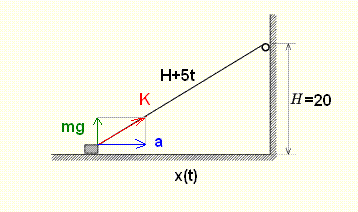
 A KöMaL középiskolásoknak szóló lap, s mint ilyen, minden feladat megoldható tisztán középiskolai ismeretekkel. Ha én most középiskolás lennék, a következőképpen oldanám meg deriválás nélkül ezt a példát:
A test vízszintesen v sebességgel mozog, s ennek a sebességnek a kötél irányú komponense éppen v0. Így
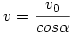
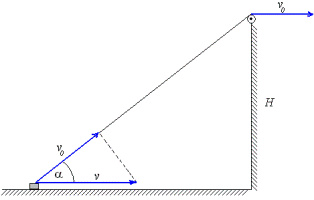
Az elválás pillanatában az asztal által kifejtett kényszererő (és így a súrlódási erő is) zérussá válik, ezért a test mozgásegyenletei:
Fsin -mg=0 -mg=0
Fcos =ma =ma
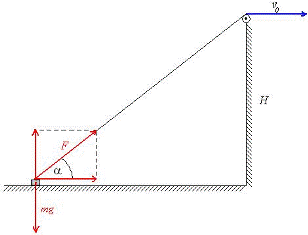
A test körmozgást végez a P pont körül, ezért a fenti mozgásegyenletbeli "a" gyorsulás előáll a centripetális és az érintőleges gyorsulás vektori összegeként, amint az az ábrán is látszik.
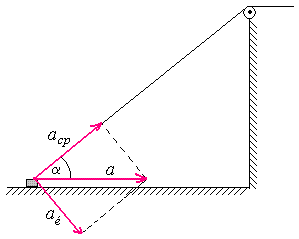
A centripetális gyorsulás 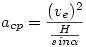 , ahol ve=vsin , ahol ve=vsin =v0tg =v0tg az érintőleges sebesség. Amint az az ábrából kitűnik, az érintőleges sebesség. Amint az az ábrából kitűnik,
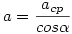
, vagyis
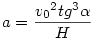
A mozgásegyenletekből az elváláskor a gyorsulásra 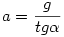 adódik, így az elválás szögére kapjuk: adódik, így az elválás szögére kapjuk:

, ekkor pedig a test faltól való távolsága:
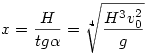
Numerikusan x 3,8 cm. 3,8 cm.
|
|
|
| [106] lorantfy | 2005-12-20 11:12:13 |
 Szia Iván!
Ahhoz, hogy a kötél irányú 5 m/s sebességet tartani tudja, a testnek a vizszintes síkon gyorsulva kell mozognia. Ez sajnos nem egyenletesen gyorsuló mozgás. A gyorsuláshoz szükséges erőt a kötélerő vizszintes kompononse biztosítja. Amikor a kötélerő függőleges komponense eléri a súlyerő nagyságát a test felemelkedik. Ebben a pillanatban nincs súrlódás, mert a nyomóerő nulla.
Arra gondoltam, hogy indítsuk a testet a sarokból és így keressük meg a feltételnek megfelelő pontot. Legyen a derékszögű csúcstól mért távolság x(t). Az átfogó c=20+5t.
x2(t)=(20+5t)2-202=25t2+200t

A sebesség x(t) első deriváltja t szerint:
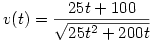
A gyorsulás meg a második derivált:
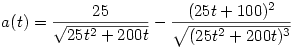
(25t+100)2=625t2+5000t+10000=25x2+10000
Így a(t) kifejezhető x(t)-vel. Röviden x-et írok:
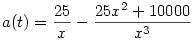
A háromszögek hasonlóságából látszik, hogy  Vegyük g-t 10 m/s2-nek és mivel fordítva játszuk a folyamatot bejön egy negatív előjel is: Vegyük g-t 10 m/s2-nek és mivel fordítva játszuk a folyamatot bejön egy negatív előjel is:
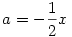 tehát az alábbi egyenletet kell megoldanunk: tehát az alábbi egyenletet kell megoldanunk:

Átszorozva 2x3-el: x4=20000, amiből x=3,45 cm adódik. Lehet, hogy hibás a megoldás. Nézzétek át, mert nagy kapkodásban kellett beírnom!
|
 |
| Előzmény: [105] Iván88, 2005-12-17 19:10:03 |
|
| [105] Iván88 | 2005-12-17 19:10:03 |
 Sziasztok! A P.3830-as feledatra nem tud valaki valami okosat, mert a suliban még a fizikatanáromnak sem volt eredményre vezető ötlete.
|
|
| [104] jenei.attila | 2005-12-15 21:23:53 |
 Kösz szépen, ez nagyon szép megoldás. Én egész másképp álltam neki (sokkal körülményesebben), azért nagy vonalakban leírom:
Teljes indukcióval bizonyítsunk, azaz tegyük fel, hogy a feltételeknek megfelelő n-1 darab x és y számokra teljesül az egyenlőtlenség. Ezután rögzített n-1 db. x,y-ra keressük xn,yn-et, amelyre xn-yn minimális. Ha így sikerül bebizonyítani az egyenlőtlenséget, nyilván bármely a feltételeknek megfelelő xn,yn-re is igaz lesz. A szóbanforgó minimumot könnyű meghatározni pl. grafikusan, ha a derékszögű koordinátarendszerben felrajzoljuk az y=mn-1x egyenest (ahol 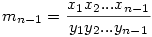 ). A szóba jöhető (xn,yn) pontok ezen egyenes, az x tengely, az x=xn-1 és y=yn-1 egyenesek által határolt trapézban (vagy háromszögben) helyezkednek el. Itt két esetet kell megkülönböztetnünk: ). A szóba jöhető (xn,yn) pontok ezen egyenes, az x tengely, az x=xn-1 és y=yn-1 egyenesek által határolt trapézban (vagy háromszögben) helyezkednek el. Itt két esetet kell megkülönböztetnünk:
1.) yn-1 mn-1xn-1 mn-1xn-1
Ekkor xn-yn minimális, ha 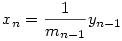 , és yn=yn-1. Az n-1 darab x,y-ra vonatkozó szumma egyenlőtlenséget erősítjük azáltal, hogy valamely xi helyett nála kisebb, a feltételeknek eleget tevő xi*-ot keresünk. Legyen i olyan 1 és n-1 közötti index, amelyre xi , és yn=yn-1. Az n-1 darab x,y-ra vonatkozó szumma egyenlőtlenséget erősítjük azáltal, hogy valamely xi helyett nála kisebb, a feltételeknek eleget tevő xi*-ot keresünk. Legyen i olyan 1 és n-1 közötti index, amelyre xi yi, de minden i-nél nagyobb és n-1 -nél kisebb-egyenlő j indexre xj<yj, és legyen yi, de minden i-nél nagyobb és n-1 -nél kisebb-egyenlő j indexre xj<yj, és legyen  . Ekkor xi helyett xi*-ot írva a szorzat feltétel teljesül, és ha xi* . Ekkor xi helyett xi*-ot írva a szorzat feltétel teljesül, és ha xi* xi-1, akkor az n-1 -ig terjedő szummában is az indukciós feltevés szerint írható xi helyett xi*. Ha xi*<xi-1, akkor az x-eket újra rendezve a szorzat feltétel méginkább teljesül (a baloldal nő), vagyis ekkor is fennáll a szumma egyenlőtlenség. xi-1, akkor az n-1 -ig terjedő szummában is az indukciós feltevés szerint írható xi helyett xi*. Ha xi*<xi-1, akkor az x-eket újra rendezve a szorzat feltétel méginkább teljesül (a baloldal nő), vagyis ekkor is fennáll a szumma egyenlőtlenség.
Könnyű bebizonyítani a
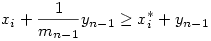
egyenlőtlenséget. Ezt, és az n-1 tagra vonatkozó szumma egyenlőtlenséget (amelyben xi helyett xi* szerpel) összeadva, kapjuk azt az n tagra vonatkozó szumma egyenlőtlenséget, amelyben  , vagyis xn-yn minimális rögzített n-1 darab x és y mellett. , vagyis xn-yn minimális rögzített n-1 darab x és y mellett.
2.) A második esetben amikor yn-1>mn-1xn-1,xn-yn akkor minimális, ha xn=xn-1 és yn=mn-1xn-1. Ilyenkor hasonlóan yi helyett nála nagyobb, a szorzat feltételt teljesítő yi*-ot lehet választani, de ha ez túl nagy lesz, az y-onok nem rendezhető újra az x-ekhez hasonlóan (itt akadtam el).
|
| Előzmény: [103] Ali, 2005-12-15 16:13:35 |
|
| [103] Ali | 2005-12-15 16:13:35 |
 A feladat azt állítja, hogy ha az x1 x2 x2 ... ... xn>0 és az y1 xn>0 és az y1 y2 y2 ... ... yn>0 számokra minden 0<k yn>0 számokra minden 0<k n esetén teljesül, hogy n esetén teljesül, hogy

akkor
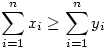
is teljesül.
Szorozzuk be xi- és yi számokat egy pozitív C konstanssal úgy, hogy mindegyikük 1-nél nagyobb legyen. Ekkor az eredeti feladattal ekvivalens feladathoz jutunk.
Legyen ai:=ln xi és bi:=ln yi. ekkor az ai és bi számokra is teljesül, hogy a1 a2 a2 ... ... an>0 és b1 an>0 és b1 b2 b2 ... ... bn>0. bn>0.
Továbbá a feltétel szerint minden 0<k n esetén teljesül, hogy n esetén teljesül, hogy
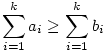
Könnyen igazolható hogy ea-eb (a-b)eb, akármilyen is legyen a és b viszonya. Ez következik pl. abból, hogy az ex függyvény görbéjének két pontját összekötő egyenes meredeksége a pontokbeli érintők meredekségei között van. (a-b)eb, akármilyen is legyen a és b viszonya. Ez következik pl. abból, hogy az ex függyvény görbéjének két pontját összekötő egyenes meredeksége a pontokbeli érintők meredekségei között van.
Azt kell igazolnunk, hogy

vagy másképpen
(ea1-eb1)+(ea2-eb2)+...+(ean-ebn) 0 0
Az eddigiek alapján
(ea1-eb1)+(ea2-eb2)+...+(ean-ebn) (a1-b1)eb1+(a2-b2)eb2+...(an-bn)ebn (a1-b1)eb1+(a2-b2)eb2+...(an-bn)ebn
A jobb oldalt nem növeljük, ha eb1 helyére eb2 -t írunk, mivel a1 b1 és b1 b1 és b1 b2 , kapjuk, hogy b2 , kapjuk, hogy
(ea1-eb1)+(ea2-eb2)+...+(ean-ebn) (a1-b1)eb1+(a2-b2)eb2+...+(an-bn)ebn (a1-b1)eb1+(a2-b2)eb2+...+(an-bn)ebn (a1+a2-b1-b2)eb2+(a3-b3)eb3+...+(an-bn)ebn (a1+a2-b1-b2)eb2+(a3-b3)eb3+...+(an-bn)ebn
Hasonlóan, mivel a1+a2 b1+b2 és b2 b1+b2 és b2 b3 kapjuk, hogy b3 kapjuk, hogy
(a1+a2-b1-b2)eb2+(a3-b3)eb3+...+(an-bn)ebn (a1+a2+a3-b1-b2-b3)eb3+(a4-b4)eb4+...+(an-bn)ebn (a1+a2+a3-b1-b2-b3)eb3+(a4-b4)eb4+...+(an-bn)ebn
és így tovább. Végül kapjuk, hogy
(ea1-eb1)+(ea2-eb2)+...+(ean-ebn) (a1+a2+...+an-b1-b2-...-bn)ebn (a1+a2+...+an-b1-b2-...-bn)ebn 0 0
amit bizonyítani akartunk.
|
| Előzmény: [102] jenei.attila, 2005-12-14 22:30:10 |
|
|
| [101] jenei.attila | 2005-12-13 13:32:53 |
 Oldjuk meg az A.374 -es feladatot. Elég sokat foglalkoztam vele,és majdnem be is bizonyítottam, de egy apró részleten ne jutok túl. Más fajta megoldás is érdekelne, illetve szívesen venném, ha az én próbálkozásomat segítenétek tovább vinni. Ha nem írtok megoldást, beírom hogy eddig mire jutottam. Addig is jó munkát.
|
|
| [100] lorantfy | 2005-11-20 16:03:39 |
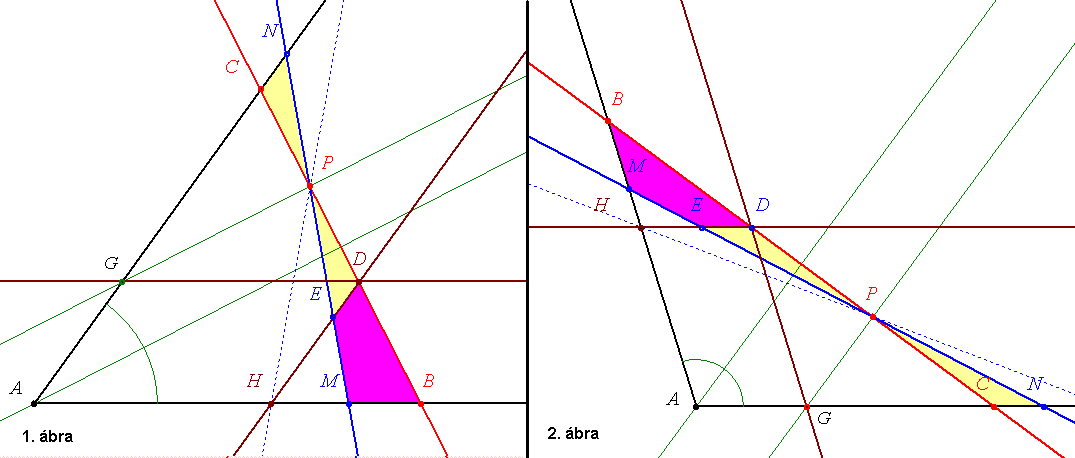
 B. 3847 feladathoz: Feltehetjük, hogy 180o-nál kisebb szögről van szó, mert különben az egyenes nem vághat ki  -t a szögtartományból. -t a szögtartományból.
Húzzuk meg a szögfelezőt. Könnyen belátható, hogy, ha az adott P pont a szögfelezőn van akkor a P pontban a szögfelezőre állított merőleges egyenes vágja le a szögtartományból a legkisebb területű  -t. -t.
Ha P nincs a szögfelezőn akkor húzzunk rajta keresztül merőlegest és párhuzamost a szügfelezővel! A merőleges a szögszárakat B-ben és C-ben, a párhuzamos G-ben metszi.
Húzzunk G ponton át párhuzamost a másik szögszárral, ennek BC-vel alkotott metszéspontja legyen D pont. Majd D ponton át párhuzamost AG szögszárral ennek metszéspontja AB-vel legyen H pont.
Legyen M a BH szakasz egy belső pontja és N az MP egyenes metszéspontja a másik szögszárral, E pont pedig MP és DH egyenesek metszéspontja.
Mivel PC=PD és CN párhuzamos ED, ezért 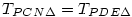
Mozogjon az M pont a szögszáron a B ponttól a H pont felé. Ekkor at AMN területe csökken ABC területe csökken ABC területéhez képest, méghozzá BDEM négyszög területével. Egészen addig míg H pontba érünt. Az AMN területéhez képest, méghozzá BDEM négyszög területével. Egészen addig míg H pontba érünt. Az AMN területe ekkor lesz a legkisebb, hiszen M ponttal tovább haladva A felé a PMH területe ekkor lesz a legkisebb, hiszen M ponttal tovább haladva A felé a PMH területe kisebb mint a P pont másik oldalán a szögszárig terjedő háromszög területe. területe kisebb mint a P pont másik oldalán a szögszárig terjedő háromszög területe.
Tehát a keresett egyenes a PH.
|
 |
|
|
| [98] rizsesz | 2005-08-25 23:43:04 |
 Tök jó, én vagyok Sherlock, nézd meg a feladat statisztikájánál, amit a feladatoknál olvashatsz el (simán klikk a fizika feladatokra) :)
|
|
|
|
| [94] Hardre | 2005-08-24 19:03:14 |
 Ha valaki meg tudta rendesen csinálni a P. 3811. feladatot, írja le pls hogy, mert én elakadtam.
Mégpedig ott, hogy a mágneses térbe ér a részecske. Felírtam a rá ható erőket, felbontottam komponensekre, de csak az éppen megtett út/sebesség/idő függvényében. Ha a megtett utat veszem változónak, akkor az a baj, hogy y(x) függvény általános ívhosszára olyan képlet van, amit itt sztem nem érdemes felhasználni. Akárhogy írom fel; a gond mindig a pálya függvényének meghatározása. Hiába tudom a 2 komponensének 2. deriváltját, abból túl bonyolult dolgok jönnek ki, mert sztem van vmi amire nem jöttem eddig rá.
|
|
|
|
| [90] Szabó Dani | 2005-03-10 14:44:53 |
 Valaki tegye fel a P. 3754. feladat megoldását!
|
|
| [89] rizs | 2005-03-09 14:46:40 |
 hát,a 2 egyenlet összegét rendezve csupa teljes négyzet jön ki, és onnan x=2, y=3.
|
|
| [88] jenei.attila | 2005-03-09 13:51:09 |
 Oldjuk meg a Lórántfy által kitűzött B.3790 feladatot. Nekem van egy megoldásom, kíváncsi vagyok, ti hogy oldjátok meg.
|
|
| [87] Káli gúla | 2005-03-06 19:08:40 |
 Kedves Balázs!
Elküldtem mailben azokat az oldalakat a Matematikai Lapokból, amik a feladathoz kapcsolódnak. A téglás pakolásokról az interneten is találhatsz cikkeket:
http://www-math.mit.edu/~rstan/transparencies/tilings.pdf
http://www.math.uni-bielefeld.de/~sillke/POLYCUBE/PROOF/deBruijn/filling-boxes-with-bricks.pdf
http://www.mrlonline.org/mrl/1994-001-005/1994-001-005-003.pdf
http://www.combinatorics.org/Volume_4/PDF/v4i2r12.pdf
|
| Előzmény: [86] Strenner Balázs, 2005-03-05 21:14:06 |
|
| [86] Strenner Balázs | 2005-03-05 21:14:06 |
 Hello!
Nagyon szép a megoldás, sokkal általánosabb, mint a feladat. Én is hasonló dolgokkal próbálkoztam: vetületekkel, csak nem tudtam elszakadni a kockától, de ez a szétszeletelés nagyon leleményes. Érdekelne az a Kömal-cikk, amiben ezzel foglalkoznak, de nem találtam meg. Biztos, hogy jó az év?
|
| Előzmény: [85] Káli gúla, 2005-02-27 21:48:19 |
|
| [85] Káli gúla | 2005-02-27 21:48:19 |
 Hello!
Legyen a1,...,an N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i n, amire ai|bi. n, amire ai|bi.
Bizonyítás indukcióval. n=1-re az állítás igaz. Tegyük fel, hogy an nem osztója bn-nek. Legyen L a B téglának az n-edik tengelyre merőleges alsó lapja, ez tehát egy b1,...,bn-1 élhosszúságú, n-1 dimenziós tégla. Elég belátni, hogy L-ben maradva is minden lámpát át lehet állítani, ekkor ugyanis az indukciós feltevés szerint ai|bi-nek kell teljesülni valamilyen i n-1-re. Tekintsük B-ben az L-lel párhuzamos bn db réteg közül azokat, amiknek a távolsága L-től n-1-re. Tekintsük B-ben az L-lel párhuzamos bn db réteg közül azokat, amiknek a távolsága L-től  0 (mod an) vagy 0 (mod an) vagy  -1 (mod an). Szorítkozzunk a B kivilágításánál használt csíkok közül azokra, amiket ezek a rétegek tartalmaznak, és vegyük ezeknek a csíkoknak az L-re eső vetületeit (eltoltjait). Belátjuk, hogy minden x -1 (mod an). Szorítkozzunk a B kivilágításánál használt csíkok közül azokra, amiket ezek a rétegek tartalmaznak, és vegyük ezeknek a csíkoknak az L-re eső vetületeit (eltoltjait). Belátjuk, hogy minden x L-beli pontot páratlan sok vetületi csík fog fedni. an nem osztja bn miatt a 0 maradékosztályban eggyel több réteg van, mint a (-1) maradékosztályban, azaz a tekintett rétegek száma páratlan, az ide eső, x feletti pontok B-beli multiplicitása is páratlan volt, így ezen pontok multiplicitásainak összege páratlan. Az összegből el kell hagyni az L-re merőleges, an hosszúságú csíkokat, de ezek mind pontosan két x feletti pontot tartalmaznak, ezért a paritás továbbra is páratlan marad. L-beli pontot páratlan sok vetületi csík fog fedni. an nem osztja bn miatt a 0 maradékosztályban eggyel több réteg van, mint a (-1) maradékosztályban, azaz a tekintett rétegek száma páratlan, az ide eső, x feletti pontok B-beli multiplicitása is páratlan volt, így ezen pontok multiplicitásainak összege páratlan. Az összegből el kell hagyni az L-re merőleges, an hosszúságú csíkokat, de ezek mind pontosan két x feletti pontot tartalmaznak, ezért a paritás továbbra is páratlan marad.
(1) A feladatra a nemleges válasz egyszerűen következik, mert a 2x2x2-es kockákat az x1, a 3x3x3-asakat a x2, a 7x7x7-eseket az x3 tengellyel párhuzamos csíkokra bonthatnánk, és a 2005 egyik hosszal sem osztható.
(2) A feladathoz ugyan nem kell, de a csíkok nemcsak B részhalmazai lehetnek. A bizonyításban semmi újat nem kell mondani.
(3) Ehhez hasonló feladat jelent meg a Matematikai Lapok Feladatrovatában (1962/3-4, pp 314-317.), a fenti gondolatmenet is az ottani egyik megoldás mintájára készült. A kérdéskör állítólag úgy jött elő, hogy N. G. De Bruijn 7 éves kisfia megfigyelte, hogy 1x2x4-es téglákkal nem lehet egy 6x6x6-os ládát kitölteni.
|
| Előzmény: [84] SAMBUCA, 2005-02-22 03:32:47 |
|
| [84] SAMBUCA | 2005-02-22 03:32:47 |
 Na hell!
Ha vakinek van megoldása az A.363.-ra akkor beírhatná. Nagyon kiváncsi lennék...
SAMBUCA
|
|





 -mg=0
-mg=0

 3,8 cm.
3,8 cm.

 mn-1xn-1
mn-1xn-1  yi, de minden i-nél nagyobb és n-1 -nél kisebb-egyenlő j indexre xj<yj, és legyen
yi, de minden i-nél nagyobb és n-1 -nél kisebb-egyenlő j indexre xj<yj, és legyen  -t a szögtartományból.
-t a szögtartományból. 



 N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i
N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i 0 (mod an) vagy
0 (mod an) vagy 