| [754] w | 2013-02-16 21:54:33 |
 A.573. Legyen D={0,1,2,...,9} a számjegyek halmaza, és R D×D rendezett számjegypárok egy halmaza. Azt mondjuk, hogy egy (a1,a2,a3,...) végtelen számjegysorozat kompatibilis R-rel, ha (aj,aj+1) D×D rendezett számjegypárok egy halmaza. Azt mondjuk, hogy egy (a1,a2,a3,...) végtelen számjegysorozat kompatibilis R-rel, ha (aj,aj+1) R minden j pozitív egészre. Határozzuk meg a legkisebb olyan K pozitív egészt, amire igaz, hogy ha egy tetszőleges R R minden j pozitív egészre. Határozzuk meg a legkisebb olyan K pozitív egészt, amire igaz, hogy ha egy tetszőleges R D×D halmaz legalább K különböző számjegysorozattal kompatibilis, akkor R végtelen sok számjegysorozattal kompatibilis. D×D halmaz legalább K különböző számjegysorozattal kompatibilis, akkor R végtelen sok számjegysorozattal kompatibilis.
Megoldásvázlat. Keressük azt a K számot, melyre lesz végtelen sok számjegysorozat, ami megfelel a feltételeknek, azonban (K-1)-re ezt már nem mondhatjuk biztosan. Így K-1 a sorozatok számának véges maximuma. A továbbiakban feltesszük, hogy a sorozatok száma véges.
Vegyünk egy olyan gráfot, melynek csúcsai D elemeit (a számjegyeket) jelentik, a csúcsokat irányítot szakaszok kötik össze, ezzel jelképezve az R halmaz rendezett párjait (az irány a pár első tagjából a másodikba mutat, egy csúcs önmagába is irányíthat). A végtelen sorozatnak az felel meg, hogy egy adott csúcsból indulva, a "nyilaknak" megfelelően utazva végtelen sokáig tekereghetünk a gráfban.
Első lépésben azt látjuk be, hogy a végtelen számjegysorozat periodikus. A sorozatban lesz végtelen sokszor fellépő azonos d számjegy (skatulyaelv), tekitsük az első hármat, ami a sorozatban előfordul. Ha ezek között más-más számjegysor szerepel, akkor végtelen sok sorozat lehetne, mert két módon is eljuthatunk a d-ből önmagába (a szorzási szabállyal 2.2....= sorozat lehetne). Ugyanez elmondható a második háromra stb., a sorozat periodikus. Hasonlóan igazolhatjuk, hogy ez a periódus legfeljebb 10 számjegyet tartalmaz. sorozat lehetne). Ugyanez elmondható a második háromra stb., a sorozat periodikus. Hasonlóan igazolhatjuk, hogy ez a periódus legfeljebb 10 számjegyet tartalmaz.
Ezután az R-t jelentő gráfban végzünk maximalizáló operációkat. Ki-ki lássa be, hogy valóban ezek optimalizálják a gráfhoz tartozó K(R) számot; a végső gráftól eltérő gráf esetén mindig végezhetünk ilyen operációt. Megvizsgáljuk a gráf részeit. A végtelen sorozat periódusainak megfelelő körök lesznek (1.), ezekbe más csúcsok irányítanak (akár közvetetten is) (2.), továbbá vannak olyan csúcsok is, amelyek semelyik körhöz sem kapcsolódnak (3.). Először minden kört összekapcsolunk nyakláncszerűen egy körré. A (3.) csúcsokat irányítsuk a körbe. Láthatjuk, hogy K(R) akkor is növekszik, ha ezeket egy (2.) típusú résszé olvasztjuk össze. Azaz, olyan gráfot kaptunk, ami csak egy-egy (2.) és (1.) típusú részt tartalmaz. Végül láthatóvá válik, hogy akkor a legjobb, ha R={(0,1);(0,2);...;(0,9);(1,2);(1,3);...;(1,9);...;(9,9)}, és ekkor K=29+1=513.
|
|
| [753] w | 2013-02-15 21:27:02 |
 Nem raktak az A.578. feladatra megoldást, úgyhogy ha lehet, megkérném a Fórumozókat, hogy segítsenek megoldást találni.
Nekem az (a) rész sikerült (illetve hátramaradt, hogy P(n) nem nulla). Szorozzuk össze képzeletben a zárójeleket. Vizsgáljuk meg azokat a kapott tagokat, amelyben 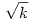 ak-szor szerepel. Ha ak-szor szerepel. Ha  ak páros, akkor a kapott tag egész lesz, ne foglalkozzunk ezekkel a tagokkal (még). Legyen tehát valamely ak páratlan. Tekintsük a zárójeleknek olyan egyértelmű párosítását, melyre egy zárójelpár minden tagjának ellentétes előjele van, kivéve ak páros, akkor a kapott tag egész lesz, ne foglalkozzunk ezekkel a tagokkal (még). Legyen tehát valamely ak páratlan. Tekintsük a zárójeleknek olyan egyértelmű párosítását, melyre egy zárójelpár minden tagjának ellentétes előjele van, kivéve 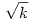 -nak (pl. n=4, k=2 esetén egy ilyen pár: -nak (pl. n=4, k=2 esetén egy ilyen pár: 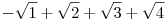 és és 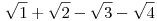 ). Vizsgáljuk meg, hogy egy-egy tag melyik zárójelekből melyik számokból szorzódhatott össze (tehát egy lehetséges szorzótényező-választást figyelünk meg), és minden zárójel helyett a zárójel ily módon megadott párjából válasszuk a megegyező abszolútértékű számot. Ekkor ak paritása miatt az eredetivel ellentétes előjelű lesz a kapott tag. Tehát ezzel bemutattunk egy bijekciót a kétféle előjelű megfelelő tagokból, ezért "kiejtik" egymást. Innen P(n) egész szám. ). Vizsgáljuk meg, hogy egy-egy tag melyik zárójelekből melyik számokból szorzódhatott össze (tehát egy lehetséges szorzótényező-választást figyelünk meg), és minden zárójel helyett a zárójel ily módon megadott párjából válasszuk a megegyező abszolútértékű számot. Ekkor ak paritása miatt az eredetivel ellentétes előjelű lesz a kapott tag. Tehát ezzel bemutattunk egy bijekciót a kétféle előjelű megfelelő tagokból, ezért "kiejtik" egymást. Innen P(n) egész szám.
Ha valaki tud mondani a (b) részre egy jó számolást, azt nagyon megköszönném. A P(n)>0 állítás bizonyítása talán a többi keletkezett tag megszámolásában rejlik.
|
|
| [752] w | 2013-02-15 20:17:41 |
 Azt értettem a korábbi hozzászólásom alatt, hogy a feladatot már korábban kitűzték általánosítva, így a januári feladat megoldását kitartó böngészéssel is meg lehetett volna találni... Persze a feladat 6-7. osztályos versenyfeladat-szint, úgyhogy mire kikeressük a feladatot, addigra 15-ször megoldhatnánk :-) Teljesen igazad van.
|
| Előzmény: [749] rizsesz, 2013-02-14 11:27:25 |
|
|
| [750] Róbert Gida | 2013-02-14 21:32:45 |
 Igen, ez egyszerűbb, mert nem kell hozzá végtelen sok prím létezése.
Harmadik bizonyítás: legyen a(n)=3*22n, ha n>0. Legyen néhány ilyen összege s, és ak a legkisebb benne, ekkor könnyen látható, hogy s=22k*(4*t+3). Így ha s teljes hatvány, akkor szükségképpen négyzetszám is (mert 2 kitevője s-ben 2 hatvány), de akkor 4*t+3 is, ellentmondás.
|
| Előzmény: [747] Fálesz Mihály, 2013-02-14 06:38:32 |
|
| [749] rizsesz | 2013-02-14 11:27:25 |
 Ennel kicsit rovidebb azert az, hogy a 11-gyel oszthatosag elbol 7 lehetseges esetre redukal (33-99). Konnyeden kiesik a 44 es a 66, azert, mert 6-ra vegzodo negyzetszamok, tehat utolso elotti jegyuk paratlan, a 33, 55, 77 es 99 pedig azert, mert utolso elotti jegyuk paros.
|
| Előzmény: [745] w, 2013-02-13 19:13:33 |
|
|
| [747] Fálesz Mihály | 2013-02-14 06:38:32 |
 A 2.6n alakú számokat is választhatjuk.
Ha n1<...<nk, akkor S=2.6n1+...+2.6nk=2n1+1.3n1(1+6n2-n1+...+6nk-n1) prímtényezős felbontásában a 2 és a 3 kitevője n1+1, illetve n1, ezek relatív prímek, tehát S nem lehet teljes hatvány.
|
| Előzmény: [746] Róbert Gida, 2013-02-13 20:25:50 |
|
| [746] Róbert Gida | 2013-02-13 20:25:50 |
 Legyen p(n) az n-edik prím, és 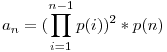 . Ekkor, ha véges sokat választasz ki közülük, és k-adik indexű a legkisebb kiválasztott, akkor az összeg osztható lesz p(k)-val, mert mindegyik tag osztható azzal, de pk2-tel már nem osztható (ak-n kívül minden tag osztható vele, csak ak nem), így az összeg nem lehet teljes hatvány. . Ekkor, ha véges sokat választasz ki közülük, és k-adik indexű a legkisebb kiválasztott, akkor az összeg osztható lesz p(k)-val, mert mindegyik tag osztható azzal, de pk2-tel már nem osztható (ak-n kívül minden tag osztható vele, csak ak nem), így az összeg nem lehet teljes hatvány.
|
| Előzmény: [744] w, 2013-02-13 17:31:30 |
|
| [745] w | 2013-02-13 19:13:33 |
 A B.4503 megoldásához ennyit: B.4216 ;-)
|
|
| [744] w | 2013-02-13 17:31:30 |
 Létezik-e olyan pozitív egészekből álló végtelen sorozat, melyből véges sokat kiválasztva, a számok összege nem lesz nk alakú (k>1, n egész számok)?
Kvant
|
|
|
| [742] w | 2013-02-10 22:04:12 |
 Elég lett volna annyit írni: tetszőleges a, b egészekre a2-b2=(a+b)(a-b), a szorzat tényezői azonos paritásúak, így ha az páros, akkor 4-gyel osztható (számelmélet alaptétele). Továbbá a=k+1, b=k választással a2-b2=(k+1+k)(k+1-k)=2k+1, illetve a=k+1, b=k-1 választás a2-b2=(k+1+k-1)(k+1-k+1)=4k-t gyárt, ahol k tetszőleges egész; kész vagyunk.
|
| Előzmény: [741] w, 2013-02-10 22:03:13 |
|
| [741] w | 2013-02-10 22:03:13 |
 C.1145. megoldásából: "Írjuk fel két tetszőleges négyzetszám különbségét. Ez valahány egymás utáni négyzetszám összege lesz: ..."
(Egy kis elírás van a megoldás leírásában.)
|
| Előzmény: [737] Kós Géza, 2013-01-15 23:25:28 |
|
| [740] w | 2013-02-10 21:53:12 |
 Köszönöm a segítséget. A feladaton sokat gondolkozgattam decemberben, de nem sikerült megoldani, korán feladtam. Amit mondtál, addig kb. eljutottam... Örülök, hogy a megoldást most a honlapra is felrakták :)
|
| Előzmény: [739] m2mm, 2013-02-09 01:23:30 |
|
| [739] m2mm | 2013-02-09 01:23:30 |
 A.576.
segítség 1: Először próbáld megoldani szabályos n-szögre ci=1, t=0 esetén. Ezután próbáld a gondolatmenetet továbbvinni az általános feladatra.
segítség 2: Csak irányítástartó hasonlóságok kellenek.
|
| Előzmény: [738] w, 2013-01-31 19:10:41 |
|
| [738] w | 2013-01-31 19:10:41 |
 Ha valaki írna a decemberi A-példák valamelyikére megoldást, azt nagyon megköszönném.
|
|
|
|
| [735] Róbert Gida | 2013-01-15 21:40:49 |
 K.357 "Az 5 többszöröseinek utolsó számjegye 0 vagy 5 lehet, ennél eggyel kisebb számé 9 vagy 4."
A 0-t is az 5 többszörösének veszik, és az eggyel kisebb -1 utolsó jegye 1. És ez még mindig a hibákkal teli decemberi lapszámos feladat. Sok időt nem fordíthatnak a megoldások útmutatójára.
Hat pontból adnék azért 1 pontot a megoldásra.
|
|
| [734] Róbert Gida | 2013-01-15 21:28:38 |
 Decemberi lejárt B4500.: "Útmutatás: Igen. Bizonyítsuk be, hogy f(1)=1."
Bizonyítást nem találunk hozzá, de mindegy is, mert nem igaz: legyen g(n)=2*n2+2*n-1. Ekkor g(1)=3; és megfelelő polinom!
Prímek meg egyáltalán nem kellenek a bizonyításhoz, elég azt belátni, hogy fi(n) 1mod n, illetve nálam: gi(n) 1mod n, illetve nálam: gi(n) -1mod n. -1mod n.
|
|
| [733] w | 2012-12-16 18:00:47 |
 Úgy tűnik, hogy nem fogják a honlapra felrakni az A. 573. feladat megoldását, pedig relatívan egyszerű volt (a leírása a legnehezebb rész).
Valaki elmondaná-e az A. 572. megoldását?
|
|
|
| [731] vogel | 2012-11-26 02:25:13 |
 Ezek az útmutatások, amik a megoldások felett vannak, megjelennek az újságban is?
|
|
| [730] w | 2012-11-24 23:41:27 |
 A honlapinál egyszerűbb megoldás B.4477-re:
A feltétel szerint A és B rajta van a PQ Apollóniusz-körén; Thálesz-tétel megfordítása szerint R is rajta van. A PRQ< szögfelezője messe PQ-t A'-ben -- szögfelezőtétel miatt A'=A, innen adódik a bizonyítandó állítás. (Nem töltök fel ábrát, mert könnyű fejben elképzelni.)
Nagyon szépen, egyszerűen kijön C.1139. (Legalább mekkora átfogójú az a derékszögű háromszög, amelynek kerülete k?):
A szokásos jelölésekkel 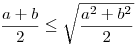 , azaz , azaz  , innen , innen 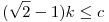 , ezzel készen is vagyunk, mert egyenlőség a=b esetén fennállhat. , ezzel készen is vagyunk, mert egyenlőség a=b esetén fennállhat.
|
|


 D×D rendezett számjegypárok egy halmaza. Azt mondjuk, hogy egy (a1,a2,a3,...) végtelen számjegysorozat kompatibilis R-rel, ha (aj,aj+1)
D×D rendezett számjegypárok egy halmaza. Azt mondjuk, hogy egy (a1,a2,a3,...) végtelen számjegysorozat kompatibilis R-rel, ha (aj,aj+1) R minden j pozitív egészre. Határozzuk meg a legkisebb olyan K pozitív egészt, amire igaz, hogy ha egy tetszőleges R
R minden j pozitív egészre. Határozzuk meg a legkisebb olyan K pozitív egészt, amire igaz, hogy ha egy tetszőleges R sorozat lehetne). Ugyanez elmondható a második háromra stb., a sorozat periodikus. Hasonlóan igazolhatjuk, hogy ez a periódus legfeljebb 10 számjegyet tartalmaz.
sorozat lehetne). Ugyanez elmondható a második háromra stb., a sorozat periodikus. Hasonlóan igazolhatjuk, hogy ez a periódus legfeljebb 10 számjegyet tartalmaz.  ak páros, akkor a kapott tag egész lesz, ne foglalkozzunk ezekkel a tagokkal (még). Legyen tehát valamely ak páratlan. Tekintsük a zárójeleknek olyan egyértelmű párosítását, melyre egy zárójelpár minden tagjának ellentétes előjele van, kivéve
ak páros, akkor a kapott tag egész lesz, ne foglalkozzunk ezekkel a tagokkal (még). Legyen tehát valamely ak páratlan. Tekintsük a zárójeleknek olyan egyértelmű párosítását, melyre egy zárójelpár minden tagjának ellentétes előjele van, kivéve 

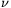 ) meg a
) meg a 

 1 (amit persze lehet egyszerűbben is mondani), és ez elég is.
1 (amit persze lehet egyszerűbben is mondani), és ez elég is.  1mod n, illetve nálam: gi(n)
1mod n, illetve nálam: gi(n)