| [102] Gubbubu | 2004-01-29 01:37:28 |
 Kedves Csimby!
Gratulálok! Ezt gyorsan összehoztad!
Ennek alapján tetszőleges p>5 prímre is létezik végtelen sok különböző n,k természetes szám úgy, hogy p|f(n)-f(k) legyen.
Sőt, ha A>1 tetszőleges szám, akkor bármely p>A prímhez (ekkor biztosan (A,p)=(d,p)=1 , A minden d osztójára), létezik végtelen sok olyan különböző n,k természetes szám, hogy
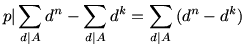
teljesüljön. Szerintem ezt már nem lenne olyan egyszerű belátni, ha valaki nem ismerné az előzményeket....
|
| Előzmény: [101] Csimby, 2004-01-28 22:58:26 |
|
| [101] Csimby | 2004-01-28 22:58:26 |
 30.feladat
1237prím a1236 a1236 1 1
f(n+1236)=2n+1236+3n+1236+5n+1236 2n+3n+5n=f(n). 2n+3n+5n=f(n).
Tehát f(n) és f(n+1236) ugyan annyi maradékot ad 1237-tel osztva, tehát tényleg végtelen sok megoldás van!
|
|
| [100] Csimby | 2004-01-28 22:20:18 |
 A 30. feladathoz Ha n,k <100 akkor a következő n,k számpárok jók: (94,12) (63,25) (96,27)
1000-ig 419 db megfelelő számpár van, 2000-ig 2377 db, 3000-ig 5966 db, 4000-ig 11153 db, A sejtés tehát az, hogy végtelen sok megoldás van.
|
|
| [99] Gubbubu | 2004-01-28 21:47:45 |
 Kedves Csimby!
Közben rájöttem én is, hogy szokásom szerint elhamarkodtam a dolgot! Rossz az egész! Hiába, öregszem... bocs!
Rajzolgattam egy pár grafikont, és rájöttem, hogy a feladat nehezebb, mint gondoltam!
Tehát, bár a "Suhanc 4." feladat megoldott, de adott helyette a a következő (amit most nem tudok, hogy ujjgyakorlat-e):
30. feladat:
Igazoljuk, hogy f(n):=2n+3n+5n esetén nincsenek olyan különböző n,k N számok, melyekre 1237|f(n)-f(k) (vagy igazoljuk az ellenkezőjét...)! N számok, melyekre 1237|f(n)-f(k) (vagy igazoljuk az ellenkezőjét...)!
Azt hiszem, egyébként az általam készített táblázat nem is igen fog segíteni a megoldásban. De nem baj, olyan szépen mutat, és ez az első TeX-ben készített táblázatom...
Üdv mindenkinek: G. Most pedig megyek, napolajat teszek a képemre...
|
| Előzmény: [98] Csimby, 2004-01-28 21:15:41 |
|
| [98] Csimby | 2004-01-28 21:15:41 |
 Kedves Gubbubu: Nem csak a 7-re végződő számok oszthatóak 1237-tel, te is írtad az n=k esetet ahol a különbség 0 (nem 7-re végződik, de megfelel).
"Vagyis 1237 csak úgy lehet f(n)-f(k), ha f(k)=3. " Nem csak 1237 lehet a különbség, hanem k*1237.
De az is lehet, hogy valamit félreértettem...
|
|
| [97] Gubbubu | 2004-01-28 19:07:29 |
 Kedves Fórum!
Megoldást küldöm Suhanc első "elfeledett" feladataira:
"Suhanc 4." fa. megoldása:
Természetesen 1237|(2n+3n+5n)-(2k+3k+5k)=0 bármely n,k N,n=k-ra. Lehet pl. n=2. N,n=k-ra. Lehet pl. n=2.
Na jó, ez így túl könnyű volt. Kössük ki, hogy n>k (ez az általánosság megszorítása nélkül kiköthető, az n<k esetben ugyanis a hatványösszegek különbségei egymás ellentettjei lesznek, így az n>k párra ennek épp akkor osztója bármi, még az 1237 is, ha az n<k osztója.
Legyen f(n):=2n+3n+5n, és tekintsük a következő táblázatot, mely oszlopai sorra n-t, 2n-t mod 10, 3n-t mod 10, 5n-t mod 10, végül f(n)-t mod 10 tartalmazzák (vagyis e mennyiségek utolsó számjegyét:
| n |
2n |
3n |
5n |
f(n) |
| 0 |
1 |
1 |
1 |
3 |
| 1 |
2 |
3 |
5 |
0 |
| 2 |
4 |
9 |
5 |
8 |
| 3 |
8 |
7 |
5 |
0 |
| 4 |
6 |
1 |
5 |
2 |
| 5 |
2 |
3 |
5 |
0 |
| 6 |
4 |
9 |
5 |
8 |
| ... |
... |
... |
... |
... |
|
Látható, de könnyen be is látható (akár kongruenciákkal számolva, akár a tízes számrendszerben számjegyeket szorozgatva), hogy a táblázat periodikus, az n=1-től kezdve a 4 legkisebb periódussal.
Tehát f(n)-f(k) mod(10) számolva a 3-0=3, 3-8=-5=5, 3-2=1, 0-3=7, 0-0=0, 0-8=2, 0-2=8, 8-3=5, 8-0=8, 8-8=0, 8-2=6, 2-3=9, 2-0=2, 2-8=4, 2-2=0 értékeket veheti fel. A fenti felsorolásból láthatóan nem sokszor kapunk 7-et, úgy lehet csak f(n)-f(k) 7 mod(10), ha k=1. Vagyis 1237 csak úgy lehet f(n)-f(k), ha f(k)=3.
1237=f(n)-3;
1240=f(n); Ez az egyenlet pedig nem megoldható. n=5 már túl sok (több mint 3000 f(n) értéke, mivel 55=3125, n=4 pedig túl kevés, f(n)=722. Vagyis ha n és k különbözőek, akkor nincs megoldás. Az egyetlen megoldás n=k.
Nemsokára felteszem a másik "elfeledett" feladat megoldását is. G.
|
| Előzmény: [92] Suhanc, 2004-01-24 10:05:31 |
|
|
|
|
| [93] lorantfy | 2004-01-24 11:11:26 |
 Kedves Fórumosok
Valóban Suhanc 4. és 5. feladata feledésbe merült. Ebben én is hibás vagyok, mert véletlenül felülszámoztam.
A megoldatlan feladatok listája ebben a témában:
4. 5. [6]
6. [18]
13. [48]
16 [53]
18.b [69]
22. [77]
24. [81]
27. [86]
29. [92]
Kérek minden feladatkitűzőt, hogy feladatát (lehetőleg félkövér kiemeléssel) számozza és a megoldókat pedig arra, hogy hivatkozzanak a feladatszámra! Köszönettel: L.
|
| Előzmény: [90] Gubbubu, 2004-01-24 09:04:36 |
|
| [92] Suhanc | 2004-01-24 10:05:31 |
 Kedves Gubbubu!
De, tényleg ez volt a feladat...odaírtam mellé, hogy ez villámkérdés...igazából annak is elég rövidke...:)
Ezen a szakörön legutóbb találkoztam egy egyszerű, de nagyon aranyos feladattal; "ohne nehézség" felkiáltással leírom:
29. feladat
Legyenek a;b;c egy háromszög oldalai! Igazoljuk, hogy
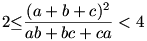
|
| Előzmény: [90] Gubbubu, 2004-01-24 09:04:36 |
|
| [91] Suhanc | 2004-01-24 09:42:13 |
 Kedves László!
Hát Igen! Ez valóban pár sorral rövidebb...;) Köszönöm!!:) Én általában szeretem az olyan geometriai feladatokat, amikről időközben kiderül, hgy lényegében nem is geometria... de azért túlzásokba nem szabad esni!!!;)
|
|
| [90] Gubbubu | 2004-01-24 09:04:36 |
 Kedves Suhanc!
[6] hozzászólásodban szerepel két, azóta "elfeledett", pedig elég érdekes feladat. A második főként trükkös és jópofa, de az elsőt nem egészen értem. "Tekintve 2,3,5 n-edik hatványainak összegét, van két szám, amelynek különbsége osztható 1237-tel". Gondolom, nem arról van szó, hogy keressünk olyan n,k számokat, melyekre 1237|(2n+3n+5n)-(2k+3k+5k), mivel ez még ujjgyakorlatnak is túl egyszerű lenne. Miről van szó pontosabban?
Üdv: G.
|
| Előzmény: [6] Suhanc, 2003-11-26 18:24:56 |
|
|
| [88] Suhanc | 2004-01-23 22:46:07 |
 Kedves Károly!
A feladatodra van egy megoldásom, de eléggé ronda (ágyúval galambra...) ha nem kerül föl más megoldás, feltennéd a tiédet? (azt is megköszönöm, ha mailben elküldöd).
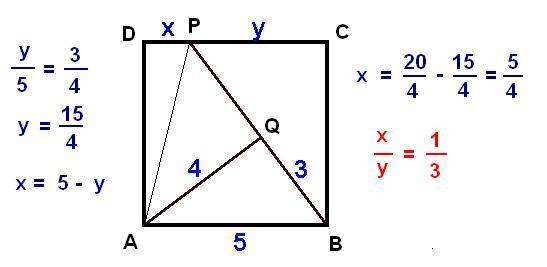
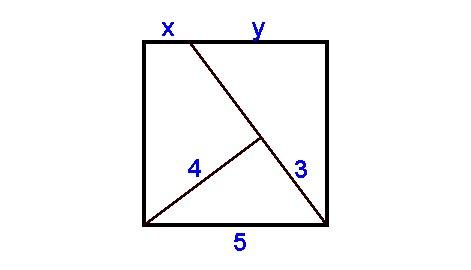
M: (sajnos, az ábraszerkesztéssel nem vagyok megbarátkozva) Legyenek a négyzet csúcsai A;B;C;D pontok, úgy, hogy A legyen az ábra bal alsó sarkában (óramutató járásaval ellentétesen betűzve). x és y szakaszok közös pontja legyen P, a 3 és 4 egységnyi szakaszok közös pontja legyen Q.
ADP és APQ háromszögek derékszögűek; a Pitagorasz-tétel szerint: 25+x2=z2+16
Ebből: 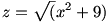
PBC derékszögű háromszögre felírva a Pitagorasz-tételt: 
Négyzetre emelve: 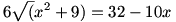
Tovább bontogatva a 16x2-160x+175=0 egyenletet kapjuk, melynek megoldásai X1=35/4;eznyilvánnemmegoldás,mertX<5;ésX2=5/4. Ekkor y=15/4 , tehát x/y=1/3 .
|
|
| [87] Hajba Károly | 2004-01-20 09:45:35 |
 Egy kis szösszenet
28. feladat:
Mennyi x:y aránya az 5*5 négyzet esetén?
|
 |
|
|
| [85] Gubbubu | 2004-01-19 12:32:59 |
 Kedves Lészló!
Valóban, az alap oldalainak szögei meg kell hogy egyezzenek, ezt elfelejtettem mondani.
Tetszik a vektorok használata. Erre nem is gondoltam.
Az átdarabolásos bizonyítás úgy menne, hogy először egy háromszög alapú ferde, majd egy ugyanekkora (egybevágó) háromszög alapú, de egyenes hasábot levágunk a p.p. egyik végéről és tesszük a másik végére. Megpróbálom majd lerajzolni.
Üdv.:G.
|
| Előzmény: [83] lorantfy, 2004-01-18 21:30:16 |
|
| [84] lorantfy | 2004-01-19 11:16:34 |
 26. feladat megoldása: Tompaszögű háromszög esetén: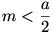
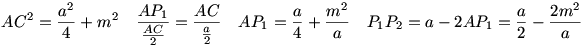
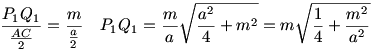
Derékszögű háromszög esetén: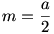
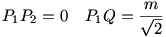
Tompaszögű háromszög esetén: 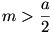
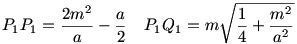
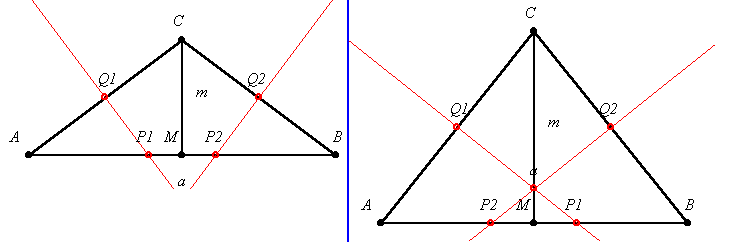
A feladat szövege szerint szigorú értelemben csak  =60o-ig van megoldás, ekkor P2=A, P1=B. Ennél kisebb csúcsszög esetén a P1 , P2 pontok az alapon kívül esnek. =60o-ig van megoldás, ekkor P2=A, P1=B. Ennél kisebb csúcsszög esetén a P1 , P2 pontok az alapon kívül esnek.
|
 |
| Előzmény: [82] Hajba Károly, 2004-01-16 14:14:19 |
|
| [83] lorantfy | 2004-01-18 21:30:16 |
 Kedves Gubbubu!
A feladat megfogalmazása kicsit pontatlan: Az alaplapon lévő szögeknek meg kell egyezni, a térfogatok csak akkor egyenlőek. Másrészt, ha az alap paralelogramma, akor a test már nem téglatest. De azért remélem jól értem a feladatot.
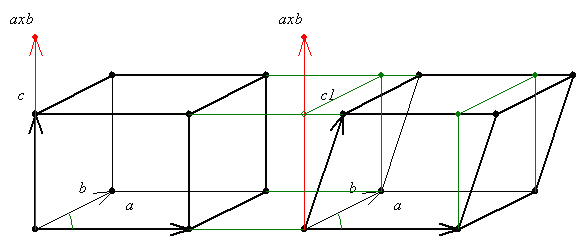
25. feladat megoldása: Természetesen átdarabolni is lehet, de egy kis változatosság nem árt: számoljuk a testek térfogatát a T=(axb).c vektor vegyesszorzattal.
Aki nem ismeri: axb vektoriális szorzat az a,b síkjára merőleges vektor, nagysága pedig absin , ami éppen a paralelogramma területe. Ezzel a vektorral skalárszorozva a c vektort kapjuk a test térfogatát. , ami éppen a paralelogramma területe. Ezzel a vektorral skalárszorozva a c vektort kapjuk a test térfogatát.
Látszik, hogy c1 vetülete axb-re éppen c, így a térfogatok egyenlőek.
|
 |
| Előzmény: [81] Gubbubu, 2004-01-15 01:17:11 |
|
| [82] Hajba Károly | 2004-01-16 14:14:19 |
 26. feladat
Vegyünk egy a alapú m magasságú egyenlő szárú háromszöget. Az alap P1 és P2 pontjából a szárak oldalfelező pontjaira (Q1,Q2) merőlegest tudunk állítani. Mennyi P1P2 ill. P1Q1 szakaszok hossza?
HK
|
|
| [81] Gubbubu | 2004-01-15 01:17:11 |
 Üdv;
Még két hasonló feladat: (nem nehezek, legalábbis az első, a másodikhoz kell egy kis térlátás)
24.feladat: Legyenenek az 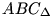 a,b oldalainak felezőpontjai F,G, súlyvonala S. Lássuk be, hogy az a,b oldalainak felezőpontjai F,G, súlyvonala S. Lássuk be, hogy az  és az és az 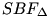 háromszögek végszerűen egyenlőek, azaz átdarabolhatóak egymásba, és adjunk meg egy konkrét átdarabolást is. háromszögek végszerűen egyenlőek, azaz átdarabolhatóak egymásba, és adjunk meg egy konkrét átdarabolást is.
25.feladat: Igazoljuk, hogy egy a,b,c oldalú, m testmagasságú paralelepipedon és egy a,b oldalú paraleogramma alapú, m magasságú téglatest térfogata megegyezik!
Segítség: persze át kellene darabolni a testeket...
|
|
| [80] Gubbubu | 2004-01-14 20:35:24 |
 Kedves R.B.!
Jól emlékszel, a tétel úgy szól, és valóban Bolyai F. tételének hívják. A bizonyítása tényleg nem túl nehéz, bár egy kissé hosszadalmas, szerintem nem illik ebbe a rovatba.
Én azonban, ha elvártam volna valamit, akkor az egy konkrétabb bizonyítás, mondjuk egy ábra lett volna. Persze nem vártam el semmit, még azt sem, hogy akadjon valaki, aki megoldja a feladatot és fölteszi a megoldást, csak azért tűztem ki, hátha valakinek kedve van ilyesmiken is gondolkodni, amikor fáradt egy nehezebb probléma megoldásához.
Üdv: G.
|
|
| [79] Rácz Béla | 2004-01-14 01:45:16 |
 Azt hiszem, tétel szól ennek a feladatnak az általánosabb formájáról, azaz hogy bármely két egyenlő területű sokszög véges sok vágással átdarabolható egymásba. Úgy emlékszem, hogy ezt Bolyai Farkas tételének is hívják. A bizonyításhoz nem kell igazán újító ötlet, úgyhogy akár ezt is meg lehetne itt kérdezni.
|
| Előzmény: [78] Gubbubu, 2004-01-14 00:55:24 |
|
| [78] Gubbubu | 2004-01-14 00:55:24 |
 Egy ujabb egyperces:
Lássuk be, hogy tetszőleges (nem elfajult) háromszög bármely súlyvonala a háromszöget két olyan részháromszögre osztja, amelyek végszerűen egyenlőek (azaz véges sok síkidomra vágással átdarabolhatóak egymásba)!
|
|




 a1236
a1236 1
1 N számok, melyekre 1237|f(n)-f(k) (vagy igazoljuk az ellenkezőjét...)!
N számok, melyekre 1237|f(n)-f(k) (vagy igazoljuk az ellenkezőjét...)! 

 -nek CGF
-nek CGF =
= .
. 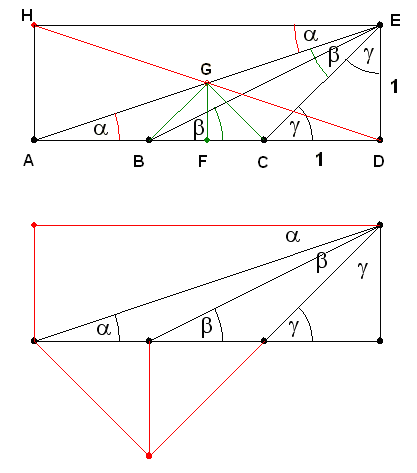

 +
+ a külsőszög-tétel miatt. Tehát a keresett öszzeg 2
a külsőszög-tétel miatt. Tehát a keresett öszzeg 2